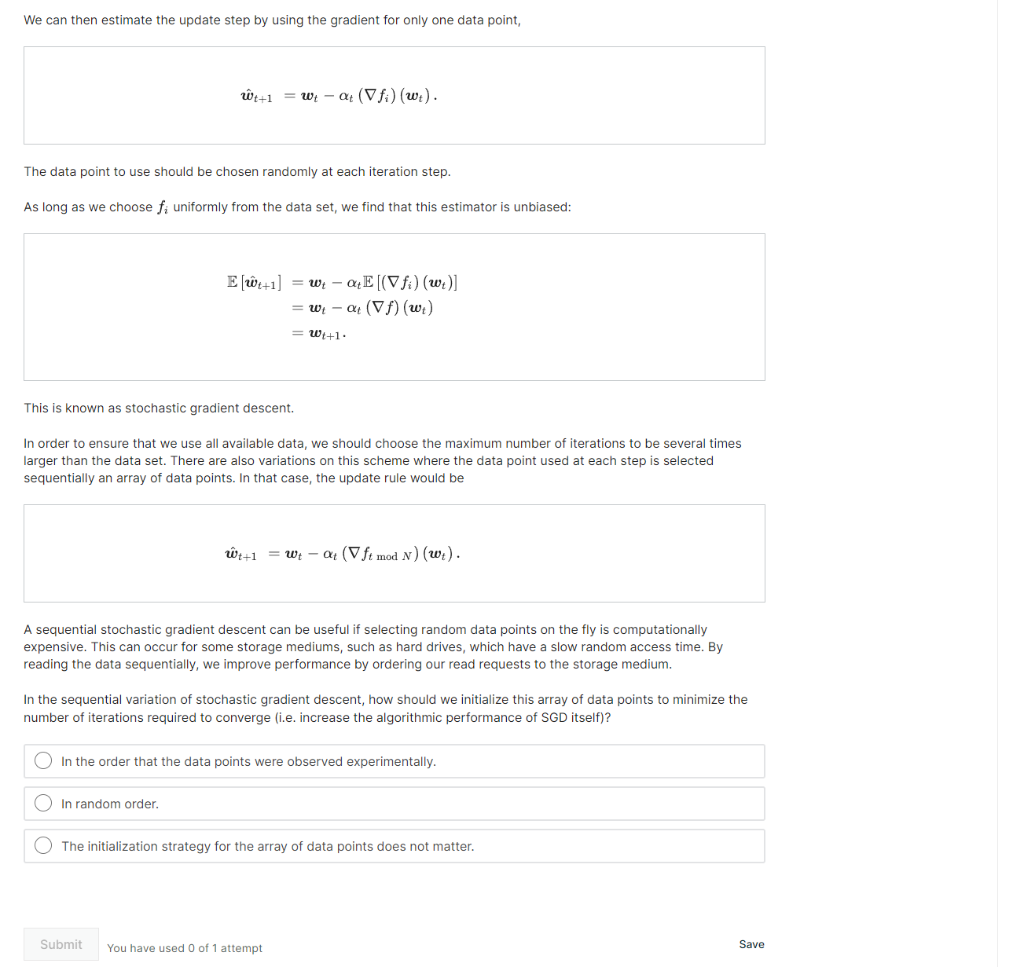
Stochastc gradient descent 1 point possible (graded) Even if we can fit a large data set in the memory of our computer, computing the gradient of f requires iterating over every data point. This can be a considerably lengthy process, and must be repeated often for each step in the gradient descent process. Instead, we seek to reduce the number of data points that are required for computing the gradient. We will do this by taking a subsample of the data. Notice that we can freely rescale the loss function by a multiplicative constant: f(w)f(w)=N1i=1Nfi(w) This looks a lot like a mean. Therefore, if we define our data set to be a population, then we can write the loss function as an expectation over this population: f(w)f(w)=E[fi(w)] We can then estimate the update step by using the gradient for only one data point, w^t+1=wtt(fi)(wt). The data point to use should be chosen randomly at each iteration step. As long as we choose fi uniformly from the data set, we find that this estimator is unbiased: E[w^t+1]=wttE[(fi)(wt)]=wtt(f)(wt)=wt+1 This is known as stochastic gradient descent. In order to ensure that we use all available data, we should choose the maximum number of iterations to be several times larger than the data set. There are also variations on this scheme where the data point used at each step is selected sequentially an array of data points. In that case, the update rule would be We can then estimate the update step by using the gradient for only one data point, w^t+1=wtt(fi)(wt) The data point to use should be chosen randomly at each iteration step. As long as we choose fi uniformly from the data set, we find that this estimator is unbiased: E[w^t+1]=wttE[(fi)(wt)]=wtt(f)(wt)=wt+1 This is known as stochastic gradient descent. In order to ensure that we use all available data, we should choose the maximum number of iterations to be several times larger than the data set. There are also variations on this scheme where the data point used at each step is selected sequentially an array of data points. In that case, the update rule would be w^t+1=wtt(ftmodN)(wt). A sequential stochastic gradient descent can be useful if selecting random data points on the fly is computationally expensive. This can occur for some storage mediums, such as hard drives, which have a slow random access time. By reading the data sequentially, we improve performance by ordering our read requests to the storage medium. In the sequential variation of stochastic gradient descent, how should we initialize this array of data points to minimize the number of iterations required to converge (i.e. increase the algorithmic performance of SGD itself)? In the order that the data points were observed experimentally. In random order. The initialization strategy for the array of data points does not matter. You have used 0 of 1 attempt Save