# Students should implement the following four functions in Solution_Q1.R: # generateData: takes as input the test results number, probability of positive results, and name of the test results file, and outputs the results file # loadData: takes as input the test results file and outputs the results as a dataframe # bayesianInference: takes as input the dataframe, prior, false positive rate, and hit rate, and outputs the vector of posterior probabilities # plotProsterior: takes as input the vector of posterior probabilities and name of the figure (where x axis is the number of data and y axis the corresponding posterior probabilities), and outputs the figure

source("Solution_Q1.R")

# Test results file testResultsFile = "testResults.csv" # Test results number testRusultsNum = 100 # Positive test results probability PosTestResultsProb = 0.9 # Posterior probabilitites figure posteriorsFig = "posteriorsFig"

# Probabilities prior = 0.001 # Prior probabilities fpr = 0.05 # False positive rate hr = 0.99 # Hit rate

# Takes as input the test results number, probability of positive results, and name of the test results file, and outputs the results file generateData

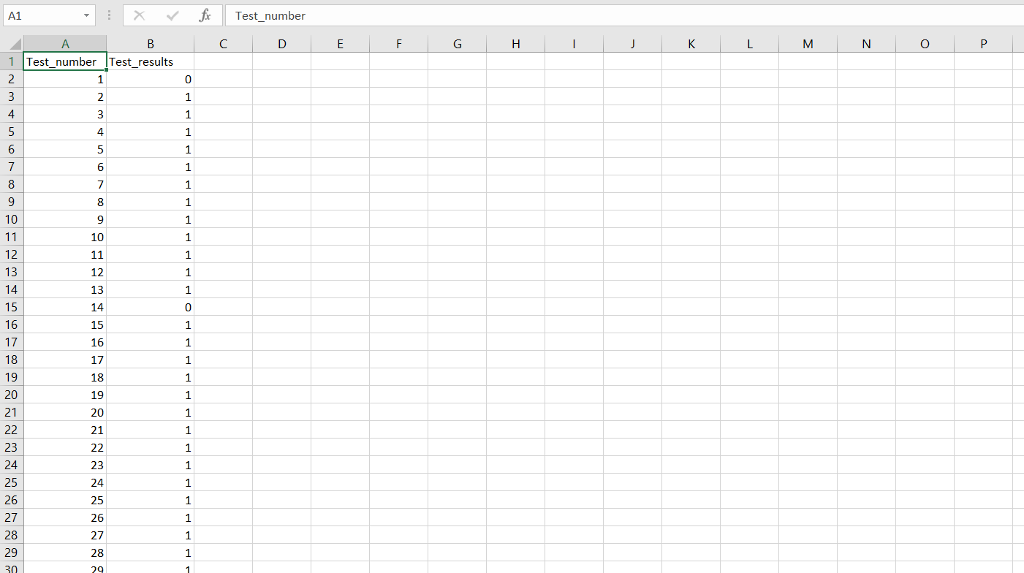
# Takes as input the test results file and outputs the results as a dataframe testResults = loadData(testResultsFile)

# Takes as input the dataframe, prior, false positive rate, and hit rate, and outputs the vector of posterior probabilities posteriors = bayesianInference(testResults, prior, fpr, hr)

# Takes as input the vector of posterior probabilities and name of the figure (where x axis is the number of data and y axis the corresponding posterior probabilities), and outputs the figure plotPosteriors(posteriors, posteriorsFig)

Input File:

Question 1: disease diagnosis (100 Points) Problem Follow up on the disease diagnosis example (page 9 of slides Bayes Rule.pdf) Suppose now we have multiple test results, where "1 " represents positive result and O negative The goal is to see how the posteriors change with the incremental data Deliverables Implement the following four functions in Solution Q1.R: generateData: takes as input the test results number, probability of positive results, and name of the test results file, and outputs the results file loadData: takes as input the test results file and outputs the results as a dataframe bayesianInference takes as input the dataframe, priorfalse positive rate, and hit rate, and outputs the vector of posterior probabilities plotPosteriors: takes as input the vector of posterior probabilities and name of the figure (where Y axis is the number of data and Y axis the corresponding posterior probabilities), and outputs the figure Hint: for function generateData, you may consider to use the sample function de- scribed in Exercise 1.2 (available on the blackboard) as in the Holmes' example, the posterior for test result Y, is the prior for result Yi+1 Question 1: disease diagnosis (100 Points) Problem Follow up on the disease diagnosis example (page 9 of slides Bayes Rule.pdf) Suppose now we have multiple test results, where "1 " represents positive result and O negative The goal is to see how the posteriors change with the incremental data Deliverables Implement the following four functions in Solution Q1.R: generateData: takes as input the test results number, probability of positive results, and name of the test results file, and outputs the results file loadData: takes as input the test results file and outputs the results as a dataframe bayesianInference takes as input the dataframe, priorfalse positive rate, and hit rate, and outputs the vector of posterior probabilities plotPosteriors: takes as input the vector of posterior probabilities and name of the figure (where Y axis is the number of data and Y axis the corresponding posterior probabilities), and outputs the figure Hint: for function generateData, you may consider to use the sample function de- scribed in Exercise 1.2 (available on the blackboard) as in the Holmes' example, the posterior for test result Y, is the prior for result Yi+1