Suppose that the distance, in miles, that people are willing to commute to work is an exponential random variable with mean 15 miles. (a) What percentage of people are willing to commute at most 14 miles to work? (b) 55% of people are willing to commute at most how many miles to work? (c) 18% of people are willing to commute at least how many miles to work?

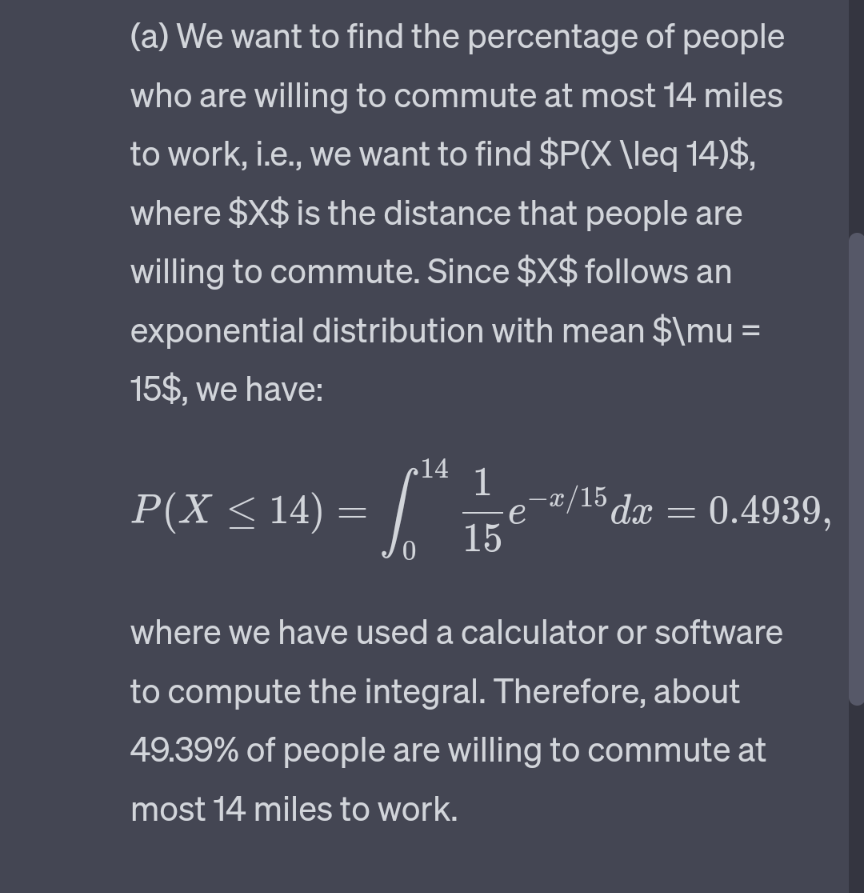
We are given that the distance that people are willing to commute to work follows an exponential distribution with mean 15 miles. Recall that the probability density function of an exponential distribution is given by: where $\\mu$ is the mean of the distribution. (a) We want to find the percentage of people who are willing to commute at most 14 miles to work, i.e., we want to find $P(X \\qu 14)$, where $X$ is the distance that people are willing to commute. Since $X$ follows an exponential distribution with mean $\\mu = 15$, we have: 14 1 / e_$/15d:r : 0.4939, 0 15 where we have used a calculator or software to compute the integral. Therefore, about 49.39% of people are willing to commute at most 14 miles to work. (b) We want to find the maximum distance $x$ such that 55% of people are willing to commute at most $x$ miles to work. In other words, we want to find $x$ such that $P(X \\leq x) = 055$. Since $X$ follows an exponential distribution with mean $\\mu = 15$, we have: m 1 / e_t/15dt= 1 _ ear/15- 0 15 Setting $P(X \\leq x) = 055$, we get: 0.55 : 1 efl\". Solving for $x$, we have: m : 15111(0.45) % 9.82. Therefore, 55% of people are willing to commute at most 9.82 miles to work. (c) We want to find the minimum distance $x$ such that 18% of people are willing to commute at least $x$ miles to work. In other words, we want to find $x$ such that $P(X \\geq X) = 018$. Since $X$ follows an exponential distribution with mean $\\mu = 15$, we have: Setting $P(X \\geq x) = 018$, we get: 0.18 = term/15. Solving for $x$, we have: a: = 15111(0.18) % 28.27. Therefore, 18% of people are willing to commute at least 28.27 miles to work