Suppose that the price at which q thousand flash drives can be sold is given by the demand equation

p = 12-0.4q dollars per drive, where 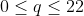. In addition, the cost of producing q thousand drives is given by the cost function: C(q)=26+0.85q thousand dollars.

1. Let R(q) denote the corresponding revenue function. Sketch a graph of both R(q) and C(q) on the same set of axes. Show only what is relevant.

2. Find the level of production (to the nearest flash drive) that maximizes revenue.

3. What is the selling price (per flash drive) that maximizes revenue?

4. What is the maximum possible revenue?

5. Find all break-even production levels, to the nearest flash drive.

6. Determine the level of sales that results in revenue of at least $85,000. Illustrate your results graphically.

Pleaseeee show all your work!