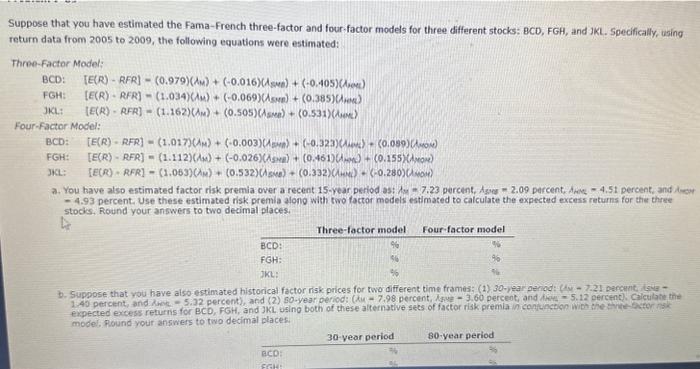
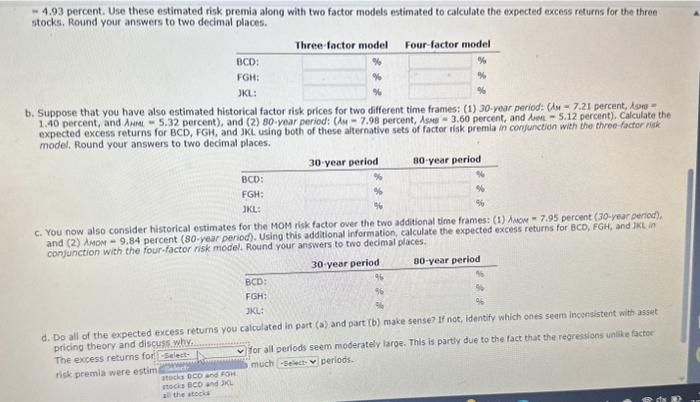
Suppose that you have estimated the Fama-French three-factor and four-factor models for three different stocks: BCD, FGH, and JKL. Specifically, using return data from 2005 to 2009 , the following equations were estimated: Three-Factor Model; BCD:[E(R)RFR]=(0.979)(M)+(0.016)(sue)+(0.405)(iped)FGH:[E(R)RFR]=(1.034)()+(0.069)(sme)+(0.385)(mea)JKa:[E(R)RFR]=(1.162)(AM)+(0.505)(ssen)+(0.531)(Ames) Four-Factor Model: -4.93 percent. Use these estimated risk premia alono with two factor models estimated to calculate the expected excess returns for the three stocis, Round your answers to two decimal places. model, Round your answers to two decimal places. - 4.93 percent. Use these estimated risk premia along with two factor models estimated to calculate the expected excess returns for the three stocks, Round your answers to two decimal places. b. Suppose that you have also estimated historical factor risk prices for two different time frames: (1) 30-year period: (ir =7.21 percent, lery = expected excess returns for BCD, FGH, and JKL using both of these alternative sets of facter risk premia in corjunction with the three-facter risk model, Round your answers to two decimal places. c. You now also consider historical estimates for the MOM risk factor over the two additional time frames: (1) A wom - 7.95 percent (30-year aenoc) and (2) AMON =9.84 percent ( 80 -year period). Using this additional information, Calculate the expected excess returns for 8CD, FGH, and JKL in conjunction with the four-factor nisk model. Round your arswers to two decimal places. d. Do all of the expected excess returns you calculated in part (a) and part (b) make sense? ir noc, pancur which ones seem incensistent with asset pricing theory and disfues whv. The excess retums for: risk premia were estim ateds 000 acd F0H ntodis BCD and 30 - all the stoda for all periods seem moderately large. This is partly due to the fact thut the regrestions unilie factor much periods. Suppose that you have estimated the Fama-French three-factor and four-factor models for three different stocks: BCD, FGH, and JKL. Specifically, using return data from 2005 to 2009 , the following equations were estimated: Three-Factor Model; BCD:[E(R)RFR]=(0.979)(M)+(0.016)(sue)+(0.405)(iped)FGH:[E(R)RFR]=(1.034)()+(0.069)(sme)+(0.385)(mea)JKa:[E(R)RFR]=(1.162)(AM)+(0.505)(ssen)+(0.531)(Ames) Four-Factor Model: -4.93 percent. Use these estimated risk premia alono with two factor models estimated to calculate the expected excess returns for the three stocis, Round your answers to two decimal places. model, Round your answers to two decimal places. - 4.93 percent. Use these estimated risk premia along with two factor models estimated to calculate the expected excess returns for the three stocks, Round your answers to two decimal places. b. Suppose that you have also estimated historical factor risk prices for two different time frames: (1) 30-year period: (ir =7.21 percent, lery = expected excess returns for BCD, FGH, and JKL using both of these alternative sets of facter risk premia in corjunction with the three-facter risk model, Round your answers to two decimal places. c. You now also consider historical estimates for the MOM risk factor over the two additional time frames: (1) A wom - 7.95 percent (30-year aenoc) and (2) AMON =9.84 percent ( 80 -year period). Using this additional information, Calculate the expected excess returns for 8CD, FGH, and JKL in conjunction with the four-factor nisk model. Round your arswers to two decimal places. d. Do all of the expected excess returns you calculated in part (a) and part (b) make sense? ir noc, pancur which ones seem incensistent with asset pricing theory and disfues whv. The excess retums for: risk premia were estim ateds 000 acd F0H ntodis BCD and 30 - all the stoda for all periods seem moderately large. This is partly due to the fact thut the regrestions unilie factor much periods