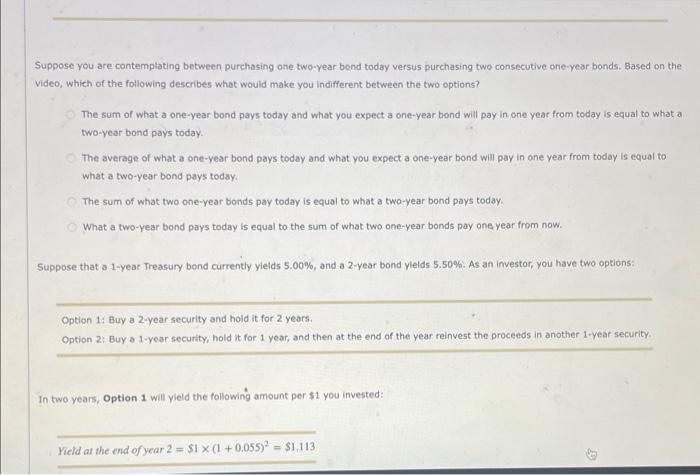
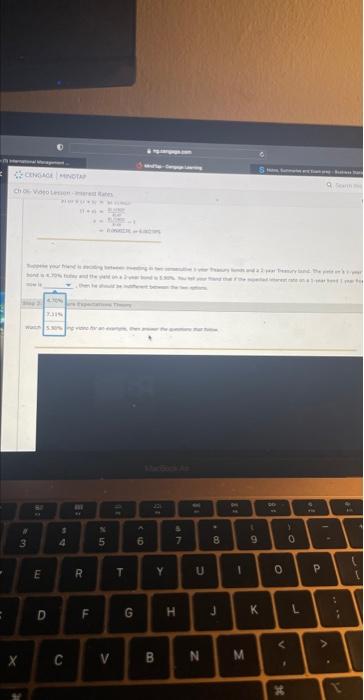
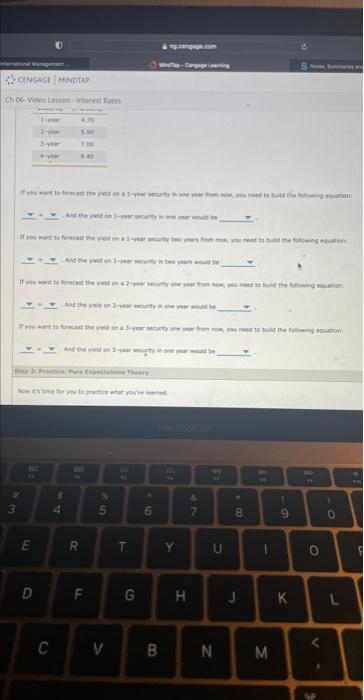
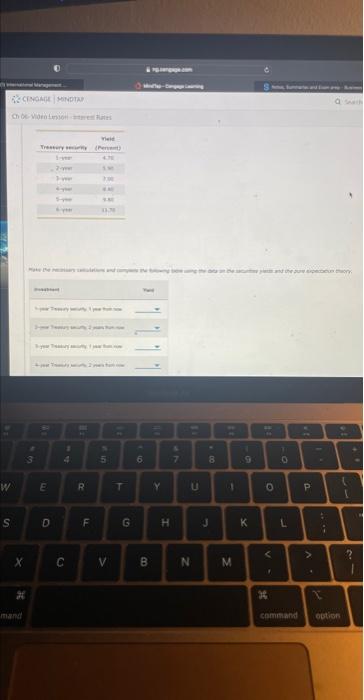
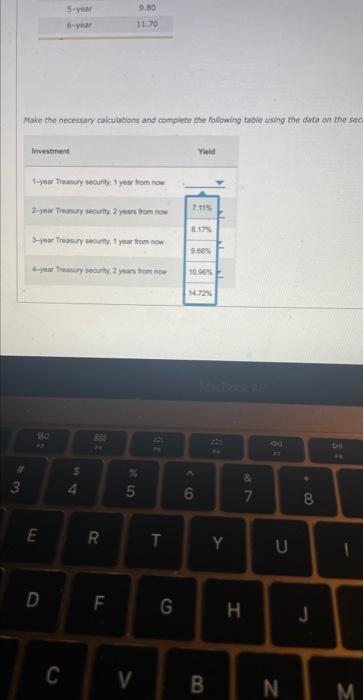
Suppose you are contemplating between purchasing one two-year bond today versus purchasing two consecutive one-year bonds. Based on the video, which of the following describes what would make you indifferent between the two options? The sum of what a one-year bond pays today and what you expect a one-year bond will pay in one year from today is equal to what a two-year bond pays today. The average of what a one-year bond pays today and what you expect a one-year bond will pay in one year from today is equal to what a two-year bond pays today. The sum of what two one-year bonds pay today is equal to what a twa-year bond pays today. What a two-year bond pays today is equal to the sum of what two one-year bonds pay one year from now. Suppose that a 1-year Treasury bond currently yields 5.00%, and a 2-year bond yields 5.50\%. As an investor, you have two options: Option 1: Buy a 2-year security and hold it for 2 years. Option 2: Buy a 1-year security, hold it for 1 year, and then at the end of the year reinvest the proceeds in another 1-year security. In two years, Option 1 will yield the following amount per $1 you invested: Yield at the end of year 2=$1(1+0.055)2=$1.113 In two years, uption 1 will yielo the rollowing amount per $1 you investeo: Yield at the end of year 2=$1(1+0.055)2=$1.113 The pure expectation theory implies that option 2 should yleld the same amount, which can be expressed as follows: Yield at the end of year 2=$1(1+0.05)(1+x)=$1.113, where x stands for the expected interest rate on a 1 -year Treasury secunty 1 year from now. $1(1+0.05)(1+x)51.05(1+x)(1+x)x=$1.113025=$1.113025=$101111005=50011110051=0.0600238,006.00238% Suppose your friend is deciding between investing in two consecutive 1-year Treasury bonds and a 2-year Treasury bond. The yield on a 1-year bond is 4.70% today and the yleld on a 2 -year bond is 5.90%. You tell your friend that if the expected interest rate on a 1 -year bond 1 year from now is , then he should be indifferent between the two options. Eh c6. Yided tesson interest trafer Th bevidentmon =tere fates Mohe the nccessary calculations and complate the following table using the dota an the sel Suppose you are contemplating between purchasing one two-year bond today versus purchasing two consecutive one-year bonds. Based on the video, which of the following describes what would make you indifferent between the two options? The sum of what a one-year bond pays today and what you expect a one-year bond will pay in one year from today is equal to what a two-year bond pays today. The average of what a one-year bond pays today and what you expect a one-year bond will pay in one year from today is equal to what a two-year bond pays today. The sum of what two one-year bonds pay today is equal to what a twa-year bond pays today. What a two-year bond pays today is equal to the sum of what two one-year bonds pay one year from now. Suppose that a 1-year Treasury bond currently yields 5.00%, and a 2-year bond yields 5.50\%. As an investor, you have two options: Option 1: Buy a 2-year security and hold it for 2 years. Option 2: Buy a 1-year security, hold it for 1 year, and then at the end of the year reinvest the proceeds in another 1-year security. In two years, Option 1 will yield the following amount per $1 you invested: Yield at the end of year 2=$1(1+0.055)2=$1.113 In two years, uption 1 will yielo the rollowing amount per $1 you investeo: Yield at the end of year 2=$1(1+0.055)2=$1.113 The pure expectation theory implies that option 2 should yleld the same amount, which can be expressed as follows: Yield at the end of year 2=$1(1+0.05)(1+x)=$1.113, where x stands for the expected interest rate on a 1 -year Treasury secunty 1 year from now. $1(1+0.05)(1+x)51.05(1+x)(1+x)x=$1.113025=$1.113025=$101111005=50011110051=0.0600238,006.00238% Suppose your friend is deciding between investing in two consecutive 1-year Treasury bonds and a 2-year Treasury bond. The yield on a 1-year bond is 4.70% today and the yleld on a 2 -year bond is 5.90%. You tell your friend that if the expected interest rate on a 1 -year bond 1 year from now is , then he should be indifferent between the two options. Eh c6. Yided tesson interest trafer Th bevidentmon =tere fates Mohe the nccessary calculations and complate the following table using the dota an the sel