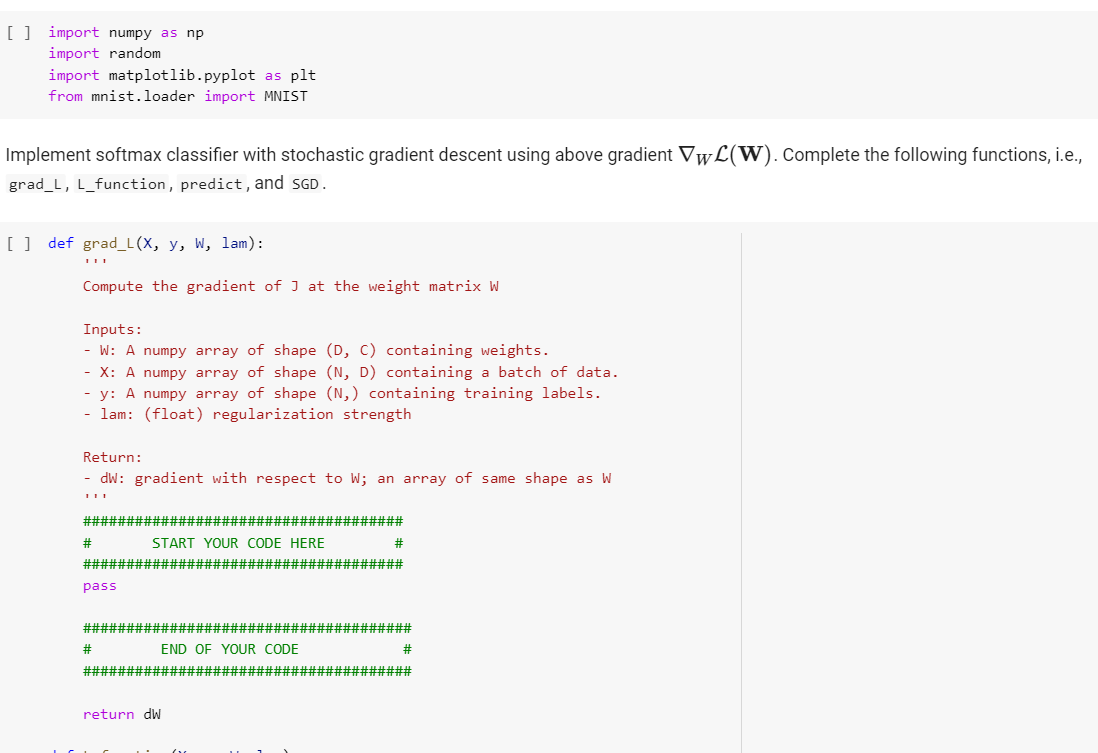
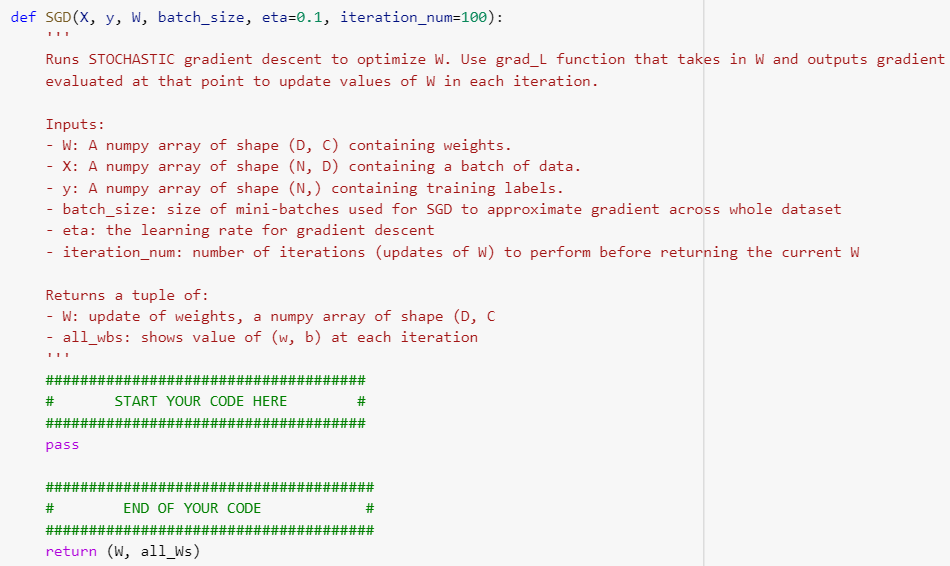
Task 2: Multinomial logistic regression (softmax classifier) on MNIST dataset In this task, we will implement the generalization of binary logistic regression to classify multiple classes (10 digits) on MNIST dataset. This classifier is known as multinomial logistic regression or softmax classifier. Concretely, suppose you have a dataset {(Xi, Yi)}N1 where X; RD (with D= 28 x 28 = 784), and label yi {0,...,9}. Consequently, we will assign a separate weight vector wc for each class 11, ..., lc (with C = 10, and l = 0,12 = 1,...,lc =9). Let W =(W1, ..., wc] RDXC. The probabilistic classification model is expressed as follows: exp(wxi) Pw(yi = 1c|W, xi) -1 exp(w) x;) For this problem, we will use cross-entropy loss with regularization. Accordingly, the negative log-likehood function is equal to 1 L(W) exp(w] xi) I(Yi =lc)log + . . N {j=1 exp(w|xi) where function I(Yi =le) = 1 if yi = lc is true, otherwise 0. Define the softmax(.) operator to be the function that takes in a vector 6 e RC and outputs a vector in RC whose ith component is equal to exp(ei) Clearly, this vector is nonnegative and sums to one. For each label Yi, let y; be the one-hot encoding of Yi (i.e., y; {0,1}) is - exp(@;) a vector of all zeros aside from a 1 in the yith index) It has been shown in the Question 5 of writing part that if {W) = softmax(WTx;), then VwL(W)=12*_xi(y; W)? + 1W. You can directly use this gradient to update weight matrix W when runing stochastic gradient descent. For simplicity, we do not consider the bias term in this task. = i=1 =1 [] import numpy as np import random import matplotlib.pyplot as plt from mnist.loader import MNIST Implement softmax classifier with stochastic gradient descent using above gradient VwL(W). Complete the following functions, i.e., grad_L, L_function, predict, and SGD. [] def grad_L(X, Y, W, lam): Compute the gradient of I at the weight matrix W Inputs: W: A numpy array of shape (D, C) containing weights. - X: A numpy array of shape (N, D) containing a batch of data. - y: A numpy array of shape (N,) containing training labels. - lam: (float) regularization strength Return: - dw: gradient with respect to W; an array of same shape as W ##################################### # START YOUR CODE HERE # ##################################### pass # END OF YOUR CODE # return dw def L_function(x, y, W, lam): Calculates the value of the loss function L(W) Inputs: - W: A numpy array of shape (D, C) containing weights. - X: A numpy array of shape (N, D) containing a batch of data. - y: A numpy array of shape (N,) containing training labels. - lam: (float) regularization strength Return: loss: single float # START YOUR CODE HERE pass # END OF YOUR CODE return loss def predict(X, W): Use the trained weights of this softmax classifier to predict labels for data points. Inputs: - X: A numpy array of shape (N, D) containing training data; there are N training samples each of dimension D. - W: A numpy array of shape (D, C) containing learned weights. Returns: - y_pred: Predicted labels for the data in X. y_pred is a 1-dimensional array of length N, and each element is an integer giving the predicted class. ######## START YOUR CODE HERE pass # # HE E# st # # HE Ett HE # # # END OF YOUR CODE EH return y_pred def SGD(x, y, W, batch_size, eta=0.1, iteration_num=100): Runs STOCHASTIC gradient descent to optimize W. Use grad_L function that takes in W and outputs gradient evaluated at that point to update values of W in each iteration. Inputs: - W: A numpy array of shape (D, C) containing weights. - X: A numpy array of shape (N, D) containing a batch of data. - y: A numpy array of shape (N,) containing training labels. - batch_size: size of mini-batches used for SGD to approximate gradient across whole dataset - eta: the learning rate for gradient descent iteration_num: number of iterations (updates of W) to perform before returning the current W Returns a tuple of: - W: update of weights, a numpy array of shape (D, C - all_wbs: shows value of (w, b) at each iteration START YOUR CODE HERE ### pass ### ##### # END OF YOUR CODE return (W, all_Ws) def reg_rate(x, y, W): Using data points X and trained weight W, make the predictions, and compares these against the true label stored in y to compute the recognition rate (i.e., accuracy) of softmax classifier Inputs: - W: A numpy array of shape (D, C) containing weights. X: A numpy array of shape (N, D) containing a batch of data. y: A numpy array of shape (N,) containing training labels. Returns: -accuracy y_pred = predict(X, W) accuracy = np.mean(y return accuracy == y_pred) Task 2: Multinomial logistic regression (softmax classifier) on MNIST dataset In this task, we will implement the generalization of binary logistic regression to classify multiple classes (10 digits) on MNIST dataset. This classifier is known as multinomial logistic regression or softmax classifier. Concretely, suppose you have a dataset {(Xi, Yi)}N1 where X; RD (with D= 28 x 28 = 784), and label yi {0,...,9}. Consequently, we will assign a separate weight vector wc for each class 11, ..., lc (with C = 10, and l = 0,12 = 1,...,lc =9). Let W =(W1, ..., wc] RDXC. The probabilistic classification model is expressed as follows: exp(wxi) Pw(yi = 1c|W, xi) -1 exp(w) x;) For this problem, we will use cross-entropy loss with regularization. Accordingly, the negative log-likehood function is equal to 1 L(W) exp(w] xi) I(Yi =lc)log + . . N {j=1 exp(w|xi) where function I(Yi =le) = 1 if yi = lc is true, otherwise 0. Define the softmax(.) operator to be the function that takes in a vector 6 e RC and outputs a vector in RC whose ith component is equal to exp(ei) Clearly, this vector is nonnegative and sums to one. For each label Yi, let y; be the one-hot encoding of Yi (i.e., y; {0,1}) is - exp(@;) a vector of all zeros aside from a 1 in the yith index) It has been shown in the Question 5 of writing part that if {W) = softmax(WTx;), then VwL(W)=12*_xi(y; W)? + 1W. You can directly use this gradient to update weight matrix W when runing stochastic gradient descent. For simplicity, we do not consider the bias term in this task. = i=1 =1 [] import numpy as np import random import matplotlib.pyplot as plt from mnist.loader import MNIST Implement softmax classifier with stochastic gradient descent using above gradient VwL(W). Complete the following functions, i.e., grad_L, L_function, predict, and SGD. [] def grad_L(X, Y, W, lam): Compute the gradient of I at the weight matrix W Inputs: W: A numpy array of shape (D, C) containing weights. - X: A numpy array of shape (N, D) containing a batch of data. - y: A numpy array of shape (N,) containing training labels. - lam: (float) regularization strength Return: - dw: gradient with respect to W; an array of same shape as W ##################################### # START YOUR CODE HERE # ##################################### pass # END OF YOUR CODE # return dw def L_function(x, y, W, lam): Calculates the value of the loss function L(W) Inputs: - W: A numpy array of shape (D, C) containing weights. - X: A numpy array of shape (N, D) containing a batch of data. - y: A numpy array of shape (N,) containing training labels. - lam: (float) regularization strength Return: loss: single float # START YOUR CODE HERE pass # END OF YOUR CODE return loss def predict(X, W): Use the trained weights of this softmax classifier to predict labels for data points. Inputs: - X: A numpy array of shape (N, D) containing training data; there are N training samples each of dimension D. - W: A numpy array of shape (D, C) containing learned weights. Returns: - y_pred: Predicted labels for the data in X. y_pred is a 1-dimensional array of length N, and each element is an integer giving the predicted class. ######## START YOUR CODE HERE pass # # HE E# st # # HE Ett HE # # # END OF YOUR CODE EH return y_pred def SGD(x, y, W, batch_size, eta=0.1, iteration_num=100): Runs STOCHASTIC gradient descent to optimize W. Use grad_L function that takes in W and outputs gradient evaluated at that point to update values of W in each iteration. Inputs: - W: A numpy array of shape (D, C) containing weights. - X: A numpy array of shape (N, D) containing a batch of data. - y: A numpy array of shape (N,) containing training labels. - batch_size: size of mini-batches used for SGD to approximate gradient across whole dataset - eta: the learning rate for gradient descent iteration_num: number of iterations (updates of W) to perform before returning the current W Returns a tuple of: - W: update of weights, a numpy array of shape (D, C - all_wbs: shows value of (w, b) at each iteration START YOUR CODE HERE ### pass ### ##### # END OF YOUR CODE return (W, all_Ws) def reg_rate(x, y, W): Using data points X and trained weight W, make the predictions, and compares these against the true label stored in y to compute the recognition rate (i.e., accuracy) of softmax classifier Inputs: - W: A numpy array of shape (D, C) containing weights. X: A numpy array of shape (N, D) containing a batch of data. y: A numpy array of shape (N,) containing training labels. Returns: -accuracy y_pred = predict(X, W) accuracy = np.mean(y return accuracy == y_pred)