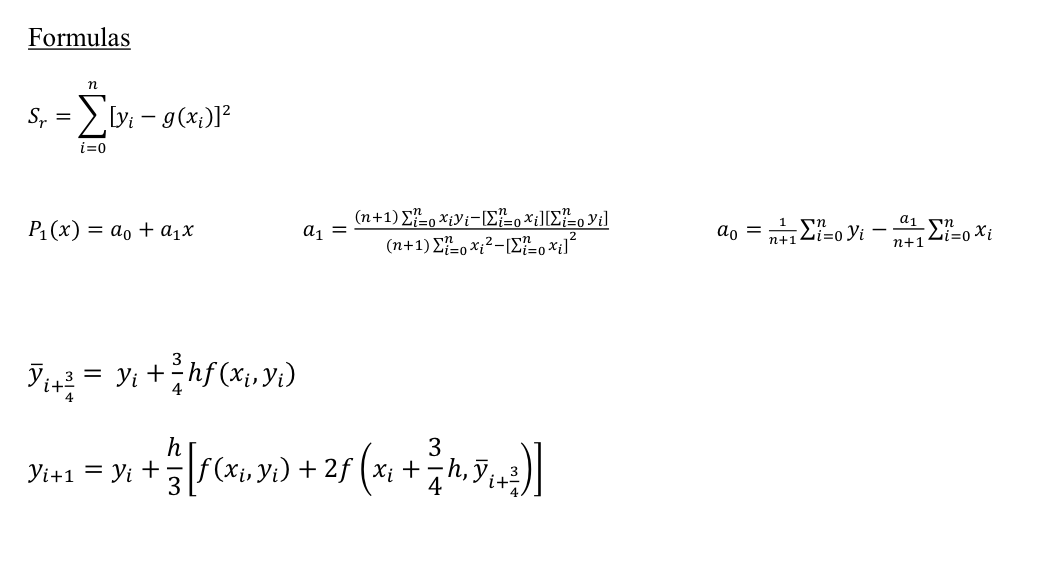
Taylo Formulas Vm+1 = Avm ||Avm|| B = A I B (A 2)(A-1) h h y(xo + h) = y(x0) + hy' (xo) + "(x) + 3y" (x0) + ... RR h Yi+1 = y +[k + 2k2+2k3 + k4] k = f (xi, yi) h 1 k = f (x + y +hk) h k3 = f(x1+ y+hk) k4= f(x+h, y + hk3) Forward 22 Buonund 22 Central 22 22 ax Ui+1,j - ui,j Ax Ui,j-ui-1,j Ax Ui+1,j - 2Ax - U-1,j ui-1,j 2ui,jui+1,j (Ax) Formulas n S = [y = g(x)] i=0 P(x) = a + ax a = V = y +hf(x, y) h (n+1) {=oXiVi=[?=o xt][?=oVi] (n+1) x2 -[=oxi] 3 Yi+1 = Yi + + } } [ f (x, y ) + 2 f ( x 2 + 3 / h, y + ) ] ao = - a1 n+1 3) The transient temperature distribution of a thin rod which is heated at one end may be obtained by solving the partial differential equation 0 < x < 1, t> 0 = at subject to the boundary conditions 1 (0, t) = -1, T(1,t) = 0 and initial condition T(x, 0) = 0. ax Using an explicit finite difference scheme with Ax = 0.2 and = temperature distribution at t = 0.1. = 0.5, determine the (Ax)2