Textbook Exercise 2 in Chapter 8. To prove NP, show an outline (pseudo-code okay) of the certifier algorithm and show that (a) its running time is polynomial and (b) the token (i.e., certificate) size is bounded by a polynomial function of the Diverse-Set problem instance size. To prove NP-hard, it would be easier to pick Independent-Set and reduce it to Diverse-Set. For this, provide the specific reduction mechanism and then show that (a) the reduction take polynomial time and (b) the Independent-Set problem instance has an independent set of size at most k if and only if the reduced Diverse-Set problem instance has a diverse set of size at most k.

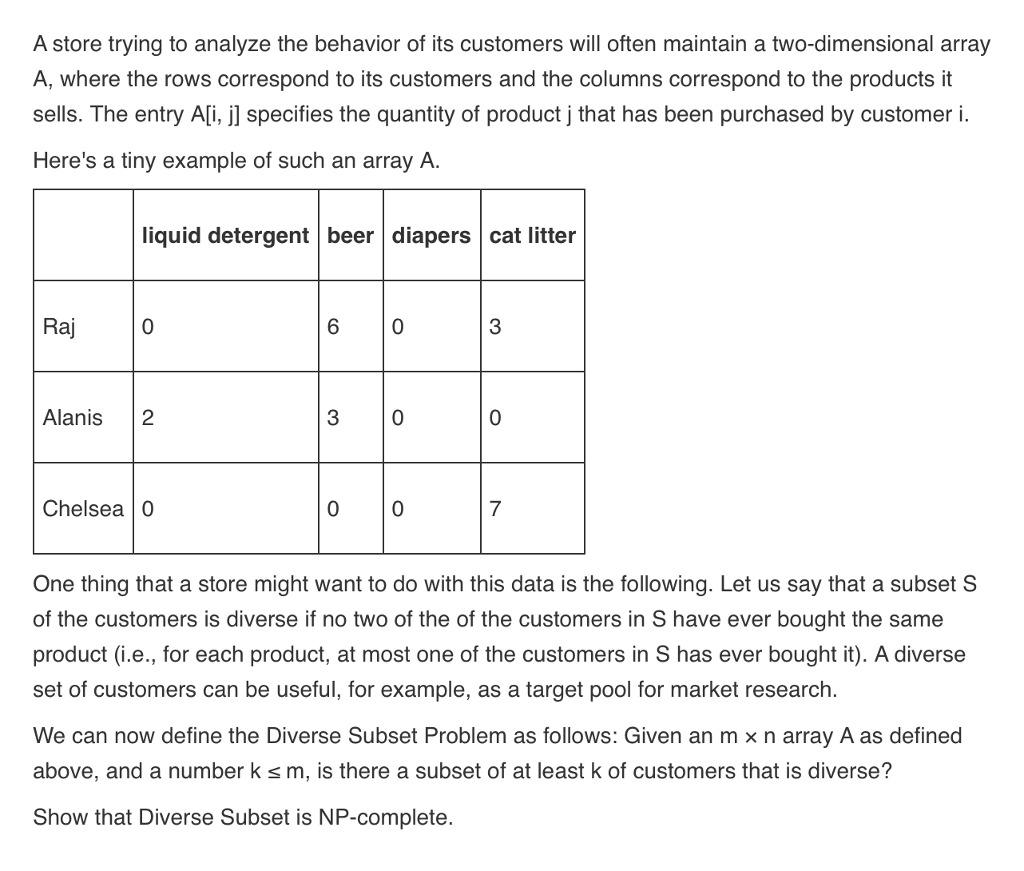
A store trying to analyze the behavior of its customers will often maintain a two-dimensional array A, where the rows correspond to its customers and the columns correspond to the products it sells. The entry Ali, jl specifies the quantity of product j that has been purchased by customer i. Here's a tiny example of such an array A. liquid detergent beer diapers cat litter 6 0 Alanis 0 Chelsea 0 One thing that a store might want to do with this data is the following. Let us say that a subset S of the customers is diverse if no two of the of the customers in S have ever bought the same product (i.e., for each product, at most one of the customers in S has ever bought it). A diverse set of customers can be useful, for example, as a target pool for market research. We can now define the Diverse Subset Problem as follows: Given an m x n array Aas defined above, and a number k s m, is there a subset of at least k of customers that is diverse? Show that Diverse Subset is NP-complete. A store trying to analyze the behavior of its customers will often maintain a two-dimensional array A, where the rows correspond to its customers and the columns correspond to the products it sells. The entry Ali, jl specifies the quantity of product j that has been purchased by customer i. Here's a tiny example of such an array A. liquid detergent beer diapers cat litter 6 0 Alanis 0 Chelsea 0 One thing that a store might want to do with this data is the following. Let us say that a subset S of the customers is diverse if no two of the of the customers in S have ever bought the same product (i.e., for each product, at most one of the customers in S has ever bought it). A diverse set of customers can be useful, for example, as a target pool for market research. We can now define the Diverse Subset Problem as follows: Given an m x n array Aas defined above, and a number k s m, is there a subset of at least k of customers that is diverse? Show that Diverse Subset is NP-complete