Answered step by step
Verified Expert Solution
Question
1 Approved Answer
th Submit quiz point(s) possible a. Use the Intermediate Value Theorem to show that the following equation has a solution on the given interval. b.
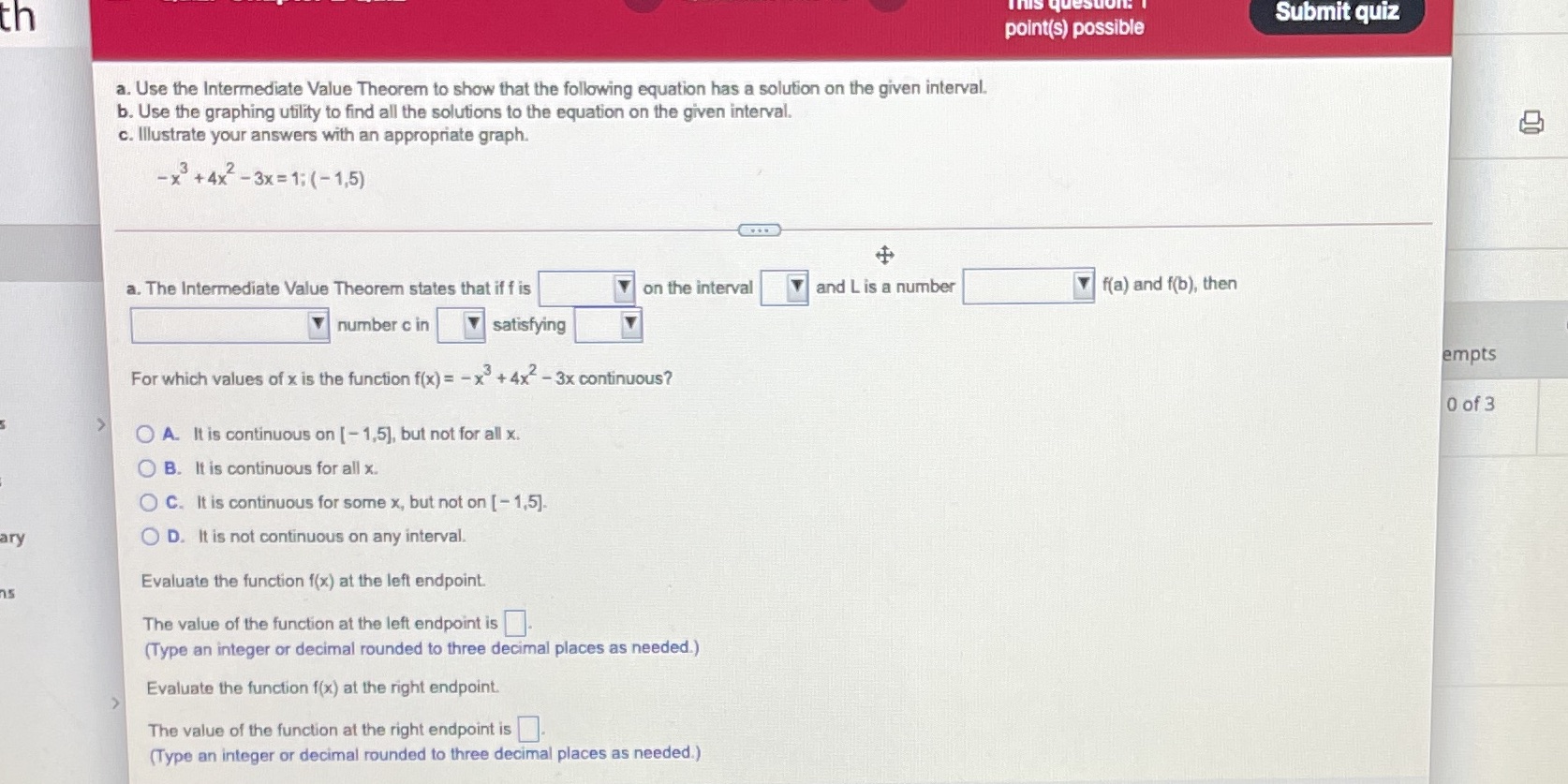
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


