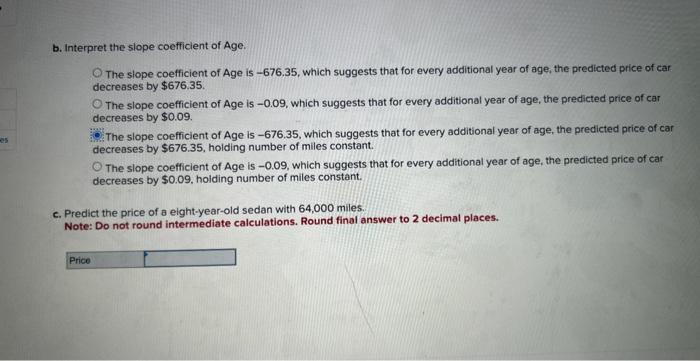
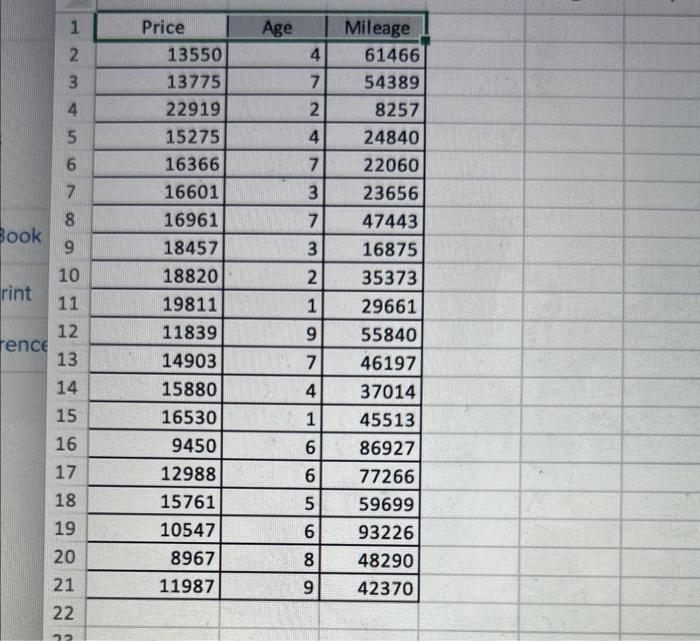
The accompanying data file shows the price, the age, and the mileage for 20 used sedans. Click here for the Excel Data File a. Estimate the sample regression equation that enables us to predict the price of a sedan on the basis of its age and mileage. Note: Negative values should be indicated by a minus sign. Round your answers to 2 decimal places. [If you are using R to obtain the output, then first enter the following command at the prompt: options(scipen-10). This will ensure that the output is not in scientific notation.] b. Interpret the slope coefficient of Age. The siope coefficient of Age is -676.35 , which suggests that for every additional year of age, the predicted price of car decreases by $676.35. The slope coefficient of Age is -0.09 , which suggests that for every additional year of age, the predicted price of car decreases by $0.09 The slope coefficient of Age is -676.35 , which suggests that for every additional year of age, the predicted price of car decreases by $676.35, holding number of miles constant. The slope coefficient of Age is -0.09 , which suggests that for every additional year of age, the predicted price of car decreases by $0.09, holding number of miles constant. b. Interpret the slope coefficlent of Age. The slope coefficient of Age is -676.35 , which suggests that for every additional year of age, the predicted price of car: decreases by $676.35. The slope coefficient of Age is -0.09 , which suggests that for every additional year of age, the predicted price of car decreases by $0.09 The slope coefficient of Age is -676.35 , which suggests that for every additional year of age, the predicted price of car decreases by $676.35, hoiding number of miles constant. The slope coefficient of Age is -0.09 , which suggests that for every additional year of age, the predicted price of car decreases by $0.09, holding number of miles constant. c. Predict the price of a eight-year-old sedan with 64,000 miles. Note: Do not round intermediate calculations. Round final answer to 2 decimal places. \begin{tabular}{|r|r|r|r|} \hline 1 & Price & \multicolumn{1}{|c|}{ Age } & Mileage \\ \cline { 2 - 4 } & 13550 & 4 & 61466 \\ \hline 3 & 13775 & 7 & 54389 \\ \hline 4 & 22919 & 2 & 8257 \\ \hline 5 & 15275 & 4 & 24840 \\ \hline 6 & 16366 & 7 & 22060 \\ \hline 7 & 16601 & 3 & 23656 \\ \hline 8 & 16961 & 7 & 47443 \\ \hline 9 & 18457 & 3 & 16875 \\ \hline 10 & 18820 & 2 & 35373 \\ \hline 11 & 19811 & 1 & 29661 \\ \hline 12 & 11839 & 9 & 55840 \\ \hline 13 & 14903 & 7 & 46197 \\ \hline 14 & 15880 & 4 & 37014 \\ \hline 15 & 16530 & 1 & 45513 \\ \hline 16 & 9450 & 6 & 86927 \\ \hline 17 & 12988 & 6 & 77266 \\ \hline 18 & 15761 & 5 & 59699 \\ \hline 19 & 10547 & 6 & 93226 \\ \hline 20 & 8967 & 8 & 48290 \\ \hline 21 & 11987 & 9 & 42370 \\ \hline \end{tabular} The accompanying data file shows the price, the age, and the mileage for 20 used sedans. Click here for the Excel Data File a. Estimate the sample regression equation that enables us to predict the price of a sedan on the basis of its age and mileage. Note: Negative values should be indicated by a minus sign. Round your answers to 2 decimal places. [If you are using R to obtain the output, then first enter the following command at the prompt: options(scipen-10). This will ensure that the output is not in scientific notation.] b. Interpret the slope coefficient of Age. The siope coefficient of Age is -676.35 , which suggests that for every additional year of age, the predicted price of car decreases by $676.35. The slope coefficient of Age is -0.09 , which suggests that for every additional year of age, the predicted price of car decreases by $0.09 The slope coefficient of Age is -676.35 , which suggests that for every additional year of age, the predicted price of car decreases by $676.35, holding number of miles constant. The slope coefficient of Age is -0.09 , which suggests that for every additional year of age, the predicted price of car decreases by $0.09, holding number of miles constant. b. Interpret the slope coefficlent of Age. The slope coefficient of Age is -676.35 , which suggests that for every additional year of age, the predicted price of car: decreases by $676.35. The slope coefficient of Age is -0.09 , which suggests that for every additional year of age, the predicted price of car decreases by $0.09 The slope coefficient of Age is -676.35 , which suggests that for every additional year of age, the predicted price of car decreases by $676.35, hoiding number of miles constant. The slope coefficient of Age is -0.09 , which suggests that for every additional year of age, the predicted price of car decreases by $0.09, holding number of miles constant. c. Predict the price of a eight-year-old sedan with 64,000 miles. Note: Do not round intermediate calculations. Round final answer to 2 decimal places. \begin{tabular}{|r|r|r|r|} \hline 1 & Price & \multicolumn{1}{|c|}{ Age } & Mileage \\ \cline { 2 - 4 } & 13550 & 4 & 61466 \\ \hline 3 & 13775 & 7 & 54389 \\ \hline 4 & 22919 & 2 & 8257 \\ \hline 5 & 15275 & 4 & 24840 \\ \hline 6 & 16366 & 7 & 22060 \\ \hline 7 & 16601 & 3 & 23656 \\ \hline 8 & 16961 & 7 & 47443 \\ \hline 9 & 18457 & 3 & 16875 \\ \hline 10 & 18820 & 2 & 35373 \\ \hline 11 & 19811 & 1 & 29661 \\ \hline 12 & 11839 & 9 & 55840 \\ \hline 13 & 14903 & 7 & 46197 \\ \hline 14 & 15880 & 4 & 37014 \\ \hline 15 & 16530 & 1 & 45513 \\ \hline 16 & 9450 & 6 & 86927 \\ \hline 17 & 12988 & 6 & 77266 \\ \hline 18 & 15761 & 5 & 59699 \\ \hline 19 & 10547 & 6 & 93226 \\ \hline 20 & 8967 & 8 & 48290 \\ \hline 21 & 11987 & 9 & 42370 \\ \hline \end{tabular}