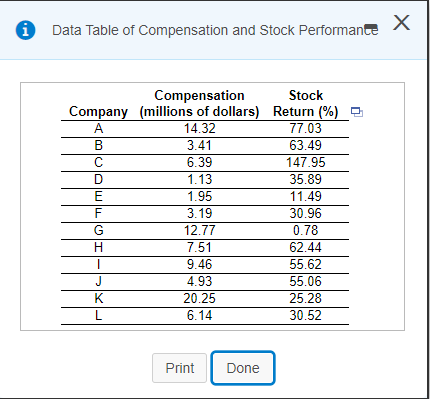
The accompanying data represent the total compensation for 12 randomly selected chief executive officers?(CEOs) and the?company's stock performance. Use the data to complete parts?(a) through?(d).

1 Data Table of Compensation and Stock Performance X Compensation Stock Company (millions of dollars) Return (%) A 14.32 77.03 B 3.41 63.49 6.39 147.95 D 1.13 35.89 1.95 11.49 3.19 30.96 12.77 0.78 H 7.51 62.44 - 9.46 55.62 4.93 55.06 K 20.25 25.28 6.14 30.52 Print Done(a) Treating compensation as the explanatory variable, x, use technology to determine the estimates of Po and By The estimate of By is (Round to three decimal places as needed.) The estimate of Bo is (Round to one decimal place as needed.)(b) Assuming that the residuals are normally distributed, test whether a linear relation exists between compensation and stock return at the = 0.10 level of significance. What are the null and alternative hypotheses? O A. Ho: Bo #0 H1 : Po = 0 OB. Ho: P, #0 H1 : 1. =0 O C. Ho: Po = 0 H1: PD #0 OD. Ho: By = 0 Hy : By #0 Compute the test statistic using technology. (Round to two decimal places as needed.) Compute the P-value using technology. (Round to three decimal places as needed.) State the appropriate conclusion. Choose the correct answer below. O A. Do not reject Ho. There is sufficient evidence to conclude that a linear relation exists between compensation and stock return. O B. Do not reject Ho. There is not sufficient evidence to conclude that a linear relation exists between compensation and stock retum. O C. Reject Ho. There is not sufficient evidence to conclude that a linear relation exists between compensation and stock return. O D. Reject Ho. There is sufficient evidence to conclude that a linear relation exists between compensation and stock return.(c) Assuming the residuals are normally distributed, construct a 90% confidence interval for the slope of the true least-squares regression line. Lower bound = Upper bound = (Round to two decimal places as needed.)(d) Based on your results to parts (b) and (c), would you recommend using the least-squares regression line to predict the stock return of a company based on the CEO's compensation? Why? What would be a good estimate of the stock return based on the data in the table? O A. Based on the results from parts (b) and (c), the regression line should not be used to predict the stock return. The mean stock return would be a good estimate of the stock return based on the data in the table. O B. Based on the results from parts (b), the regression line should not be used to predict the stock return. However, the results from part (c) indicate that the regression line should be used. The results are not conclusive and further analysis of the data is needed. O C. Based on the results from parts (b), the regression line could be used to predict the stock return. However, the results from part (b) indicate that the regression line should not be used. The results are not conclusive and further analysis of the data is needed. O D. The regression line could be used to predict the stock return. The test in part (b) and the confidence interval in part (c) both confirm that there is a relationship between the variables