The attached image is the work I've done for this problem. The question being asked is: What is the best decision strategy for the manager? What is the correct answer, and what are the steps to determine it?
A.Do not do the survey, select a large store
B.Do not do the survey, select a Small store
C.Do the survey. If the survey shows low demand then select a small store;If the survey shows high demand then select a large store.
D.Do the survey. If the survey shows low demand then select a large store; If the survey shows high demand then select a small store
E.None of the above is correc
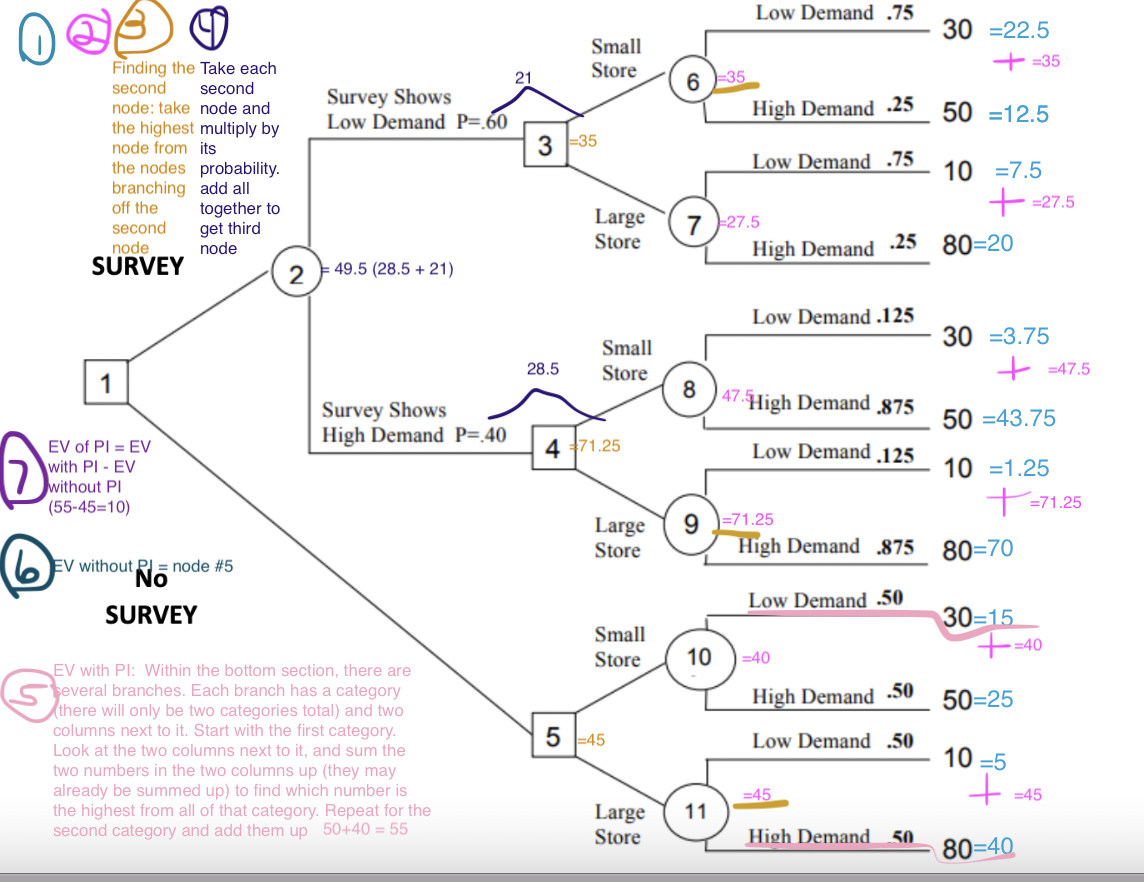
Low Demand .75 ooo Small Store 30 =22.5 +=35 21 Survey Shows Low Demand P=60 6 =35 High Demand .25 50 =12.5 3 =35 Finding the Take each second second node: take node and the highest multiply by node from its the nodes probability. branching add all off the together to second get third node node SURVEY 2 Low Demand .75 10 =7.5 +=27.5 7 27.5 High Demand .25 80=20 Large Store 49.5 (28.5 +21) Low Demand .125 30 -3.75 + =47.5 Small Store 28.5 1 8 | 47. High Demand 875 Survey Shows High Demand P= 40 50 -43.75 4 71.25 Low Demand.125 6) EV of PI = EV with PI - EV Jwithout PI (55-45=10) 10 = 1.25 t=71.25 9 )=71.25 Large Store High Demand .875 80=70 (6 v without Rla node #5 No Low Demand .50 SURVEY Small Store 30=15 +=40 10 -40 High Demand .50 50=25 5 -45 Low Demand .50 EV with Pl: Within the bottom section, there are several branches. Each branch has a category (there will only be two categories total) and two columns next to it. Start with the first category. Look at the two columns next to it, and sum the two numbers in the two columns up (they may already be summed up) to find which number is the highest from all of that category. Repeat for the second category and add them up 50+40 = 55 10 =5 + =45 =45 11 Large Store High Demand 50 80=40 Low Demand .75 ooo Small Store 30 =22.5 +=35 21 Survey Shows Low Demand P=60 6 =35 High Demand .25 50 =12.5 3 =35 Finding the Take each second second node: take node and the highest multiply by node from its the nodes probability. branching add all off the together to second get third node node SURVEY 2 Low Demand .75 10 =7.5 +=27.5 7 27.5 High Demand .25 80=20 Large Store 49.5 (28.5 +21) Low Demand .125 30 -3.75 + =47.5 Small Store 28.5 1 8 | 47. High Demand 875 Survey Shows High Demand P= 40 50 -43.75 4 71.25 Low Demand.125 6) EV of PI = EV with PI - EV Jwithout PI (55-45=10) 10 = 1.25 t=71.25 9 )=71.25 Large Store High Demand .875 80=70 (6 v without Rla node #5 No Low Demand .50 SURVEY Small Store 30=15 +=40 10 -40 High Demand .50 50=25 5 -45 Low Demand .50 EV with Pl: Within the bottom section, there are several branches. Each branch has a category (there will only be two categories total) and two columns next to it. Start with the first category. Look at the two columns next to it, and sum the two numbers in the two columns up (they may already be summed up) to find which number is the highest from all of that category. Repeat for the second category and add them up 50+40 = 55 10 =5 + =45 =45 11 Large Store High Demand 50 80=40







