The Birthday Problem

Problem Setup

The birthday problem is a famous problem with an interesting result. It is stated as follows:

"in a set of n people with randomly distributed birthdays, what is the probability that some pair of them will have the same birthday."

For example, P2=1/365 P366=1. (Think about why this should be the case.)

We will try to infer the behavior of Pn as a function of nn numerically, by generating many uniformly distributed samples of birthdays and checking whether any pair of birthdays is the same. For the purposes of this problem, assume there are 365 days in a year (ignore leap years).

In addition, your program must generate the following plot:

Plot of probability vs n. (Provide appropriate axes labels and a title.)

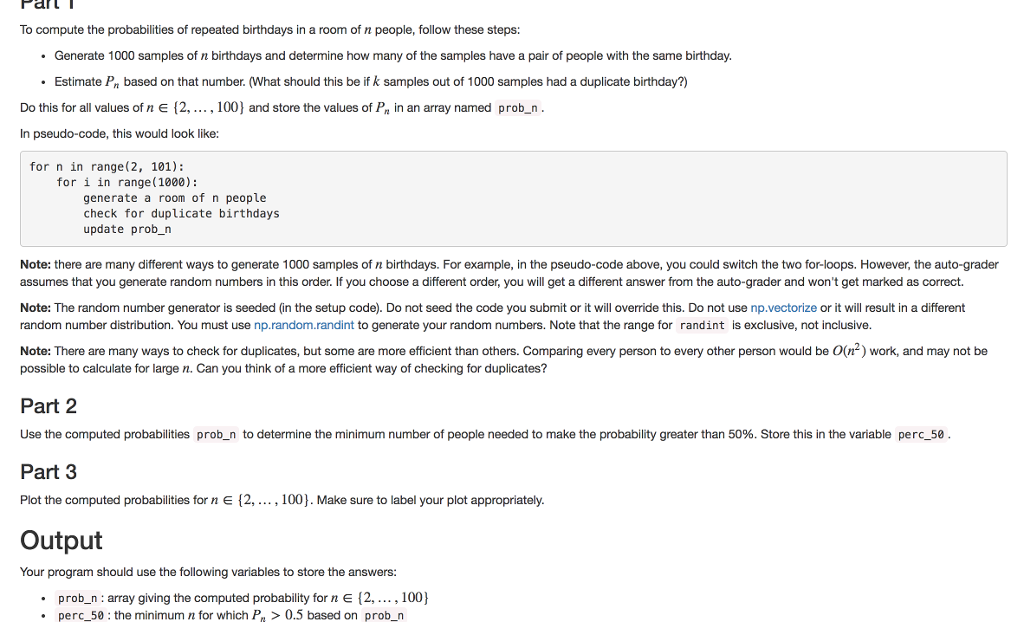
aft To compute the probabilities of repeated birthdays in a room of n people, follow these steps Generate 1000 samples of n birthdays and determine how many of the samples have a pair of people with the same birthday. . Estimate Pa based on that number, (what should this be if k samples out of 1000 samples had a duplicate birthday Do this for all values of n e [2,..., 100) and store the values of P in an array named prob_n. In pseudo-code, this would look like: for n in range (2, 101): for i in range (1000): generate a room of n people check for duplicate birthdays update prob_n Note: there are many different ways to generate 1000 samples of n birthdays. For example, in the pseudo-code above, you could switch the two for-loops. However, the auto-grader assumes that you generate random numbers in this order. If you choose a different order, you will get a different answer from the auto-grader and won't get marked as correct. Note: The random number generator is seeded (in the setup code). Do not seed the code you submit or it will override this. Do not use np.vectorize or it will result in a different random number distribution. You must use np.random.randint to generate your random numbers. Note that the range for randint is exclusive, not inclusive Note: There are many ways to check for duplicates, but some are more efficient than others. Comparing every person to every other person would be O(n2) work, and may not be possible to calculate for large n. Can you think of a more efficient way of checking for duplicates? Part 2 Use the computed probabilities prob n to determine the minimum number of people needed to make the probability greater than 50%. Store this in the variable peres Part 3 Plot the computed probabilities for n E [2,, 100]. Make sure to label your plot appropriately. Output Your program should use the following variables to store the answers: prob_n:array giving the computed probability for n E [2,.100 perc 50 the minimum n for which P >0.5 based on prob_n aft To compute the probabilities of repeated birthdays in a room of n people, follow these steps Generate 1000 samples of n birthdays and determine how many of the samples have a pair of people with the same birthday. . Estimate Pa based on that number, (what should this be if k samples out of 1000 samples had a duplicate birthday Do this for all values of n e [2,..., 100) and store the values of P in an array named prob_n. In pseudo-code, this would look like: for n in range (2, 101): for i in range (1000): generate a room of n people check for duplicate birthdays update prob_n Note: there are many different ways to generate 1000 samples of n birthdays. For example, in the pseudo-code above, you could switch the two for-loops. However, the auto-grader assumes that you generate random numbers in this order. If you choose a different order, you will get a different answer from the auto-grader and won't get marked as correct. Note: The random number generator is seeded (in the setup code). Do not seed the code you submit or it will override this. Do not use np.vectorize or it will result in a different random number distribution. You must use np.random.randint to generate your random numbers. Note that the range for randint is exclusive, not inclusive Note: There are many ways to check for duplicates, but some are more efficient than others. Comparing every person to every other person would be O(n2) work, and may not be possible to calculate for large n. Can you think of a more efficient way of checking for duplicates? Part 2 Use the computed probabilities prob n to determine the minimum number of people needed to make the probability greater than 50%. Store this in the variable peres Part 3 Plot the computed probabilities for n E [2,, 100]. Make sure to label your plot appropriately. Output Your program should use the following variables to store the answers: prob_n:array giving the computed probability for n E [2,.100 perc 50 the minimum n for which P >0.5 based on prob_n