Question: The Bolded words are the questions asked!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! Question 1) The Sea Wharf Restaurant would like to determine the best way to allocate a monthly advertising
The Bolded words are the questions asked!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Question 1) The Sea Wharf Restaurant would like to determine the best way to allocate a monthly advertising budget of $7,000.00between newspaper advertising and radio advertising. Management decided that at least 25% of the budget must be spent on each type of media and that the amount of money spent on local newspaper advertising must be at least twice the amount spent on radio advertising. A marketing consultant developed an index that measures audience exposure per dollar of advertising on a scale from 0 to 100, with higher values implying greater audience exposure. If the value of the index for local newspaper advertising is80and the value of the index for spot radio advertising is90,how should the restaurant allocate its advertising budget to maximize the value of total audience exposure?
(a)
Formulate a linear programming model that can be used to determine how the restaurant should allocate its advertising budget in order to maximize the value of total audience exposure. (AssumeNis the amount spent on newspaper advertising andRis the amount spent on radio advertising.)
Max
s.t.budget
minimum newspaper spending
minimum radio spending
comparison radio and newspaper spending
N,R?0
(b)
Develop a spreadsheet model and solve the problem using Excel Solver. (Round the Newspaper Dollars Allocated and the Radio Dollars Allocated to the nearest cent. Round the Total Exposure Index to the nearest integer.)
Newspaper Dollars Allocated$
Radio Dollars Allocated$
Total Exposure Index
Question 2) Blair & Rosen, Inc. (B&R), is a brokerage firm that specializes in investment portfolios designed to meet the specific risk tolerances of its clients. A client who contacted B&R this past week has a maximum of $75,000to invest. B&R's investment advisor decides to recommend a portfolio consisting of two investment funds: an Internet fund and a Blue Chip fund. The Internet fund has a projected annual return of8%, whereas the Blue Chip fund has a projected annual return of6%. The investment advisor requires that at most $50,000of the client's funds should be invested in the Internet fund. B&R services include a risk rating for each investment alternative. The Internet fund, which is the more risky of the two investment alternatives, has a risk rating of 6 per thousand dollars invested. The Blue Chip fund has a risk rating of 4 per thousand dollars invested. For example, if $10,000 is invested in each of the two investment funds, B&R's risk rating for the portfolio would be6(10) + 4(10) = 100.
Finally, B&R developed a questionnaire to measure each client's risk tolerance. Based on the responses, each client is classified as a conservative, moderate, or aggressive investor. Suppose that the questionnaire results classified the current client as a moderate investor. B&R recommends that a client who is a moderate investor limit his or her portfolio to a maximum risk rating of360.
(a)
Formulate a linear programming model to find the best investment strategy for this client. (AssumeNis the amount invested in the internet fund project andBis the amount invested in the Blue Chip fund. Express the amounts invested in thousands of dollars.)
Max
s.t.Available investment funds
Maximum investment in the internet fund
Maximum risk for a moderate investor
N,B?0
(b)
Build a spreadsheet model and solve the problem using Excel Solver. What is the recommended investment portfolio (in dollars) for this client?
internet fund$
blue chip fund$
What is the annual return (in dollars) for the portfolio?
$
(b)
Suppose that a second client with $75,000to invest has been classified as an aggressive investor. B&R recommends that the maximum portfolio risk rating for an aggressive investor is400. What is the recommended investment portfolio (in dollars) for this aggressive investor?
internet fund $
blue chip fund $
(d)
Suppose that a third client with $75,000to invest has been classified as a conservative investor. B&R recommends that the maximum portfolio risk rating for a conservative investor is240. Develop the recommended investment portfolio (in dollars) for the conservative investor.
internet fund$
blue chip fund$
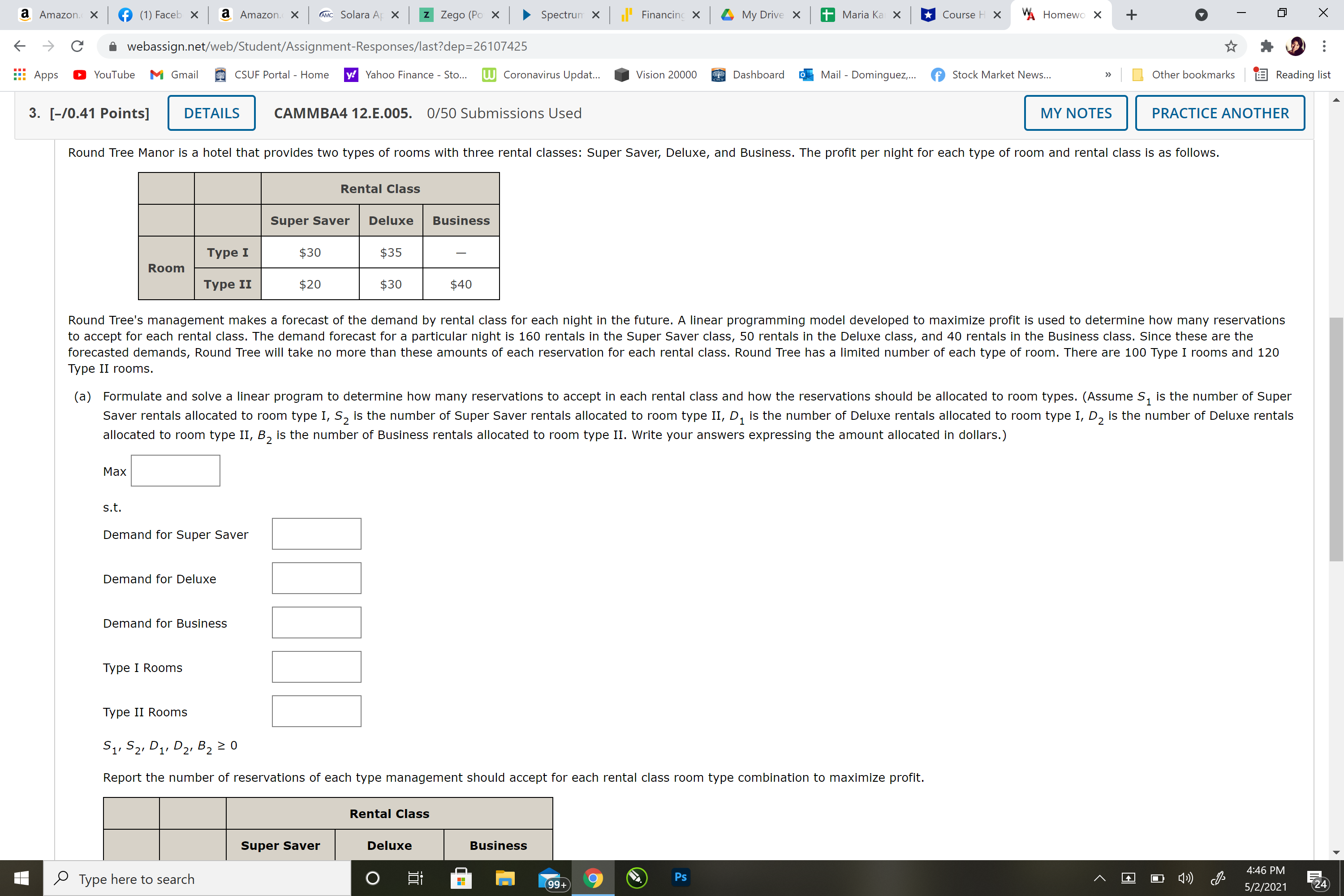
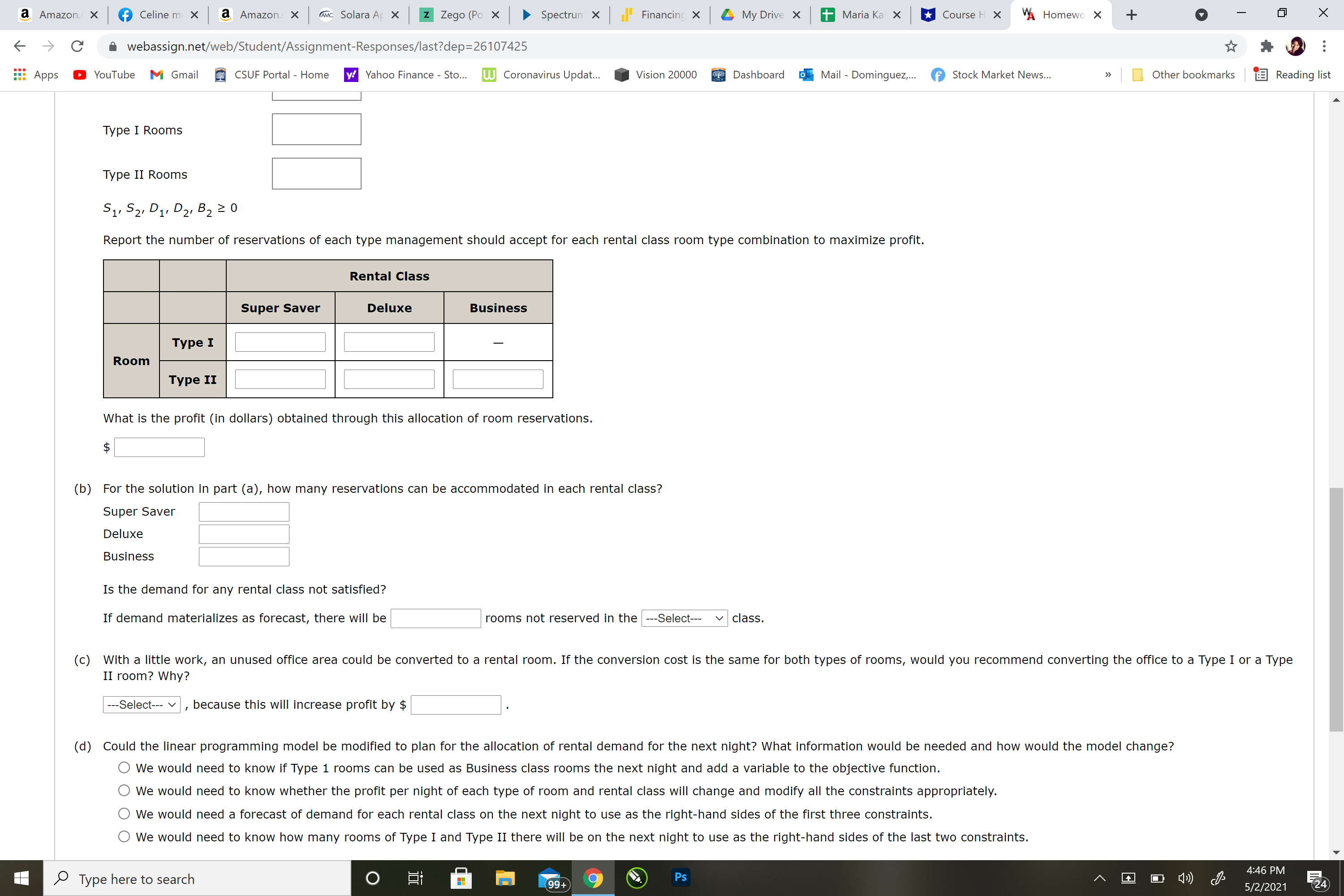
Question 3) Round Tree Manor is a hotel that provides two types of rooms with three rental classes: Super Saver, Deluxe, and Business. The profit per night for each type of room and rental class is as follows.
Rental ClassSuper SaverDeluxeBusinessRoomType I$30$35?Type II$20$30$40
Round Tree's management makes a forecast of the demand by rental class for each night in the future. A linear programming model developed to maximize profit is used to determine how many reservations to accept for each rental class. The demand forecast for a particular night is160rentalsin the Super Saver class,50rentalsin the Deluxe class, and40rentalsin the Business class. Since these are the forecasted demands, Round Tree will take no more than these amounts of each reservation for each rental class. Round Tree has a limited number of each type of room. There are 100 Type I rooms and 120 Type II rooms.
(a)
Formulate and solve a linear program to determine how many reservations to accept in each rental class and how the reservations should be allocated to room types. (AssumeS1is the number of Super Saver rentals allocated to room type I,S2is the number of Super Saver rentals allocated to room type II,D1is the number of Deluxe rentals allocated to room type I,D2is the number of Deluxe rentals allocated to room type II,B2is the number of Business rentals allocated to room type II. Write your answers expressing the amount allocated in dollars.)
Max
s.t.
Demand for Super Saver
Demand for Deluxe
Demand for Business
Type I Rooms
Type II RoomsS1,S2,D1,D2,B2?0
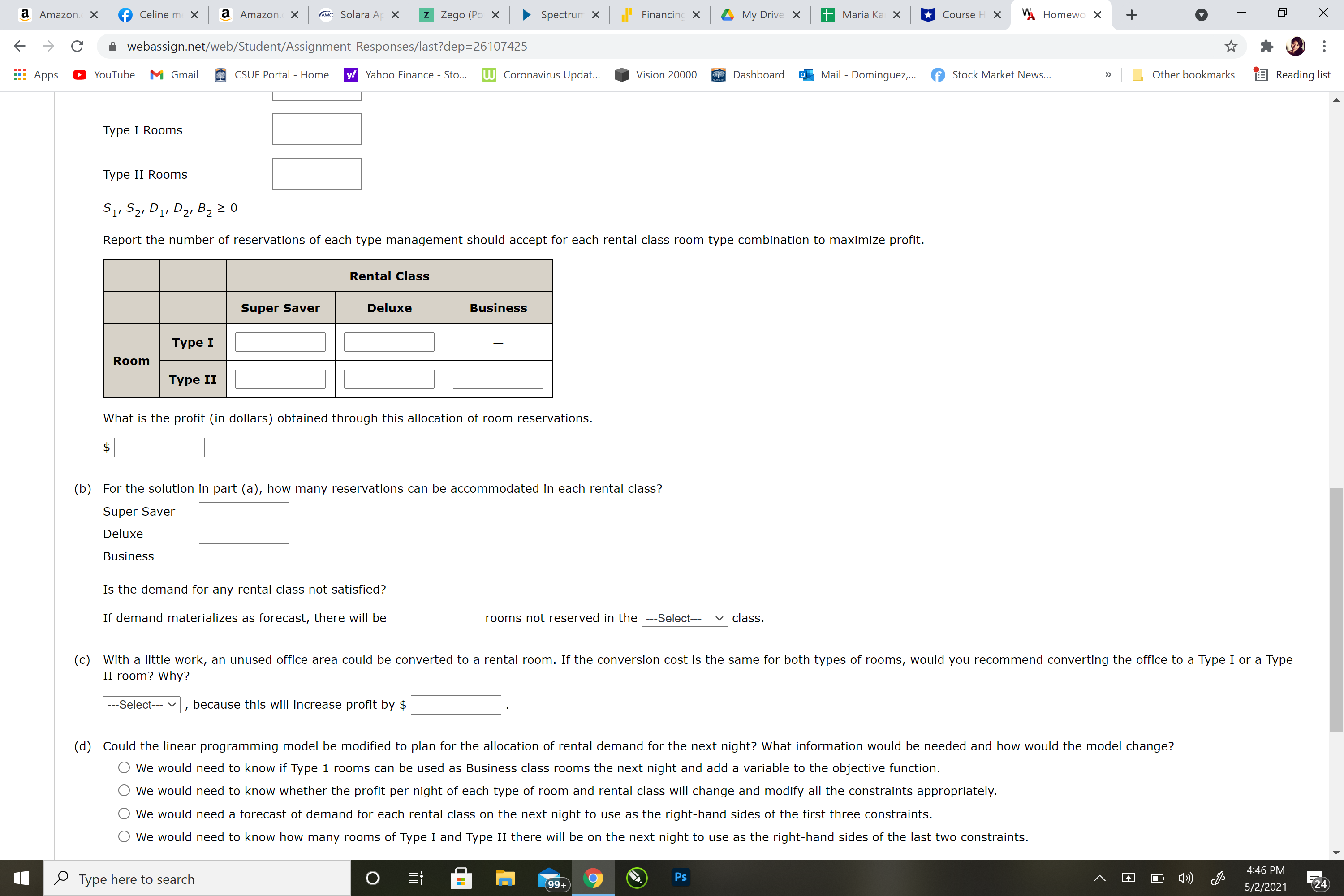
Report the number of reservations of each type management should accept for each rental class room type combination to maximize profit.
Rental ClassSuper SaverDeluxeBusinessRoomType I?Type II
What is the profit (in dollars) obtained through this allocation of room reservations.
$
(b)
For the solution in part (a), how many reservations can be accommodated in each rental class?
Super Saver
Deluxe
Bussiness
Is the demand for any rental class not satisfied?
If demand materializes as forecast, there will berooms not reserved in the
---Select---
(c)
With a little work, an unused office area could be converted to a rental room. If the conversion cost is the same for both types of rooms, would you recommend converting the office to a Type I or a Type II room? Why?
---Select---
Type I
Type II
,because this will increase profit by$.
(d)
Could the linear programming model be modified to plan for the allocation of rental demand for the next night? What information would be needed and how would the model change?
We would need to know if Type 1 rooms can be used as Business class rooms the next night and add a variable to the objective function.
We would need to know whether the profit per night of each type of room and rental class will change and modify all the constraints appropriately.
We would need a forecast of demand for each rental class on the next night to use as the right-hand sides of the first three constraints.
We would need to know how many rooms of Type I and Type II there will be on the next night to use as the right-hand sides of the last two constraints.
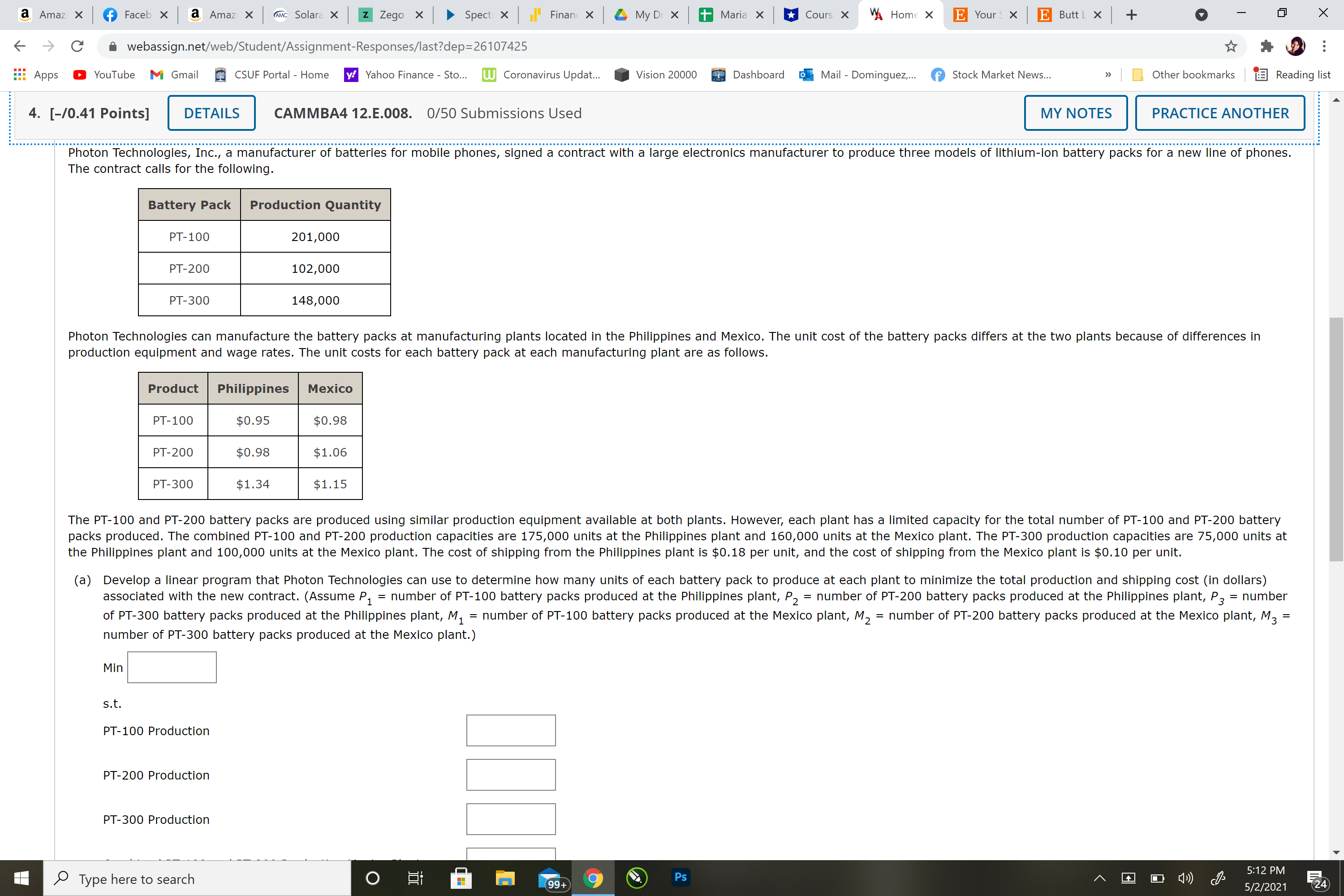
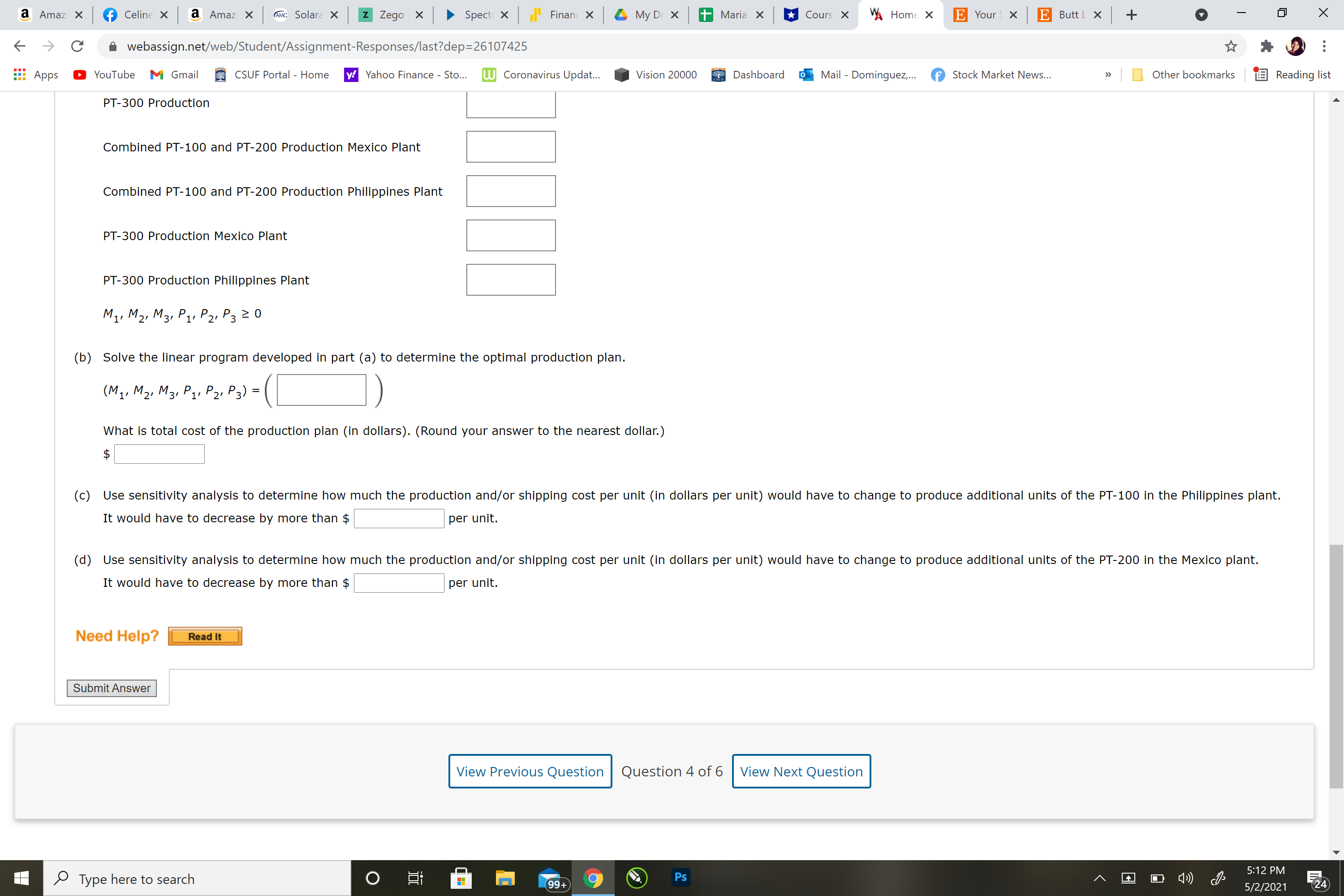
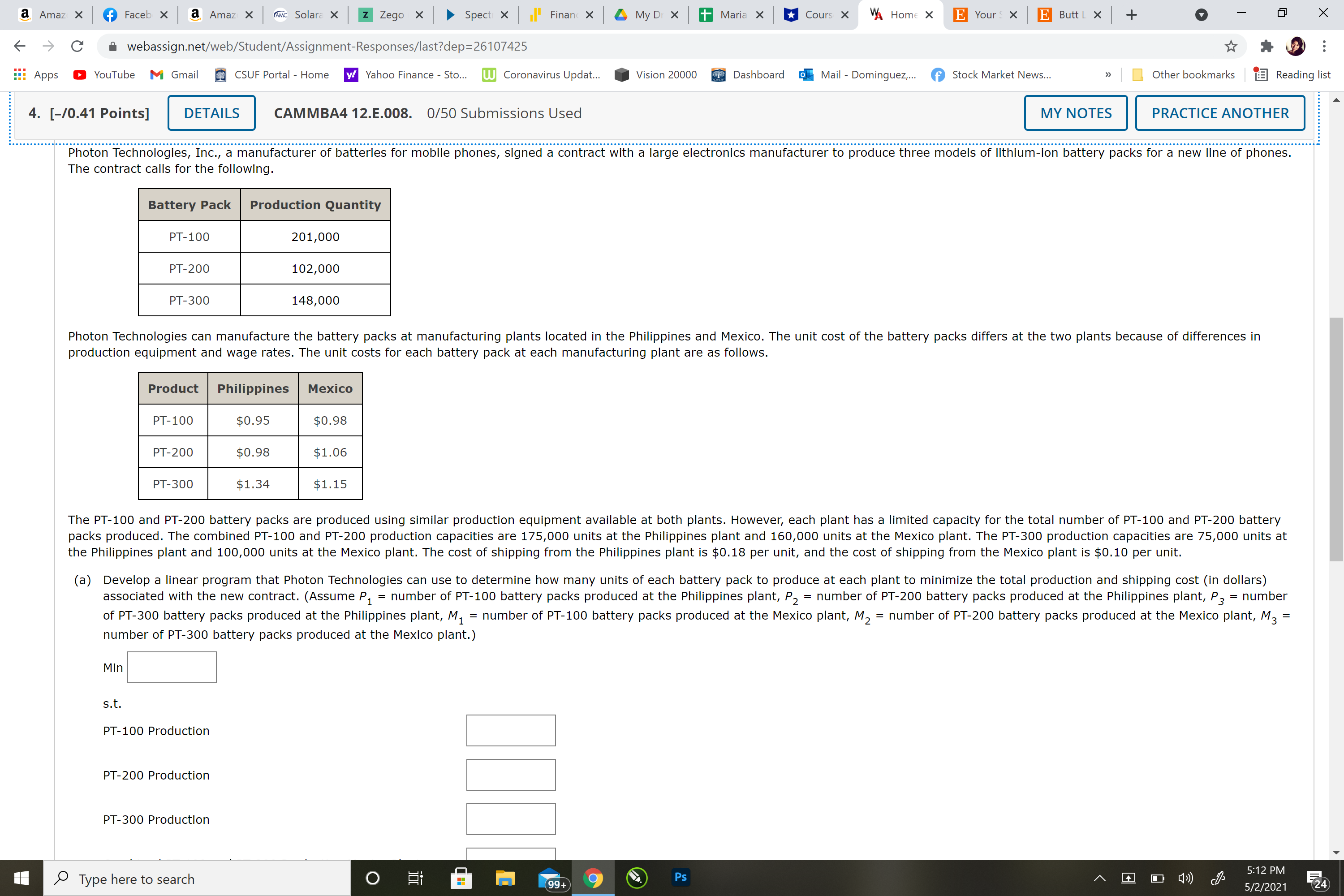
Question 4) Photon Technologies, Inc., a manufacturer of batteries for mobile phones, signed a contract with a large electronics manufacturer to produce three models of lithium-ion battery packs for a new line of phones. The contract calls for the following.
Battery PackProduction QuantityPT-100201,000PT-200102,000PT-300148,000
Photon Technologies can manufacture the battery packs at manufacturing plants located in the Philippines and Mexico. The unit cost of the battery packs differs at the two plants because of differences in production equipment and wage rates. The unit costs for each battery pack at each manufacturing plant are as follows.
ProductPhilippinesMexicoPT-100$0.95$0.98PT-200$0.98$1.06PT-300$1.34$1.15
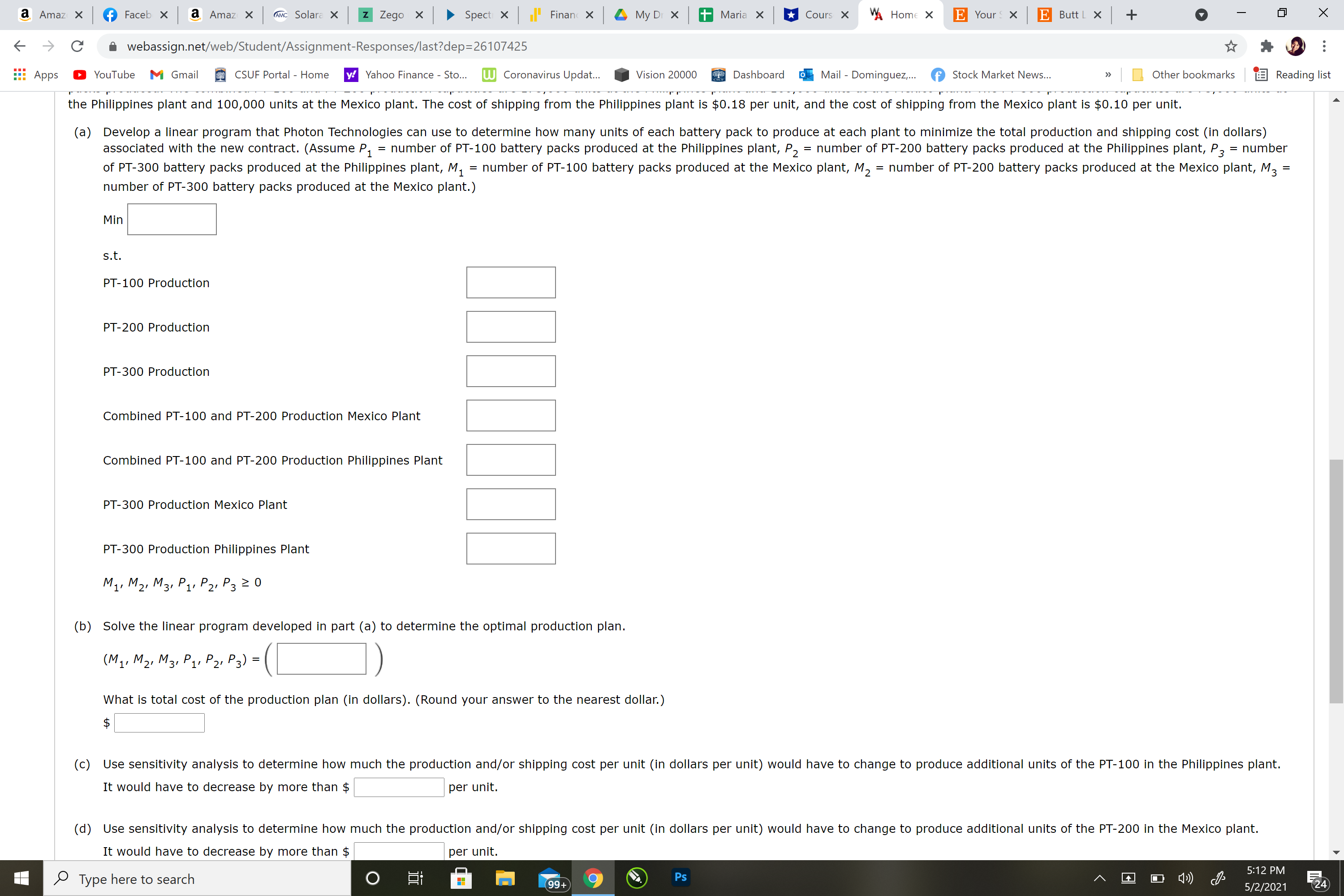
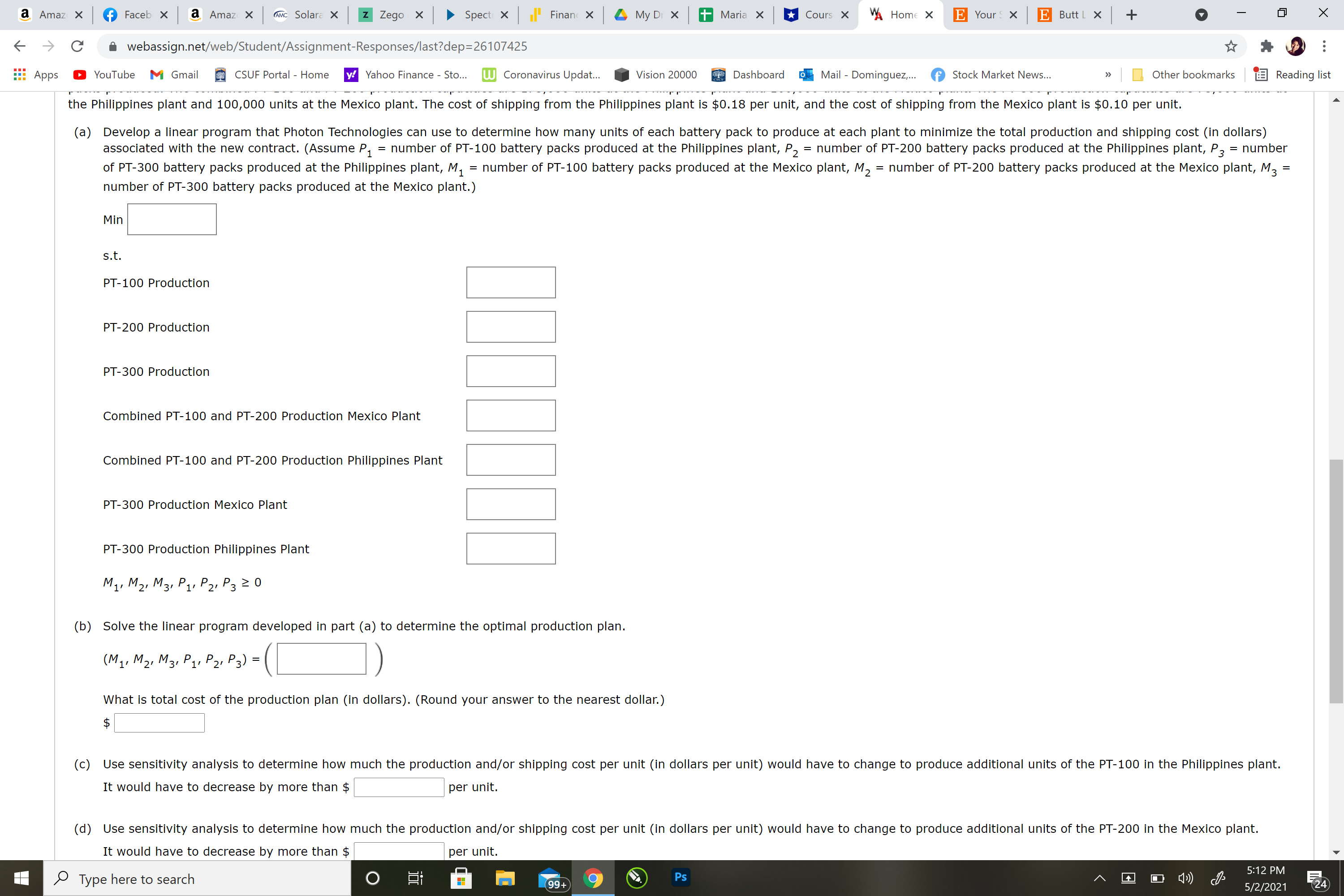
The PT-100 and PT-200 battery packs are produced using similar production equipment available at both plants. However, each plant has a limited capacity for the total number of PT-100 and PT-200 battery packs produced. The combined PT-100 and PT-200 production capacities are175,000 unitsat the Philippines plant and160,000 unitsat the Mexico plant. The PT-300 production capacities are75,000 unitsat the Philippines plant and100,000 unitsat the Mexico plant. The cost of shipping from the Philippines plant is $0.18 per unit, and the cost of shipping from the Mexico plant is $0.10 per unit.
(a)
Develop a linear program that Photon Technologies can use to determine how many units of each battery pack to produce at each plant to minimize the total production and shipping cost (in dollars) associated with the new contract. (AssumeP1=number of PT-100 battery packs produced at the Philippines plant,P2=number of PT-200 battery packs produced at the Philippines plant,P3=number of PT-300 battery packs produced at the Philippines plant,M1=number of PT-100 battery packs produced at the Mexico plant,M2=number of PT-200 battery packs produced at the Mexico plant,M3=number of PT-300 battery packs produced at the Mexico plant.)
Min
s.t.
PT-100 Production
PT-200 Production
PT-300 Production
Combined PT-100 and PT-200 Production Mexico Plant
Combined PT-100 and PT-200 Production Philippines Plant
PT-300 Production Mexico Plant
PT-300 Production Philippines Plant
M1,M2,M3,P1,P2,P3?0
(b)
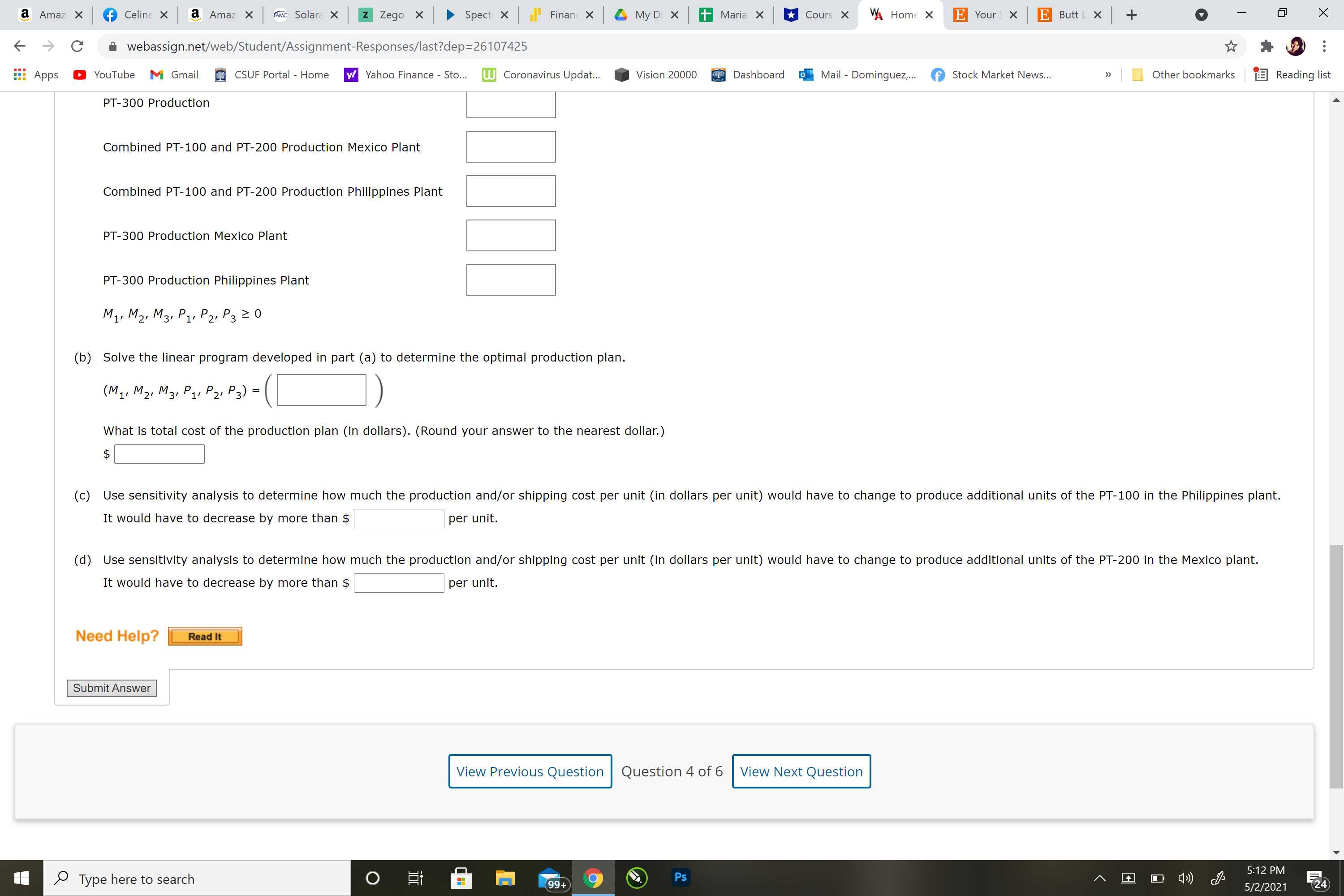
Solve the linear program developed in part (a) to determine the optimal production plan.
(M1,M2,M3,P1,P2,P3) =
What is total cost of the production plan (in dollars). (Round your answer to the nearest dollar.)
$
(c)
Use sensitivity analysis to determine how much the production and/or shipping cost per unit (in dollars per unit) would have to change to produce additional units of the PT-100 in the Philippines plant.
It would have to decrease by more than $per unit.
(d)
Use sensitivity analysis to determine how much the production and/or shipping cost per unit (in dollars per unit) would have to change to produce additional units of the PT-200 in the Mexico plant.
It would have to decrease by more than $per unit.
Question 5) The employee credit union at State University is planning the allocation of funds for the coming year. The credit union makes four types of loans to its members. In addition, the credit union invests in risk-free securities to stabilize income. The various revenue-producing investments, together with annual rates of return, are as follows.
Type of Loan/InvestmentAnnual Rate of Return (%)Automobile loans9Furniture loans11Other secured loans12Signature loans13Risk-free securities10
The credit union will have $2,400,000available for investment during the coming year. State laws and credit union policies impose the following restrictions on the composition of the loans and investments.
- Risk-free securities may not exceed 30% of the total funds available for investment.
- Signature loans may not exceed 10% of the funds invested in all loans (automobile, furniture, other secured, and signature loans).
- Furniture loans plus other secured loans may not exceed the automobile loans.
- Other secured loans plus signature loans may not exceed the funds invested in risk-free securities.
How should the $2,400,000be allocated to each of the loan/investment alternatives (in dollars) to maximize total annual return?
Automobile loans$
Furniture loans$
Other secured loans$
Signature loans$
Risk-free securities$
What is the projected total annual return (in dollars)? $
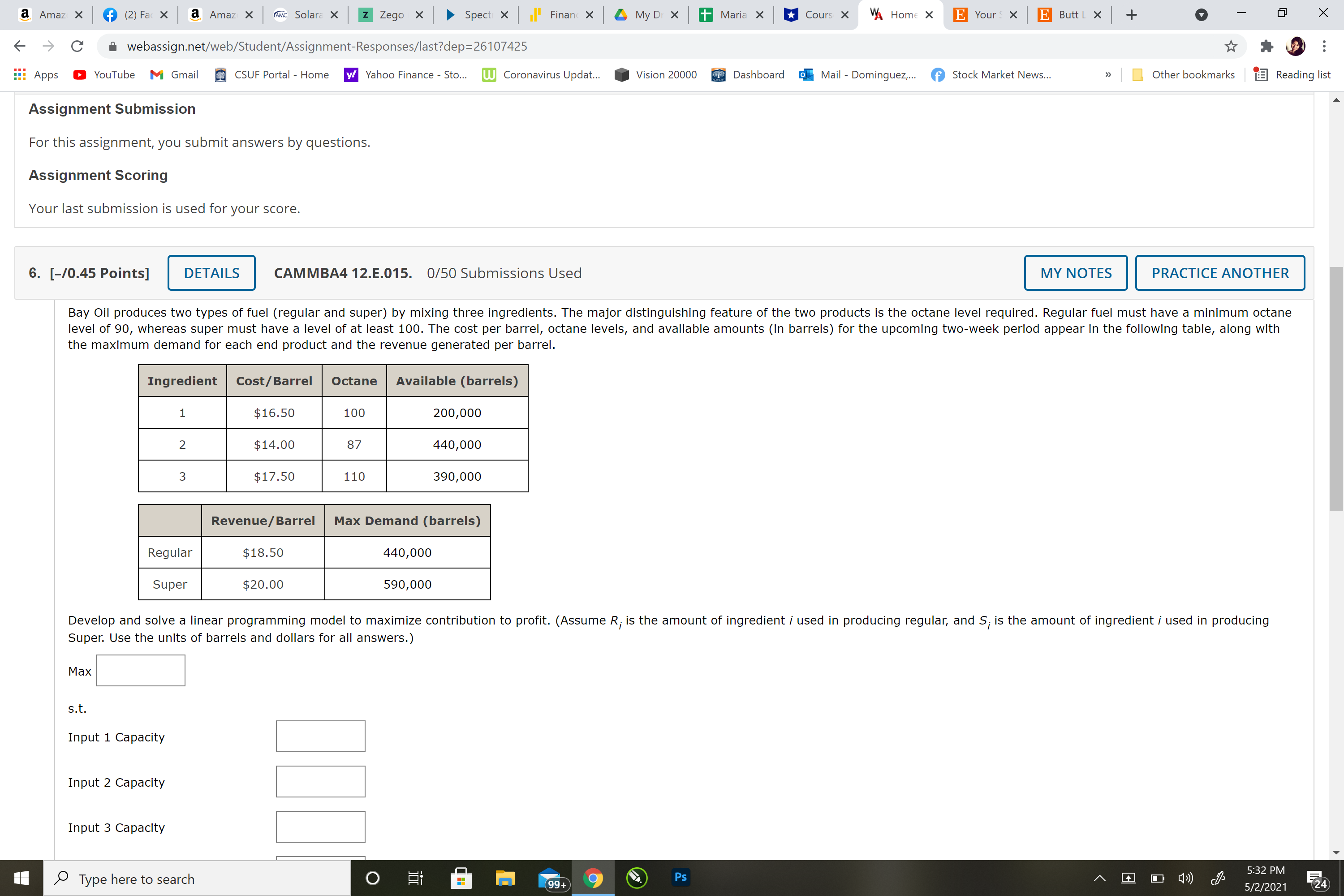
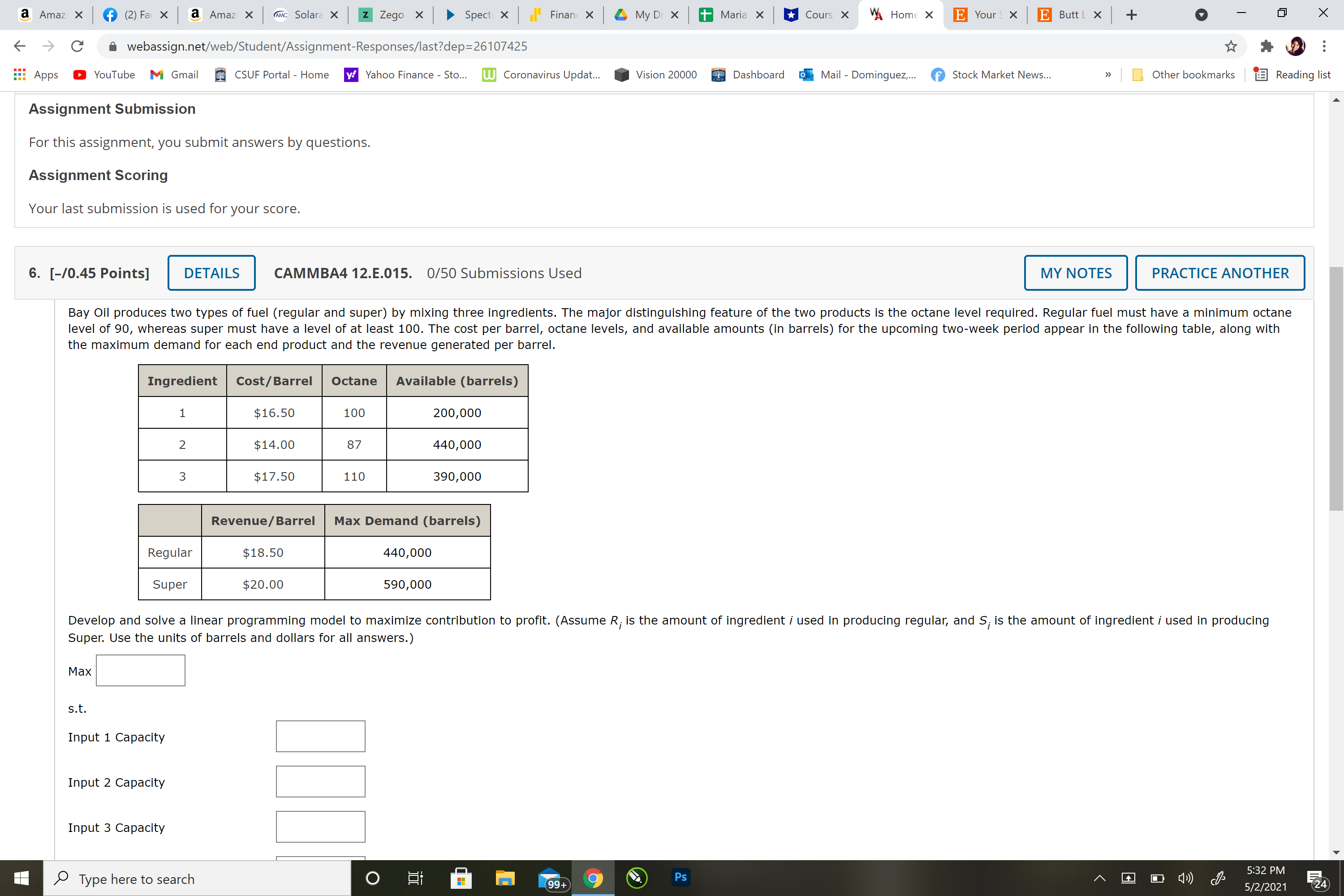
Question 6) Bay Oil produces two types of fuel (regular and super) by mixing three ingredients. The major distinguishing feature of the two products is the octane level required. Regular fuel must have a minimum octane level of 90, whereas super must have a level of at least 100. The cost per barrel, octane levels, and available amounts (in barrels) for the upcoming two-week period appear in the following table, along with the maximum demand for each end product and the revenue generated per barrel.
IngredientCost/BarrelOctaneAvailable (barrels)1$16.50100200,0002$14.0087440,0003$17.50110390,000Revenue/BarrelMax Demand (barrels)Regular$18.50440,000Super$20.00590,000
Develop and solve a linear programming model to maximize contribution to profit. (AssumeRi
is the amount of ingredientiused in producing regular, andSi
is the amount of ingredientiused in producing Super. Use the units of barrels and dollars for all answers.)
Max
s.t.Input 1 Capacity
Input 2 Capacity
Input 3 Capacity
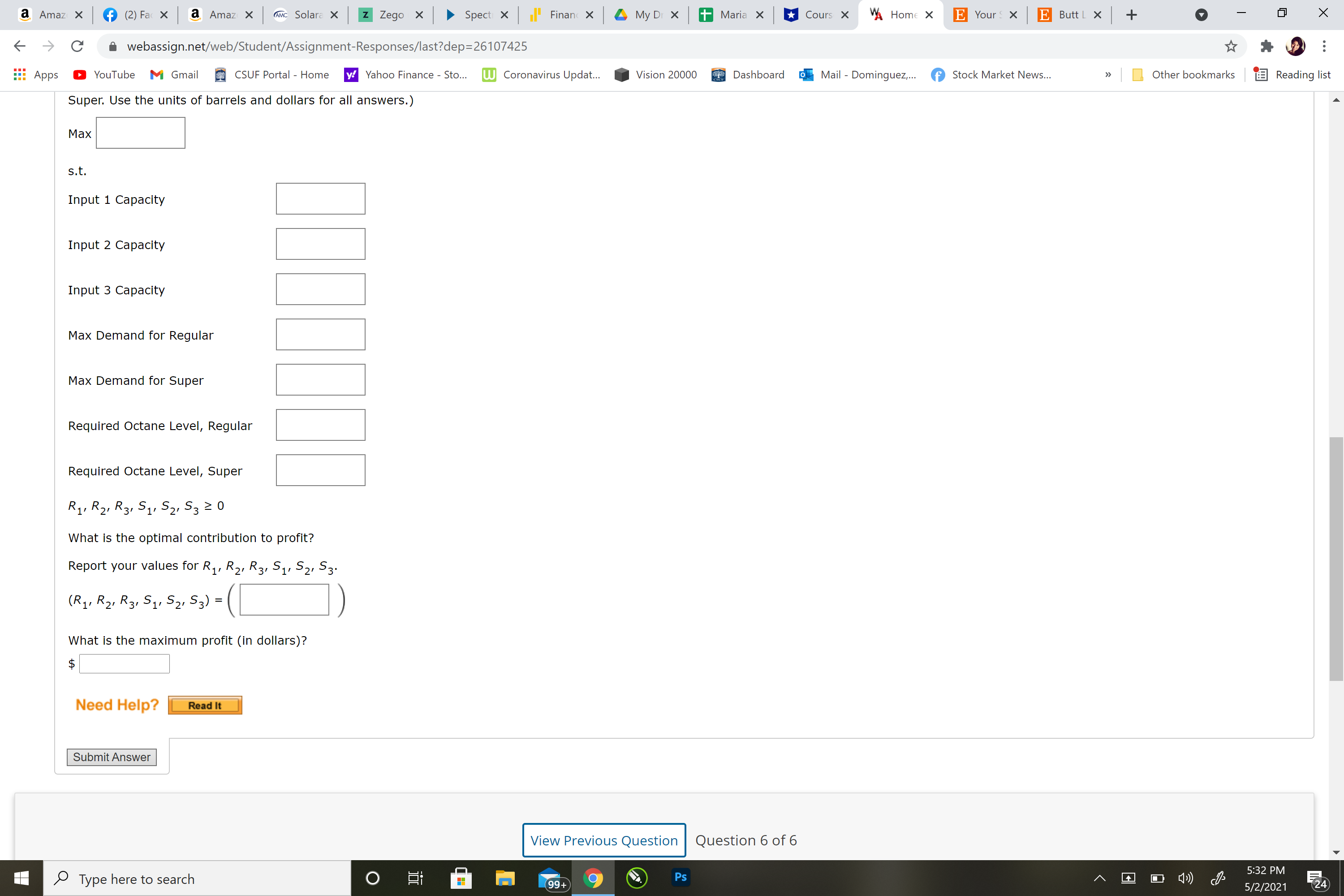
Max Demand for Regular
Max Demand for Super
Required Octane Level, Regular
Required Octane Level, Super
R1,R2,R3,S1,S2,S3?0
What is the optimal contribution to profit?
Report your values forR1,R2,R3,S1,S2,S3.
(R1,R2,R3,S1,S2,S3) =?
What is the maximum profit (in dollars)? 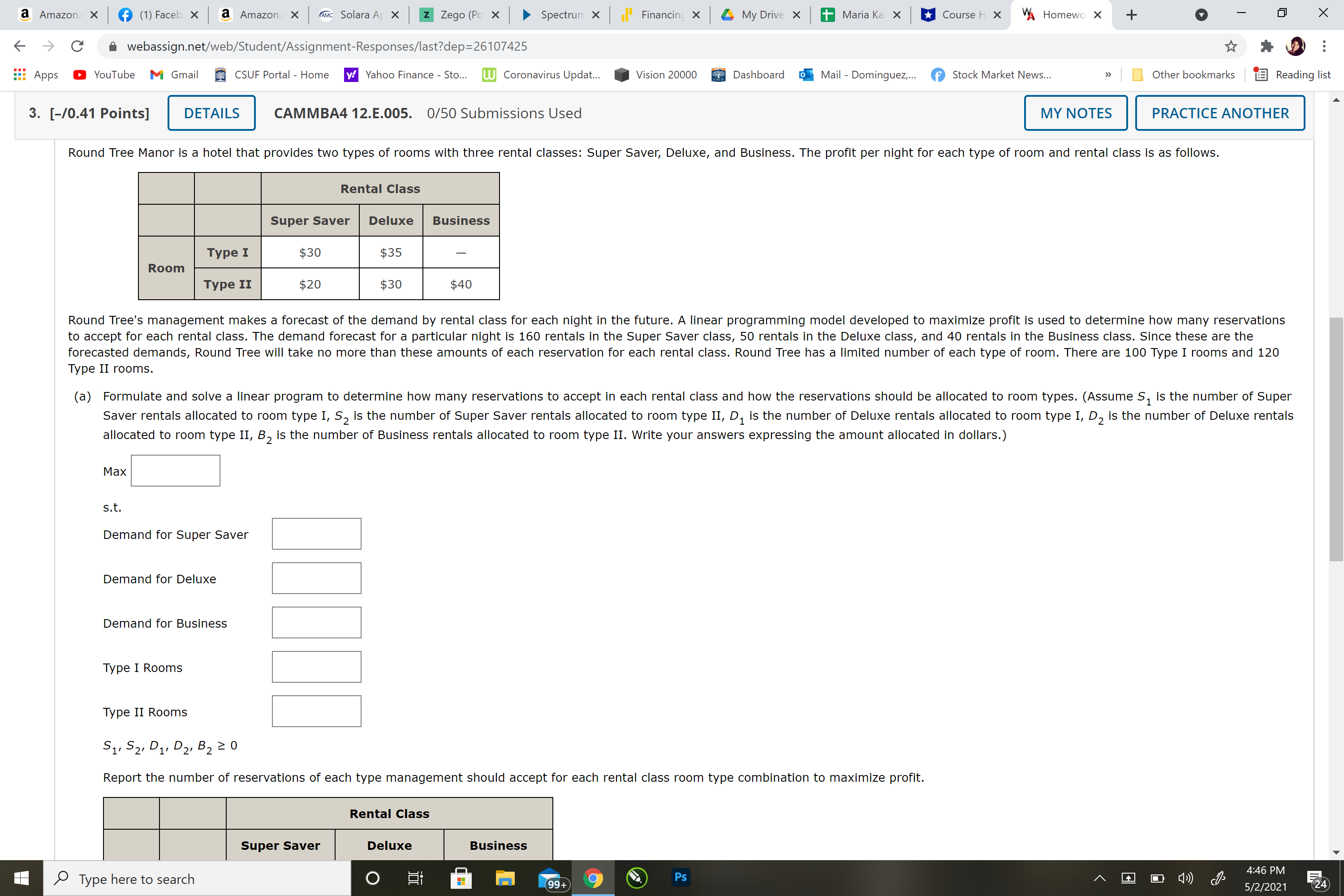
a Amazon. X f (1) Faceb x a Amazon. X AMC Solara Ap X z Zego (Po X Spectrum X | |' Financing x | My Drive x |+ Maria Ka x Course H X A Homewo X + X C webassign.net/web/Student/Assignment-Responses/last?dep=26107425 : Apps YouTube M Gmail CSUF Portal - Home y! Yahoo Finance - Sto... W Coronavirus Updat... Vision 20000 Dashboard . Mail - Dominguez,... f Stock Market News... Other bookmarks Reading list 3. [-/0.41 Points] DETAILS CAMMBA4 12.E.005. 0/50 Submissions Used MY NOTES PRACTICE ANOTHER Round Tree Manor is a hotel that provides two types of rooms with three rental classes: Super Saver, Deluxe, and Business. The profit per night for each type of room and rental class is as follows. Rental Class Super Saver Deluxe Business Type I $30 $35 Room Type II $20 $30 $40 Round Tree's management makes a forecast of the demand by rental class for each night in the future. A linear programming model developed to maximize profit is used to determine how many reservations to accept for each rental class. The demand forecast for a particular night is 160 rentals in the Super Saver class, 50 rentals in the Deluxe class, and 40 rentals in the Business class. Since these are the forecasted demands, Round Tree will take no more than these amounts of each reservation for each rental class. Round Tree has a limited number of each type of room. There are 100 Type I rooms and 120 Type II rooms. (a) Formulate and solve a linear program to determine how many reservations to accept in each rental class and how the reservations should be allocated to room types. (Assume S, is the number of Super Saver rentals allocated to room type I, S2 is the number of Super Saver rentals allocated to room type II, D, is the number of Deluxe rentals allocated to room type I, D2 is the number of Deluxe rentals allocated to room type II, B2 is the number of Business rentals allocated to room type II. Write your answers expressing the amount allocated in dollars.) Max s.t. Demand for Super Saver Demand for Deluxe Demand for Business Type I Rooms Type II Rooms 5 1, 521 D1, D2, B2 2 0 Report the number of reservations of each type management should accept for each rental class room type combination to maximize profit. Rental Class Super Saver Deluxe Business Type here to search O m Ps 4:46 PM 1994 5/2/2021a Amazon. X f Celine m X a Amazon. X AMc Solara Ap X z Zego (Po X Spectrun X | Financing X My Drive x |+ Maria Ka x Course H X VA Homewo X + X C webassign.net/web/Student/Assignment-Responses/last?dep=26107425 : Apps YouTube M Gmail CSUF Portal - Home y! Yahoo Finance - Sto... W Coronavirus Updat... Vision 20000 Dashboard . Mail - Dominguez,... f Stock Market News... "> Other bookmarks Reading list Type I Rooms Type II Rooms 51 1 52 , D1 , D2 , B 2 2 0 Report the number of reservations of each type management should accept for each rental class room type combination to maximize profit. Rental Class Super Saver Deluxe Business Type I Room Type II What is the profit (in dollars) obtained through this allocation of room reservations. $ (b) For the solution in part (a), how many reservations can be accommodated in each rental class? Super Saver Deluxe Business Is the demand for any rental class not satisfied? If demand materializes as forecast, there will be rooms not reserved in the ---Select--- v class. (c) With a little work, an unused office area could be converted to a rental room. If the conversion cost is the same for both types of rooms, would you recommend converting the office to a Type I or a Type II room? Why? ---Select--- , because this will increase profit by $ (d) Could the linear programming model be modified to plan for the allocation of rental demand for the next night? What information would be needed and how would the model change? O We would need to know if Type 1 rooms can be used as Business class rooms the next night and add a variable to the objective function. We would need to know whether the profit per night of each type of room and rental class will change and modify all the constraints appropriately. O We would need a forecast of demand for each rental class on the next night to use as the right-hand sides of the first three constraints. We would need to know how many rooms of Type I and Type II there will be on the next night to use as the right-hand sides of the last two constraints. O Eli Ps 4:46 PM Type here to search 99+ 9 5/2/2021a Amaz X f Faceb x a Amaz X AMC Solara X z Zego x Spect X |' Finan( X 4 My Di X|+ Maria x * Cours X VA Home X E Your X E Butt L x . X C webassign.net/web/Student/Assignment-Responses/last?dep=26107425 : Apps YouTube M Gmail CSUF Portal - Home y! Yahoo Finance - Sto.. W Coronavirus Updat. Vision 20000 Dashboard . Mail - Dominguez,... f Stock Market News... Other bookmarks Reading list 4. [-/0.41 Points] DETAILS CAMMBA4 12.E.008. 0/50 Submissions Used MY NOTES PRACTICE ANOTHER ;.. . . . ......... . . ............. Photon Technologies, Inc., a manufacturer of batteries for mobile phones, signed a contract with a large electronics manufacturer to produce three models of lithium-ion battery packs for a new line of phones. The contract calls for the following. Battery Pack Production Quantity PT-100 201,000 PT-200 102,000 PT-300 148,000 Photon Technologies can manufacture the battery packs at manufacturing plants located in the Philippines and Mexico. The unit cost of the battery packs differs at the two plants because of differences in production equipment and wage rates. The unit costs for each battery pack at each manufacturing plant are as follows. Product Philippines Mexico PT-100 $0.95 $0.9 PT-200 $0.98 $1.06 PT-300 $1.34 $1.15 The PT-100 and PT-200 battery packs are produced using similar production equipment available at both plants. However, each plant has a limited capacity for the total number of PT-100 and PT-200 battery packs produced. The combined PT-100 and PT-200 production capacities are 175,000 units at the Philippines plant and 160,000 units at the Mexico plant. The PT-300 production capacities are 75,000 units at the Philippines plant and 100,000 units at the Mexico plant. The cost of shipping from the Philippines plant is $0.18 per unit, and the cost of shipping from the Mexico plant is $0.10 per unit. (a) Develop a linear program that Photon Technologies can use to determine how many units of each battery pack to produce at each plant to minimize the total production and shipping cost (in dollars) associated with the new contract. (Assume P, = number of PT-100 battery packs produced at the Philippines plant, P2 = number of PT-200 battery packs produced at the Philippines plant, P3 = number of PT-300 battery packs produced at the Philippines plant, M, = number of PT-100 battery packs produced at the Mexico plant, M2 = number of PT-200 battery packs produced at the Mexico plant, M3 = number of PT-300 battery packs produced at the Mexico plant.) Min s.t. PT-100 Production PT-200 Production PT-300 Production Type here to search O 9 Ps 5:12 PM 5/2/2021a Amaz X f Faceb x a Amaz X Ac Solara X Z Zego x Spect X | |' Finan X | My Di X |+ Maria x Cours X A Home X E Yours x E Butt L x . X C webassign.net/web/Student/Assignment-Responses/last?dep=26107425 Apps YouTube M Gmail CSUF Portal - Home y! Yahoo Finance - Sto.. W Coronavirus Updat... Vision 20000 Dashboard . Mail - Dominguez,... f Stock Market News... Other bookmarks Reading list the Philippines plant and 100,000 units at the Mexico plant. The cost of shipping from the Philippines plant is $0.18 per unit, and the cost of shipping from the Mexico plant is $0.10 per unit. (a) Develop a linear program that Photon Technologies can use to determine how many units of each battery pack to produce at each plant to minimize the total production and shipping cost (in dollars) associated with the new contract. (Assume P, = number of PT-100 battery packs produced at the Philippines plant, P2 = number of PT-200 battery packs produced at the Philippines plant, P3 = number of PT-300 battery packs produced at the Philippines plant, M, = number of PT-100 battery packs produced at the Mexico plant, My = number of PT-200 battery packs produced at the Mexico plant, M3 = number of PT-300 battery packs produced at the Mexico plant.) Min s.t. PT-100 Production PT-200 Production PT-300 Production Combined PT-100 and PT-200 Production Mexico Plant Combined PT-100 and PT-200 Production Philippines Plant PT-300 Production Mexico Plant PT-300 Production Philippines Plant M1, M2' M31 P1' P21 P3 2 0 (b) Solve the linear program developed in part (a) to determine the optimal production plan. (M1 , M2, M31 P1. P2 ' P3) = What is total cost of the production plan (in dollars). (Round your answer to the nearest dollar.) $ (c) Use sensitivity analysis to determine how much the production and/or shipping cost per unit (in dollars per unit) would have to change to produce additional units of the PT-100 in the Philippines plant. It would have to decrease by more than $ per unit. (d) Use sensitivity analysis to determine how much the production and/or shipping cost per unit (in dollars per unit) would have to change to produce additional units of the PT-200 in the Mexico plant. It would have to decrease by more than $ per unit. O 5:12 PM Type here to search 99+ Ps 5/2/2021a Amaz X f Celine x a Amaz X AMC Solara X z Zego x Spect X | |' Finan X | My Di X |+ Maria x Cours X A Home X E Your s X E Butt L x . X C webassign.net/web/Student/Assignment-Responses/last?dep=26107425 Apps YouTube M Gmail CSUF Portal - Home y! Yahoo Finance - Sto... W Coronavirus Updat... Vision 20000 Dashboard . Mail - Dominguez,... f Stock Market News... "> Other bookmarks Reading list PT-300 Production Combined PT-100 and PT-200 Production Mexico Plant Combined PT-100 and PT-200 Production Philippines Plant PT-300 Production Mexico Plant PT-300 Production Philippines Plant M1, M2' M31 P1 P21 P3 2 0 (b) Solve the linear program developed in part (a) to determine the optimal production plan. (M1 , M2' M3 1 P1 . P2 . P3 ) = What is total cost of the production plan (in dollars). (Round your answer to the nearest dollar.) $ (c) Use sensitivity analysis to determine how much the production and/or shipping cost per unit (in dollars per unit) would have to change to produce additional units of the PT-100 in the Philippines plant. It would have to decrease by more than $ per unit. (d) Use sensitivity analysis to determine how much the production and/or shipping cost per unit (in dollars per unit) would have to change to produce additional units of the PT-200 in the Mexico plant. It would have to decrease by more than $ per unit. Need Help? Read It Submit Answer View Previous Question Question 4 of 6 View Next Question Type here to search O 5:12 PM 99+ Ps 5/2/2021a Amaz X f (2) Fac x a Amaz X AMC Solara X Z Zego x Spect X l' Finan X | My Di X |+ Maria x Cours X A Home X E Your s X E Butt L x X C webassign.net/web/Student/Assignment-Responses/last?dep=26107425 Apps YouTube M Gmail CSUF Portal - Home y! Yahoo Finance - Sto... W Coronavirus Updat... Vision 20000 Dashboard . Mail - Dominguez,... f Stock Market News... > Other bookmarks Reading list Assignment Submission For this assignment, you submit answers by questions. Assignment Scoring Your last submission is used for your score. 6. [-/0.45 Points] DETAILS CAMMBA4 12.E.015. 0/50 Submissions Used MY NOTES PRACTICE ANOTHER Bay Oil produces two types of fuel (regular and super) by mixing three ingredients. The major distinguishing feature of the two products is the octane level required. Regular fuel must have a minimum octane level of 90, whereas super must have a level of at least 100. The cost per barrel, octane levels, and available amounts (in barrels) for the upcoming two-week period appear in the following table, along with the maximum demand for each end product and the revenue generated per barrel. Ingredient Cost/ Barrel Octane Available (barrels) 1 $16.50 100 200,000 2 $14.00 87 440,000 3 $17.50 110 390,000 Revenue/ Barrel Max Demand (barrels) Regular $18.50 440,000 Super $20.00 590,000 Develop and solve a linear programming model to maximize contribution to profit. (Assume R, is the amount of ingredient / used in producing regular, and S, is the amount of ingredient / used in producing Super. Use the units of barrels and dollars for all answers.) Max s,t. Input 1 Capacity Input 2 Capacity Input 3 Capacity Type here to search O 9 99+ 9 Ps 5:32 PM 5/2/2021a Amaz X f (2) Fac x a Amaz X AMC Solara X Z Zego X Spect X l' Finan X 4 My Di X |+ Maria x Cours X A Home X E Your s X E Butt L x . X C webassign.net/web/Student/Assignment-Responses/last?dep=26107425 : Apps YouTube M Gmail CSUF Portal - Home y! Yahoo Finance - Sto.. W Coronavirus Updat.. Vision 20000 Dashboard . Mail - Dominguez,... f Stock Market News... "> Other bookmarks Reading list Super. Use the units of barrels and dollars for all answers. ) Max s.t Input 1 Capacity Input 2 Capacity Input 3 Capacity Max Demand for Regular Max Demand for Super Required Octane Level, Regular Required Octane Level, Super R1 , R21 R31 51 1 521 53 2 0 What is the optimal contribution to profit? Report your values for R1 , R2, R31 51, 521 53. (R1, R2, R31 51, 521 53 ) = What is the maximum profit (in dollars)? $ Need Help? Read It Submit Answer View Previous Question Question 6 of 6 Type here to search O 5:32 PM 994 Ps 5/2/2021
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


