7.1. Using risk-neutral valuation, derive a formula for a derivative that pays cash flows over the next

Fantastic news! We've Found the answer you've been seeking!

Question:

7.1. Using risk-neutral valuation, derive a formula for a derivative that pays cash flows over the next two periods. Assume the risk-free rate is 4 percent per period.

The underlying asset, which pays no cash flows unless it is sold, has a market value that is modeled in the adjacent tree diagram.

The cash flows of the derivative that correspond to the above tree diagram are

Find the present value of the derivative.

7.2. A convertible bond can be converted into a specified number of shares of stock at the option of the bondholder. Assume that a convertible bond can be converted to 1.5 shares of stock. A single share of this stock has a price that follows the binomial process

Date 0 Date 1 $80

The stock does not pay a dividend between dates 0 and 1.

If the bondholder never converts the bond to stock, the bond has a date 1 payoff of $100 + x, where x is the coupon of the bond. The conversion to stock may take place either at date 0 or date 1 (in the latter case, upon revelation of the date 1 stock price).

The convertible bond is issued at date 0 for $100. What should x, the equilibrium coupon of the convertible bond per $100 at face value, be if the risk-free return is 15 percent per period and there are no taxes, transaction costs, or arbitrage opportunities? Does the corporation save on interest payments if it issues a convertible bond in lieu of a straight bond? If so, why?

7.3. Value a risky corporate bond, assuming that the risk-free interest rate is 4 percent per period, where a period is defined as six months. The corporate bond has a face value of $100 payable two periods from now and pays a 5 percent coupon per period; that is, interest payments of $5 at the end of both the first period and the second period.

The corporate bond is a derivative of the assets of the issuing firm. Assume that the assets generate sufficient cash to pay off the promised coupon one period from now. In particular, the corporation has set aside a reserve fund of $5/1.04 per bond to pay off the promised coupon of the bond one period from now. Two periods from now, there are three possible states. In one of those states, the assets of the firm are not worth much and the firm defaults, unable to generate a sufficient amount of cash. Only $50 of the $105 promised payment is made on the bond in this state.

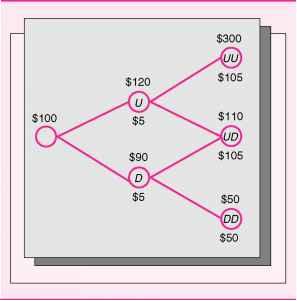
The exhibit below describes the value of the firm's assets per bond (less the amount in the reserve fund maintained for the intermediate coupon) and the cash payoffs of the bond. The nonreserved assets of the firm are currently worth $100 per bond. At the U and D nodes, the reserve fund has been depleted and the remaining assets of the firm per bond are worth $120 and $90, respectively, while they are worth $300, $110, and $50, respectively, in the UU, UD, and DD states two periods from now.

Paths for the Value of the Firm's Assets Per Bond (Above the Node) Cash Payoffs of a Risky Bond (Below the Node) in a Two-Period Binomial Tree Diagram

Callable Binomial Tree

7.4. In many instances, whether a cash flow occurs early or not is a decision of the issuer or holder of the derivative. One example of this is a callable bond, which is a bond that the issuing firm can buy back at a prespecified call price. Valuing a callable bond is complicated because the early call date is not known in advance—it depends on the future path followed by the underlying security. In these cases, it is necessary to compare the value of the security— assuming it is held a while longer—with the value obtained from cash by calling the bond or prematurely exercising the call option. To solve these problems, you must work backward in the binomial tree to make the appropriate comparisons and find the nodes in the tree where intermediate cash flows occur.

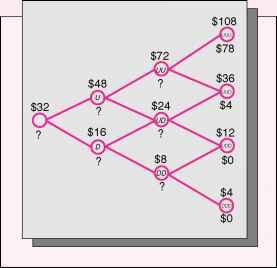
Suppose that in the absence of a call, a callable corporate bond with a call price of $100 plus accrued interest has cash flows identical to those of the bond in exercise 7.3. (In this case, accrued interest is the $5 coupon if it is called cum-coupon at the intermediate date and 0 if it is called excoupon.) What is the optimal call policy of the issuing firm, assuming that the firm is trying to maximize shareholder wealth? What is the value of the callable bond? Hint: Keep in mind that maximizing shareholder wealth is the same as minimizing the value of the bond. 7.5. Consider a stock that can appreciate by 50 percent or depreciate by 50 percent per period. Three periods from now, a stock with an initial value of $32 per share can be worth (1) $108—three up moves; (2) $36—two up moves, one down move;

(4) $4—three down moves. Three periods from now, a derivative is worth $78 in case (1), $4 in case (2), and $0 otherwise. If the risk-free rate is 10 percent throughout these three periods, describe a portfolio of the stock and a risk-free bond that tracks the payoff of the derivative and requires no future cash outlays. Then, fill in the question marks in the accompanying exhibit, which illustrates the paths of the stock and the derivative. Hint: You need to work backward. Use the risk-neutral valuation method to check your work.

Three-Period Binomial Tree Diagram Underlying Security's Price Above Node, Derivative's Price Below Node

Risk Neutral Valuation

7.6. Consider a forward contract on IBM requiring purchase of a share of IBM stock for $150 in six months. The stock currently sells for $140 a share. Assume that it pays no dividends over the coming six months. Six-month zero-coupon bonds are selling for $98 per $100 of face value.

a. If the forward is selling for $10.75, is there an arbitrage opportunity? If so, describe exactly how you could take advantage of it.

b. Assume that three months from now: (i) the stock price has risen to $160 and (ii) three-month zero-coupon bonds are selling for $99. How much has the fair market value of your forward contract changed over the three months that have elapsed?

7.7. Assume that forward contracts to purchase one share of Sony and Disney for $100 and $40, respectively, in one year are currently selling for $3.00 and $2.20. Assume that neither stock pays a dividend over the coming year and that one-year zero-coupon bonds are selling for $93 per $100 of face value. The current prices of Sony and Disney are $90 and $35, respectively.

a. Are there any arbitrage opportunities? If so, describe how to take advantage of them.

b. What is the fair market price of a forward contract on a portfolio composed of one-half share of Sony and one-half share of Disney, requiring that $70 be paid for the portfolio in one year?

c. Is this the same as buying one-half of a forward contract on each of Sony and Disney? Why or why not? (Show payoff tables.)

d. Is it generally true that a forward on a portfolio is the same as a portfolio of forwards? Explain.

7.8. Assume the Eurodollar rate (nine-month LIBOR) is

9 percent and the Eurosterling rate (nine-month LIBOR for the U.K. currency) is 11 percent. What is the nine-month forward $/£ exchange rate if the current spot exchange rate is $1.58/£? (Assume that nine months from now is 274 days.)

7.9. Assume that futures prices for Hewlett-Packard (HP) can appreciate by 15 percent or depreciate by

10 percent and that the risk-free rate is 10 percent over the next period. Price a derivative security on HP that has payoffs of $25 in the up state and 2$5 in the down state in the next period, where the actual probability of the up state occurring is 75 percent.

7.10. A stock price follows a binomial process for two periods. In each period, it either increases by 20 percent or decreases by 20 percent. Assuming that the stock pays no dividends, value a derivative which at the end of the second period pays $10 for every up move of the stock that occurred over the previous two periods. Assume that the risk-free rate is 6 percent per period.

7.11. A stock has a 30% per year standard deviation of its logged returns. If you are modeling the stock price to value a derivative maturing in six months with eight binomial periods, what should u and d be?

7.12. Find the risk neutral probabilities and zero cost date 0 forward prices (for settlement at date 1) for the stock in exercise 7.2. As in that exercise, assume a risk-free rate of 15% per period.

7.13. A European "Tootsie Square" is a financial contract, which, at maturity, pays off the square of the price of the underlying stock on which it is written. For instance, if the price of the underlying stock is $3 at maturity, the Tootsie Square contract pays off $9. Consider a two period Tootsie Square written on ABC stock.