Answered step by step
Verified Expert Solution
Question
1 Approved Answer
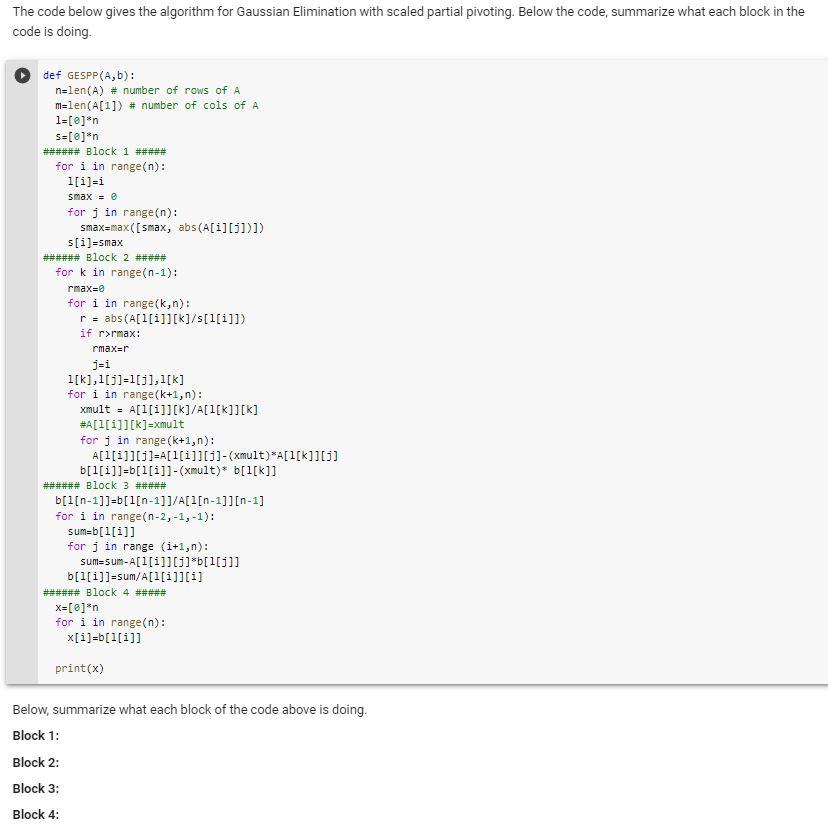
The code below gives the algorithm for Gaussian Elimination with scaled partial pivoting. Below the code, summarize what each block in the code is doing.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


