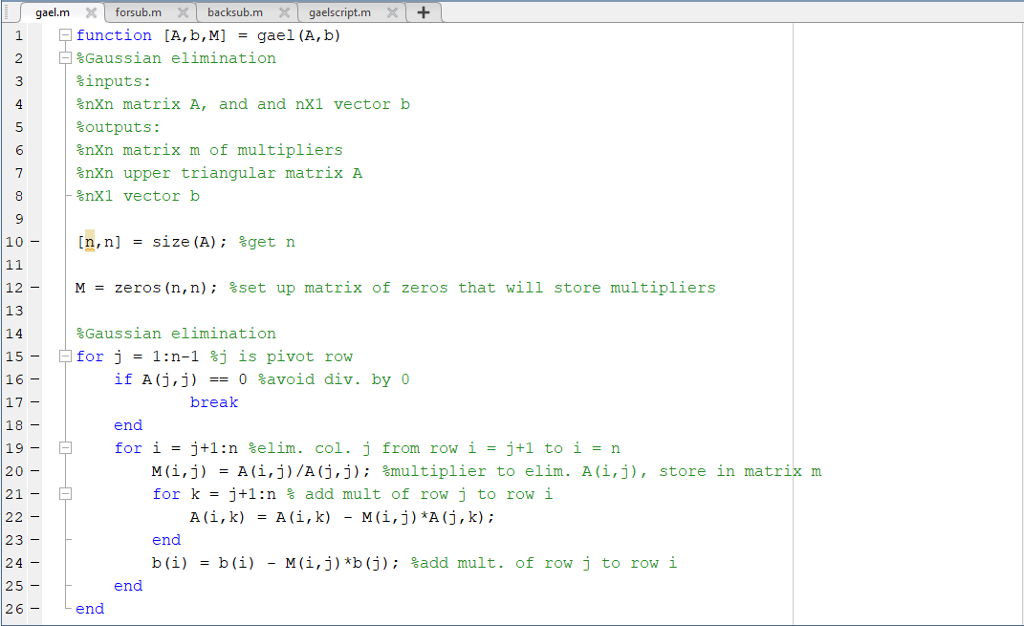
The code provided for gael.m is as follows:

function [A,b,M] = gael(A,b) %Gaussian elimination %inputs: %nXn matrix A, and and nX1 vector b %outputs: %nXn matrix m of multipliers %nXn upper triangular matrix A %nX1 vector b

[n,n] = size(A); %get n

M = zeros(n,n); %set up matrix of zeros that will store multipliers

%Gaussian elimination for j = 1:n-1 %j is pivot row if A(j,j) == 0 %avoid div. by 0 break end for i = j+1:n %elim. col. j from row i = j+1 to i = n M(i,j) = A(i,j)/A(j,j); %multiplier to elim. A(i,j), store in matrix m for k = j+1:n % add mult of row j to row i A(i,k) = A(i,k) - M(i,j)*A(j,k); end b(i) = b(i) - M(i,j)*b(j); %add mult. of row j to row i end end

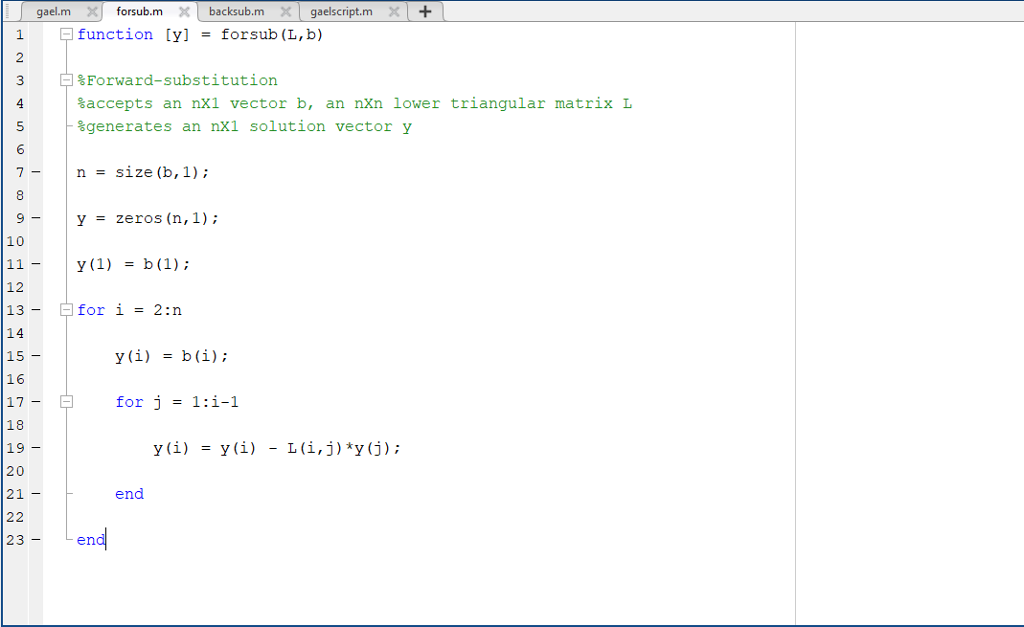
The code provided for forsub.m is as follows:

function [y] = forsub(L,b)

%Forward-substitution %accepts an nX1 vector b, an nXn lower triangular matrix L %generates an nX1 solution vector y

n = size(b,1);

y = zeros(n,1);

y(1) = b(1);

for i = 2:n y(i) = b(i); for j = 1:i-1 y(i) = y(i) - L(i,j)*y(j); end end

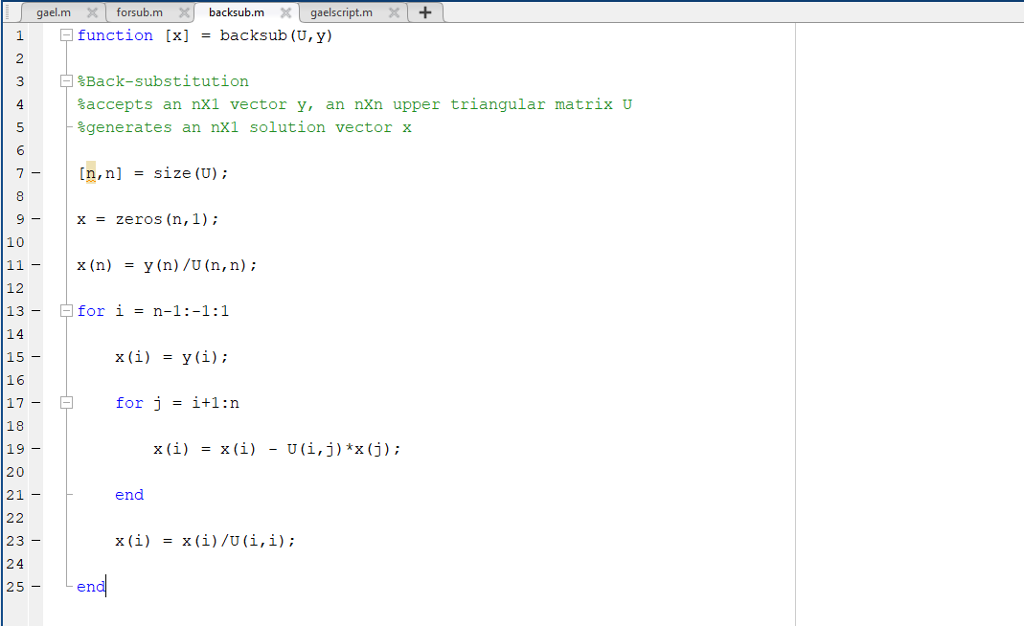
The code provided for backsub.m is as follows:

function [x] = backsub(U,y) %Back-substitution %accepts an nX1 vector y, an nXn upper triangular matrix U %generates an nX1 solution vector x

[n,n] = size(U); x = zeros(n,1); x(n) = y(n)/U(n,n);

for i = n-1:-1:1 x(i) = y(i); for j = i+1:n x(i) = x(i) - U(i,j)*x(j); end x(i) = x(i)/U(i,i); end

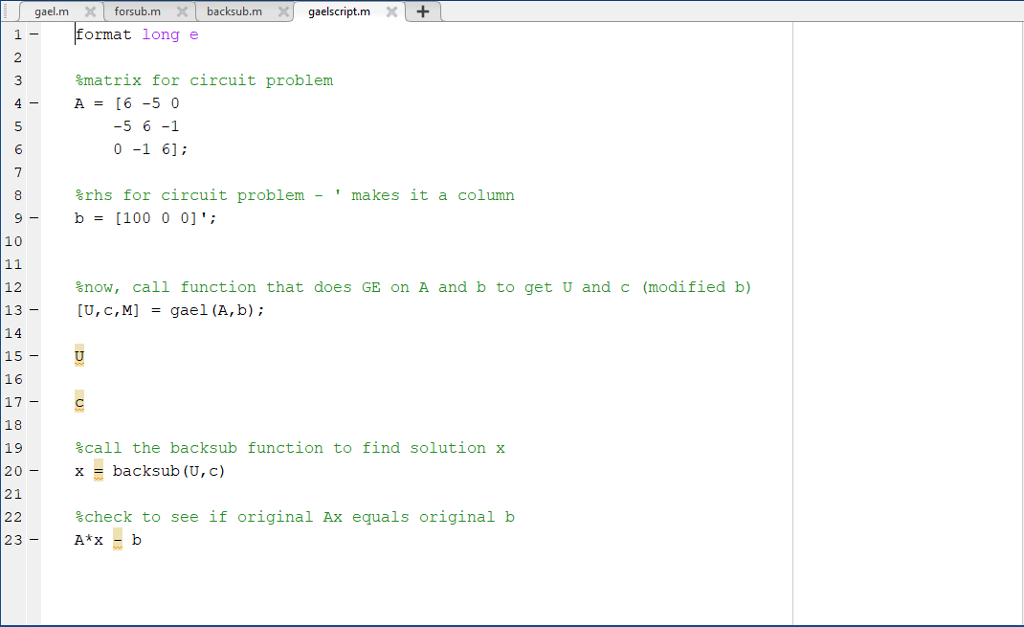
The code provided for gaelscript.m is as follows:

format long e

%matrix for circuit problem A = [6 -5 0 -5 6 -1 0 -1 6];

%rhs for circuit problem - ' makes it a column b = [100 0 0]';

%now, call function that does GE on A and b to get U and c (modified b) [U,c,M] = gael(A,b);

U

c

%call the backsub function to find solution x x = backsub(U,c)

%check to see if original Ax equals original b A*x - b

MATLAB Problems: 1) In this problem, you will convert a function that performs GE (Gaussian Elimination) to one that performs GEPP (Gaussian Elimination with Partial Pivoting) a) Modify the function gael.m (posted in eLearning), so that it accepts only the A matrix a:s input, and produces only two outputs. One output will be the modified (overwritten) version of A, which contains the multipliers in the lower triangular portion, along with the upper triangular matrix generated by GEPP. The other output will be the n x n permutation matrix P also generated during GEPP. Call your modified function gaelpp.m so that the first line is function [A,P] = gaeipp(A) Hints . You can use the MATLAB function eye() to initialize P. . The MATLAB function ALU-max(A(j:nJ)) will return an index 1 for the location of the maximum value of the column vector Aj:nj). Note that you will need to adjust this index and also use the absolute value To swap rows, it will help to use a variable temp to temporarily store a row vector You will also need to swap rows of P accordingly. You need to overwrite appropriate entries of A with the multipliers instead of saving them in M. . . b) Write a script gaelppscript.m to test your function from part (a). Use 3.03 -12.1 14 A3.03 12.1-7 6.11 -14.2 21 and b120 139 This script will also call the functions forsub.m and backsub.m with appropriate inputs (also provided in eLearning). Display your computed solution. You do not need to use any loops in this script c) Now, replace the matrix A and right-hand side b in gaelscript.m (given in eLearning) with the matrix and right-hand side defined in part (b) (Gaussian elimination without partial pivoting). Run this script and print out your results. Compare to your results from part (b) MATLAB Problems: 1) In this problem, you will convert a function that performs GE (Gaussian Elimination) to one that performs GEPP (Gaussian Elimination with Partial Pivoting) a) Modify the function gael.m (posted in eLearning), so that it accepts only the A matrix a:s input, and produces only two outputs. One output will be the modified (overwritten) version of A, which contains the multipliers in the lower triangular portion, along with the upper triangular matrix generated by GEPP. The other output will be the n x n permutation matrix P also generated during GEPP. Call your modified function gaelpp.m so that the first line is function [A,P] = gaeipp(A) Hints . You can use the MATLAB function eye() to initialize P. . The MATLAB function ALU-max(A(j:nJ)) will return an index 1 for the location of the maximum value of the column vector Aj:nj). Note that you will need to adjust this index and also use the absolute value To swap rows, it will help to use a variable temp to temporarily store a row vector You will also need to swap rows of P accordingly. You need to overwrite appropriate entries of A with the multipliers instead of saving them in M. . . b) Write a script gaelppscript.m to test your function from part (a). Use 3.03 -12.1 14 A3.03 12.1-7 6.11 -14.2 21 and b120 139 This script will also call the functions forsub.m and backsub.m with appropriate inputs (also provided in eLearning). Display your computed solution. You do not need to use any loops in this script c) Now, replace the matrix A and right-hand side b in gaelscript.m (given in eLearning) with the matrix and right-hand side defined in part (b) (Gaussian elimination without partial pivoting). Run this script and print out your results. Compare to your results from part (b)