The coding language is MATLAB It should be solvable with for, while, and if statements

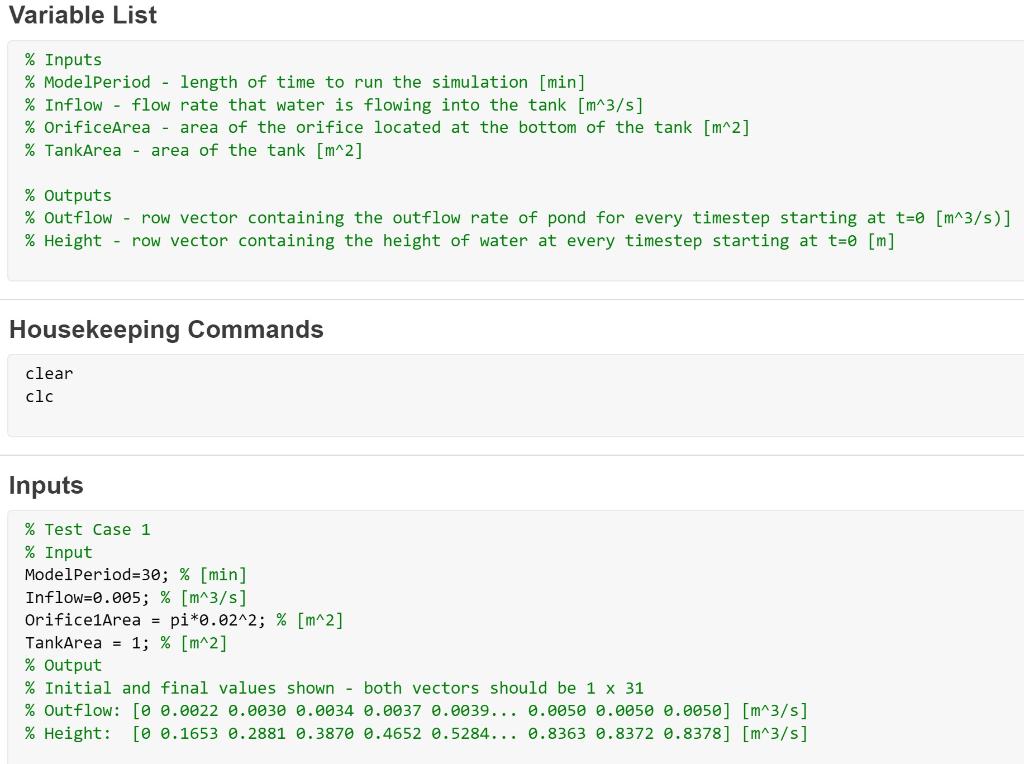
Problem Statement This lab is going to model the water level in a tank as it water is simultaneously flowing in and out. You can visualize this as a bathtub that has the water running but the drain open. If the water is flowing in faster than it is draining, the water level will rise, if it is flowing in slower than it is draining the water level will fall, and if the inflow and outflow are equal, the water level will remain constant. The length of time to be modeled, the inflow rate, tank area, and the drain outlet size will be given as inputs from MATLAB Grader. You will model the system with a time step of 1 min which means that you will calculate the height of water and the outflow rate from the tank for every minute from time zero to the length of time to be modeled. You can assume that the contain is empty at the beginning of the time (i.e., height of water is zero at time zero) and therefore there is no outflow at time zero. Below is the procedure for calculating the outflow and height of water for a single time step: Outflow and Height of Water Since the water height and outflow depend on each other, we cannot estimate one without knowing the other. This is an implicit problem, so we will need to make an initial guess and then iterate until successive answers are nearly the same. Therefore, use the height of the water in the tank from the previous time step as your initial estimate to calculate the outflow, then use that calculated outflow to calculate the new height. Repeat the calculations until the difference between the height input into the equations and the height output from the equations is less than or equal to 0.01 m. Outflow The contain is drained by an orifice (hole) at the bottom of the tank. Outflow is dependent on the water pressure (and consequently the depth of water). The flowrate, Q, for a single orifice is Q = (0.98) A 2gh where Aorifice is the area of the orifice, g is the gravitational acceleration, and h is the height of water above the orifice. Using standard Sl units, area in square meters, gravity in meters per seconds squared, and the height in meters, the outflow will be in cubic meters per second. Height of Water Height of Water The change in water volume over time can be calculated with the following equation: Volume Rate = dV dt Inflow - Outflow The dv/dt represents the change in volume of water in the tank over time in units of cubic meters per second. This equation simply represents the concept that if more water is coming in than leaving, the volume of water and therefore the height) increases (positive Volume Rate). If more water is leaving than coming in, the volume (and therefore the height) decreases (negative Volume Rate). Multiplying dv/dt by the time step will give us the change in volume over the time step, and dividing that by the area of the tank will give the change in height over the time step (the difference between the height at the previous time step (hi-1) and the height at the current time step (h;)). As an equation rearranged to solve for the height of water at the current time step this would be: dV (timestep) dt h; = hi-1 + Area Pond These two equations can be combined to solve for the height of water at the current time step (h;). Note that the height of water at the previous time step (h;-1) is should remain constant during the iterative solution process - the height that is converging is the height at the current time step. Due to approximation errors, it is possible for the height be calculated as a negative value when the tank is almost empty. Because this is physically impossible, check the height value calculated by these equations and if it is negative, set the height to be zero instead. Once the height has converged (the absolute difference between the input height and output height is less than 0.01 m), make sure that you store the outflow [m^3/s] and height [m] values in the vectors Outflow and Height respectively. Variable List % Inputs % ModelPeriod - length of time to run the simulation [min] % Inflow - flow rate that water is flowing into the tank [m^3/s] % OrificeArea - area of the orifice located at the bottom of the tank [m^2] % TankArea - area of the tank [m2] % Outputs % Outflow - row vector containing the outflow rate of pond for every timestep starting at t=0 [m^3/s)] % Height - row vector containing the height of water at every timestep starting at t=0 [m] Housekeeping Commands clear clc Inputs % Test Case 1 % Input ModelPeriod=30; % [min] Inflow=0.005; % [m^3/s] Orifice1Area = pi*0.02^2; % [m^2] TankArea = 1; % [m^2] % Output % Initial and final values shown - both vectors should be 1 x 31 % Outflow: [0 0.0022 0.0030 0.0034 0.0037 0.0039... 0.0050 0.0050 0.0050] [m^3/5] % Height: [0 0.1653 0.2881 0.3870 0.4652 0.5284... 0.8363 0.8372 0.8378] [m^3/s] Inputs % Test Case 1 % Input ModelPeriod=30; % [min] Inflow=0.005; % [m^3/s] Orifice1Area = pi*0.02^2; % [m^2] TankArea = 1; % [m^2] % Output % Initial and final values shown - both vectors should be 1 x 31 % Outflow: [0 0.0022 0.0030 0.0034 0.0037 0.0039... 0.0050 0.0050 0.0050] [m^3/s] % Height: [ 0.1653 0.2881 0.3870 0.4652 0.5284... 0.8363 0.8372 0.8378] [m^3/s] % % Test Case 2 % % Input % ModelPeriod=60; % [min] % Inflow=0.03; % [m^3/s] % Orifice1Area = pi*0.05^2; % [m^2] % TankArea = 12; % [m^2] % % Output % % Initial and final values shown - both vectors should be 1 x 61 % % Outflow: [0 0.0108 0.0141 0.0137 0.0186 0.0203... 0.0300 0.0300 0.0300] [m^3/s] % % Height: [o 0.0960 0.1755 0.2421 0.2992 0.3475... 0.7731 0.7733 0.7735] [m^3/s] % % Test Case 3 % % Input % ModelPeriod=120; % [min] % Inflow=0.4; % [m^3/s] % Orifice1Area = pi*0.1^2; % [m^2] % TankArea = 50; % [m^2] % % Output % % Initial and final values shown - both vectors should be 1 x 121 % % Outflow: [0 0.0841 0.1154 0.1385 0.1569 0.1723... 0.3940 0.3941 0.3943] [m^3/s] % % Height: [0 0.3790 0.7206 1.0344 1.3262 1.5994... 8.3617 8.3687 8.3756] [m^3/s] Problem Statement This lab is going to model the water level in a tank as it water is simultaneously flowing in and out. You can visualize this as a bathtub that has the water running but the drain open. If the water is flowing in faster than it is draining, the water level will rise, if it is flowing in slower than it is draining the water level will fall, and if the inflow and outflow are equal, the water level will remain constant. The length of time to be modeled, the inflow rate, tank area, and the drain outlet size will be given as inputs from MATLAB Grader. You will model the system with a time step of 1 min which means that you will calculate the height of water and the outflow rate from the tank for every minute from time zero to the length of time to be modeled. You can assume that the contain is empty at the beginning of the time (i.e., height of water is zero at time zero) and therefore there is no outflow at time zero. Below is the procedure for calculating the outflow and height of water for a single time step: Outflow and Height of Water Since the water height and outflow depend on each other, we cannot estimate one without knowing the other. This is an implicit problem, so we will need to make an initial guess and then iterate until successive answers are nearly the same. Therefore, use the height of the water in the tank from the previous time step as your initial estimate to calculate the outflow, then use that calculated outflow to calculate the new height. Repeat the calculations until the difference between the height input into the equations and the height output from the equations is less than or equal to 0.01 m. Outflow The contain is drained by an orifice (hole) at the bottom of the tank. Outflow is dependent on the water pressure (and consequently the depth of water). The flowrate, Q, for a single orifice is Q = (0.98) A 2gh where Aorifice is the area of the orifice, g is the gravitational acceleration, and h is the height of water above the orifice. Using standard Sl units, area in square meters, gravity in meters per seconds squared, and the height in meters, the outflow will be in cubic meters per second. Height of Water Height of Water The change in water volume over time can be calculated with the following equation: Volume Rate = dV dt Inflow - Outflow The dv/dt represents the change in volume of water in the tank over time in units of cubic meters per second. This equation simply represents the concept that if more water is coming in than leaving, the volume of water and therefore the height) increases (positive Volume Rate). If more water is leaving than coming in, the volume (and therefore the height) decreases (negative Volume Rate). Multiplying dv/dt by the time step will give us the change in volume over the time step, and dividing that by the area of the tank will give the change in height over the time step (the difference between the height at the previous time step (hi-1) and the height at the current time step (h;)). As an equation rearranged to solve for the height of water at the current time step this would be: dV (timestep) dt h; = hi-1 + Area Pond These two equations can be combined to solve for the height of water at the current time step (h;). Note that the height of water at the previous time step (h;-1) is should remain constant during the iterative solution process - the height that is converging is the height at the current time step. Due to approximation errors, it is possible for the height be calculated as a negative value when the tank is almost empty. Because this is physically impossible, check the height value calculated by these equations and if it is negative, set the height to be zero instead. Once the height has converged (the absolute difference between the input height and output height is less than 0.01 m), make sure that you store the outflow [m^3/s] and height [m] values in the vectors Outflow and Height respectively. Variable List % Inputs % ModelPeriod - length of time to run the simulation [min] % Inflow - flow rate that water is flowing into the tank [m^3/s] % OrificeArea - area of the orifice located at the bottom of the tank [m^2] % TankArea - area of the tank [m2] % Outputs % Outflow - row vector containing the outflow rate of pond for every timestep starting at t=0 [m^3/s)] % Height - row vector containing the height of water at every timestep starting at t=0 [m] Housekeeping Commands clear clc Inputs % Test Case 1 % Input ModelPeriod=30; % [min] Inflow=0.005; % [m^3/s] Orifice1Area = pi*0.02^2; % [m^2] TankArea = 1; % [m^2] % Output % Initial and final values shown - both vectors should be 1 x 31 % Outflow: [0 0.0022 0.0030 0.0034 0.0037 0.0039... 0.0050 0.0050 0.0050] [m^3/5] % Height: [0 0.1653 0.2881 0.3870 0.4652 0.5284... 0.8363 0.8372 0.8378] [m^3/s] Inputs % Test Case 1 % Input ModelPeriod=30; % [min] Inflow=0.005; % [m^3/s] Orifice1Area = pi*0.02^2; % [m^2] TankArea = 1; % [m^2] % Output % Initial and final values shown - both vectors should be 1 x 31 % Outflow: [0 0.0022 0.0030 0.0034 0.0037 0.0039... 0.0050 0.0050 0.0050] [m^3/s] % Height: [ 0.1653 0.2881 0.3870 0.4652 0.5284... 0.8363 0.8372 0.8378] [m^3/s] % % Test Case 2 % % Input % ModelPeriod=60; % [min] % Inflow=0.03; % [m^3/s] % Orifice1Area = pi*0.05^2; % [m^2] % TankArea = 12; % [m^2] % % Output % % Initial and final values shown - both vectors should be 1 x 61 % % Outflow: [0 0.0108 0.0141 0.0137 0.0186 0.0203... 0.0300 0.0300 0.0300] [m^3/s] % % Height: [o 0.0960 0.1755 0.2421 0.2992 0.3475... 0.7731 0.7733 0.7735] [m^3/s] % % Test Case 3 % % Input % ModelPeriod=120; % [min] % Inflow=0.4; % [m^3/s] % Orifice1Area = pi*0.1^2; % [m^2] % TankArea = 50; % [m^2] % % Output % % Initial and final values shown - both vectors should be 1 x 121 % % Outflow: [0 0.0841 0.1154 0.1385 0.1569 0.1723... 0.3940 0.3941 0.3943] [m^3/s] % % Height: [0 0.3790 0.7206 1.0344 1.3262 1.5994... 8.3617 8.3687 8.3756] [m^3/s]