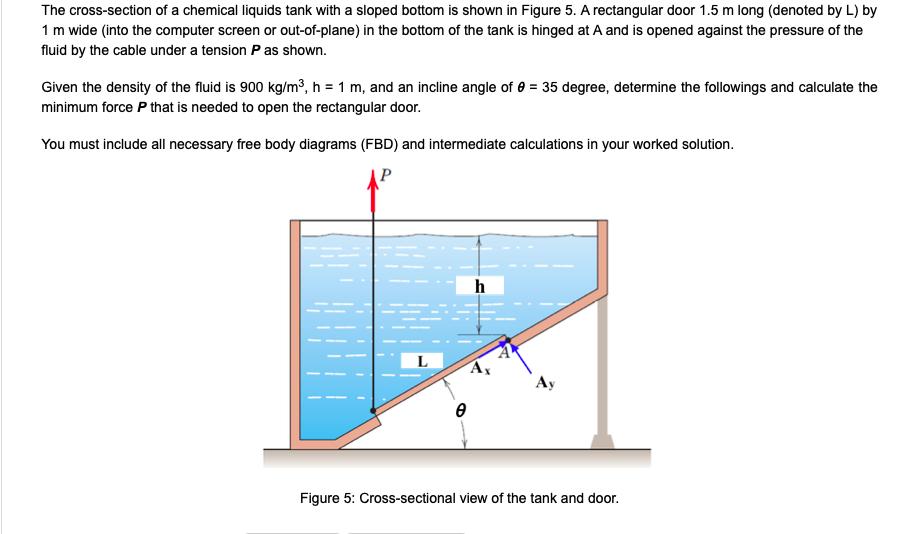
The cross-section of a chemical liquids tank with a sloped bottom is shown in Figure 5. A rectangular door 1.5 m long (denoted by L) by 1 m wide (into the computer screen or out-of-plane) in the bottom of the tank is hinged at A and is opened against the pressure of the fluid by the cable under a tension P as shown. Given the density of the fluid is 900 kg/m, h = 1 m, and an incline angle of 0 = 35 degree, determine the followings and calculate the minimum force P that is needed to open the rectangular door. You must include all necessary free body diagrams (FBD) and intermediate calculations in your worked solution. L e Figure 5: Cross-sectional view of the tank and door. fluid pressure at point A = Number Units total vertical force by fluid acting on the door = Number (tolerance of 1 N/m^2) (1 mark) Units marks) total horizontal force by fluid acting on the door = Number (4 marks) Units (magnitude only; tolerance of 1 N) (3 (magnitude only; tolerance of 1 N) resultant force by fluid acting on the door = Number Units Units reaction Ax (positive direction indicated by blue arrow) = Number N) (2 marks) reaction A, (positive direction indicated by blue arrow) = Number N) (2 marks) minimum force P = Number Units Units (magnitude only; tolerance of 1 N) (4 marks) (include sign; tolerance of 1 (include sign; tolerance of 1 (magnitude only; tolerance of 1 N) (4 marks)