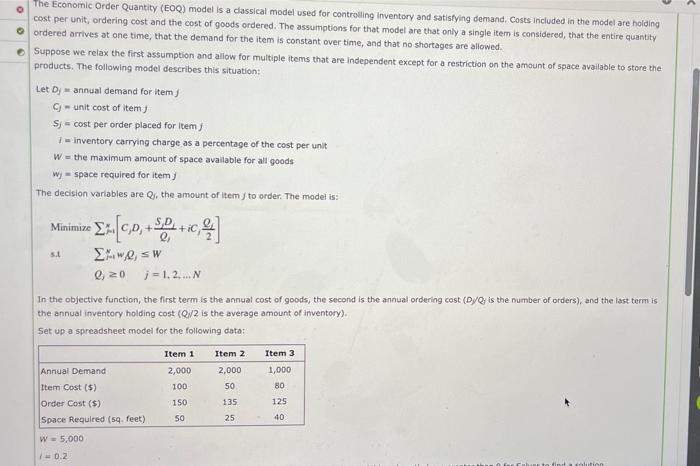
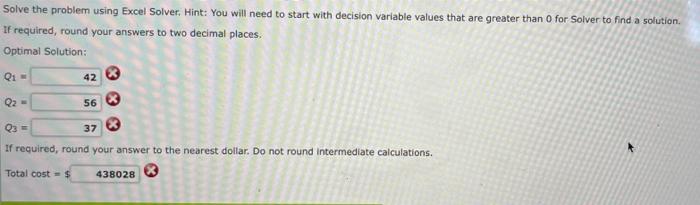
The Economic Order Quantity (E0Q) model is a classical model used for controlling inventory and satisfying demand. Costs included in the model are holding cost per unit, ordering cost and the cost of goods ordered. The assumptions for that model are that only a single item is considered, that the entire quantity o ordered arrives at one time, that the demand for the item is constant over time, and that no shortages are allowed. Suppose we relax the first assumption and allow for multiple items that are independent except for a restriction on the amount of space available to store the products. The following model describes this situation: Let Dj - annual demand for Items g -unit cost of item S; - cost per order placed for Item 1 = Inventory carrying charge as a percentage of the cost per unit W = the maximum amount of space available for all goods Wyspace required for item The decision variables are Qs, the amount of item to order. The model is: Minimize iC 2*[0,0,+S.+16,9] xwe, sw 5.1 0,20 j = 1.2.... In the objective function, the first term is the annual cost of goods, the second is the annual ordering cost (D/Q; is the number of orders), and the last term is the annual inventory holding cost (Q/2 is the average amount of inventory) Set up a spreadsheet model for the following datar Item 1 Item 2 Item 3 Annual Demand 2,000 100 2,000 50 1,000 80 Item Cost (5) Order Cost (5) Space Required (5 feet) 150 125 135 25 so 40 W = 5,000 0.2 Solve the problem using Excel Solver. Hint: You will need to start with decision variable values that are greater than o for Solver to find a solution. If required, round your answers to two decimal places. Optimal Solution: Q: - 42 Q2 = 56 Q3 = 37 If required, round your answer to the nearest dollar. Do not round Intermediate calculations. Total cost $ 438028 8 The Economic Order Quantity (E0Q) model is a classical model used for controlling inventory and satisfying demand. Costs included in the model are holding cost per unit, ordering cost and the cost of goods ordered. The assumptions for that model are that only a single item is considered, that the entire quantity o ordered arrives at one time, that the demand for the item is constant over time, and that no shortages are allowed. Suppose we relax the first assumption and allow for multiple items that are independent except for a restriction on the amount of space available to store the products. The following model describes this situation: Let Dj - annual demand for Items g -unit cost of item S; - cost per order placed for Item 1 = Inventory carrying charge as a percentage of the cost per unit W = the maximum amount of space available for all goods Wyspace required for item The decision variables are Qs, the amount of item to order. The model is: Minimize iC 2*[0,0,+S.+16,9] xwe, sw 5.1 0,20 j = 1.2.... In the objective function, the first term is the annual cost of goods, the second is the annual ordering cost (D/Q; is the number of orders), and the last term is the annual inventory holding cost (Q/2 is the average amount of inventory) Set up a spreadsheet model for the following datar Item 1 Item 2 Item 3 Annual Demand 2,000 100 2,000 50 1,000 80 Item Cost (5) Order Cost (5) Space Required (5 feet) 150 125 135 25 so 40 W = 5,000 0.2 Solve the problem using Excel Solver. Hint: You will need to start with decision variable values that are greater than o for Solver to find a solution. If required, round your answers to two decimal places. Optimal Solution: Q: - 42 Q2 = 56 Q3 = 37 If required, round your answer to the nearest dollar. Do not round Intermediate calculations. Total cost $ 438028 8