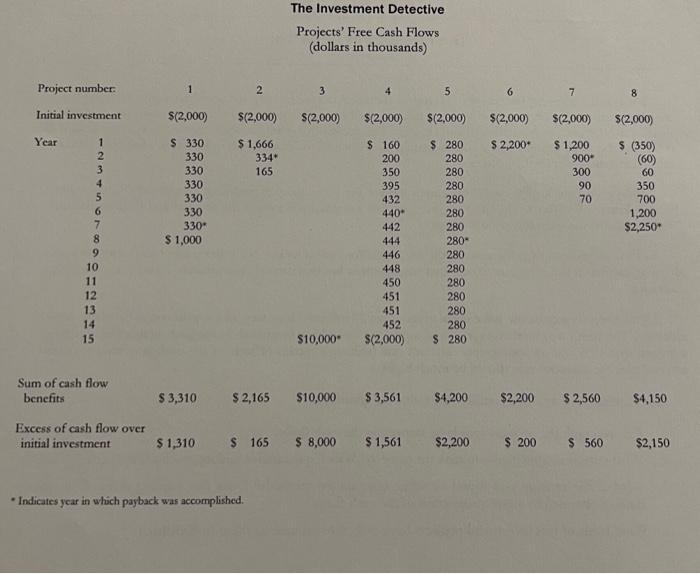
The essence of capital budgeting and resource allocation is a search for good investments in which to place the firm's capital. The process can be simple when viewed in purely mechanical terms, but a number of subtle issues can obscure the best investment choices. The capital-budgeting analyst, therefore, is necessarily a detective who must winnow bad evidence from good. Much of the challenge is in knowing what quantitative analysis to generate in the first place. Suppose you are a new capital-budgeting analyst for a company considering investments in the eight projects listed in Exhibit 1 The CFO of your company has asked you to rank the projects and recommend the "four best" that the company should accept In this assignment, only the quantitative considerations are relevant. No other project characteristics are deciding factors in the selection, except that management has determined that projects 7 and 8 are mutually exclusive All the projects require the same initial investment, $2 million. Moreover, all are believed to be of the san risk class. The firm's weighted average cost of capital has never been estimated. In the past, analysts have simply assumed that 10% was an appropriate discount rate (although certain officers of the company have recently asserted that the discount rate should be much higher). To stimulate your analysis, consider the following questions: 1. Can you rank the projects simply by inspecting the cash flows? 2. What criteria might you use to rank the projects? Which quantitative ranking methods are better? Why? 3. What is the ranking you found by using quantitative methods? Does this ranking differ from the ranking obtained by simple inspection of the cash flows? 4. What kinds of real investment projects have cash flows similar to those in Exhibit 1? The Investment Detective Projects' Free Cash Flows (dollars in thousands) Project number: 1 2 3 4 5 6 7 8 Initial investment $(2,000) $(2,000) S(2,000) $(2,000) $(2,000) $(2,000) $(2,000) $(2,000) Year $ 2,200 $ (350) $1,666 334 165 (60) 1 2 3 4 5 6 $ 330 330 330 330 330 330 330" $1,000 $ 1,200 900- 300 90 70 60 350 700 1,200 $2,250 8 9 10 11 12 13 14 15 $ 160 200 350 395 432 440 442 444 446 448 450 451 451 452 $(2.000) $ 280 280 280 280 280 280 280 280- 280 280 280 280 280 280 $ 280 $10,000 Sum of cash flow benefits $ 3,310 $ 2,165 $10,000 $3,561 $4,200 $2,200 $ 2,560 $4,150 Excess of cash flow over initial investment $ 1,310 $ 165 $8,000 $ 1,561 $2,200 $ 200 S 560 $2,150 Indicates year in which payback was accomplished. 1. Before doing any calculations, can we rank the projects simply by inspecting the cash flows? Can you use this method to select projects, why or why not? quod bent Please logo 2. What decision rules can be used to rank and select amongst the projects? Which ranking methods are better? Why? Hint: List the investment decision rules we covered in class, the advantages and disadvantages of each. 3. 3 Rank the projects using the four decision rules covered in class. Show your work 4. Projects 7 and 8 are mutually exclusive. a) Which of the two projects, 7 or 8, is more attractive? b) How sensitive is your ranking to the use of high discount rates? Hint: Calculate NPV with more than one discount rate for both projects. c) Why do NPV and IRR disagree? 5. Does the ranking in #3 above differ from the ranking obtained by simple inspection of the cash flows in #1 above? 6. Why do payback and NPV not agree completely on rankings? What ranking will you use and why? 7. Are those projects comparable since they have different lives? If not, calculate the equivalent Annual Annuity for each project. 8. . What kinds of real investment projects have cash flows similar to those in Exhibit 1