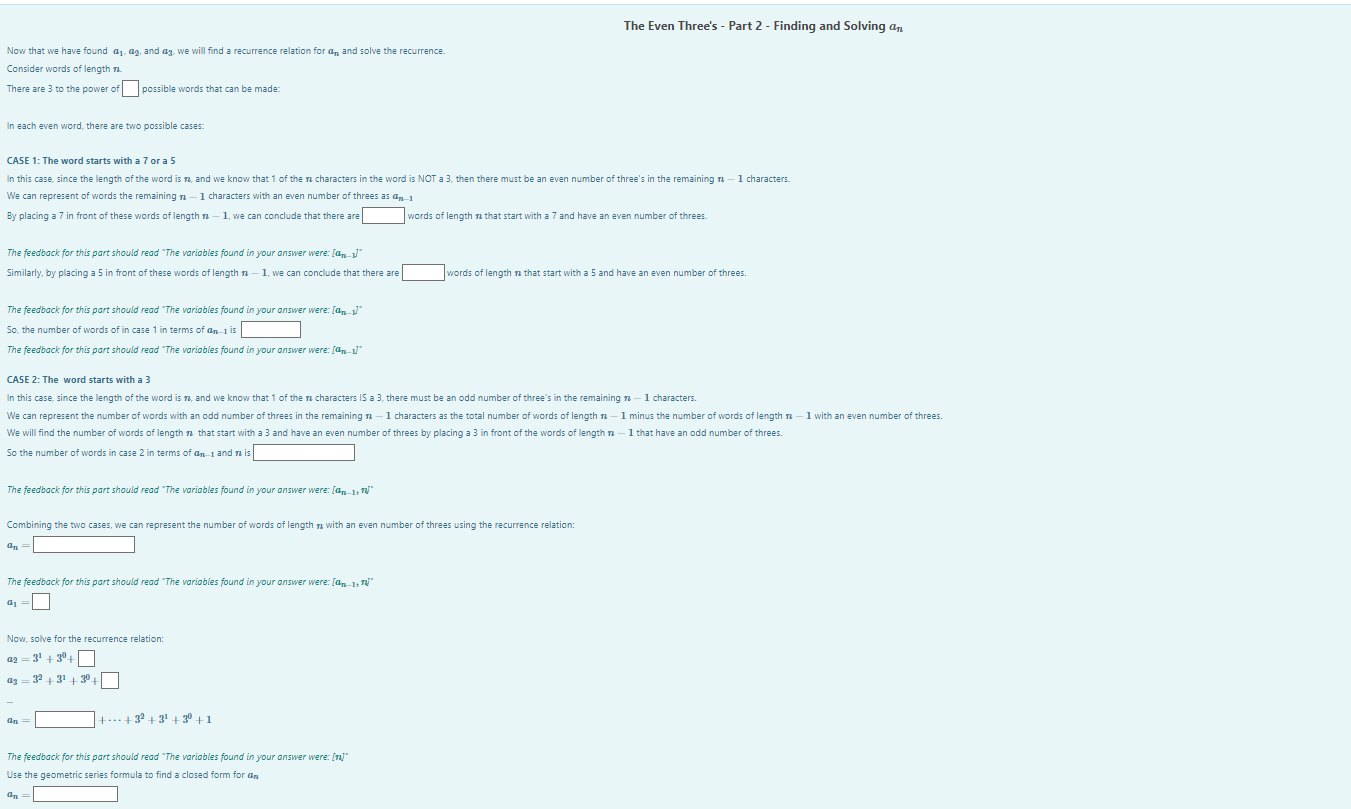
The Even Three's - Part 2 - Finding and Solving an Now that we have found 4. Qg, and ag, we will find a recurrence relation for an and solve the recurrence Consider words of length There are 3 to the power of possible words that can be made: In each even word, there are two possible cases: CASE 1: The word starts with a 7 or a 5 In this case, since the length of the word is n and we know that 1 of the n characters in the word is NOT a 3, then there must be an even number of three's in the remaining n - 1 characters. We can represent of words the remaining n - 1 characters with an even number of threes Q-1 By placing a 7 in front of these words of length 7 1, we can conclude that there are words of length that start with a 7 and have even number of threes. The feedback for this part should read "The variables found in your answer were [an]" Similarly, by placing a 5 in front of these words of length - 1, we can conclude that there are words of length n that start with a 5 and have an even number of threes. The feedback for this part should read "The variables found in your answer were [an]" So, the number of words of in case 1 in terms of an- is The feedback for this part should read "The variables found in your answer were: fan-11 CASE 2: The word starts with a 3 In this case, since the length of the word is n, and we know that 1 of the n characters 15 a 3, there must be an odd number of three's in the remaining 1-1 characters. We can represent the number of words with an odd number of threes in the remaining n - 1 characters as the total number of words of length n - 1 minus the number of words of length n - 1 with an even number of threes. We will find the number of words of length n that start with a 3 and have an even number of threes by placing a 3 in front of the words of length n - 1 that have an odd number threes. So the number of words in case 2 in terms of an-1 and rais The feedback for this part should read "The variables found in your answer were: lan-1,7 Combining the two cases, we can represent the number of words F length rz with an even number of threes using the recurrence relation: an The feedback for this part should read "The variables found in your answer were: [an-1,741 au Now, solve for the recurrence relation: 02 31 +30+ a = 32 +31 an + ... +39 +31 +3 + 1 The feedback for this part should read "The variobles found in your answer were: [ra]" Use the geometric series formula to find a closed form for an The Even Three's - Part 2 - Finding and Solving an Now that we have found 4. Qg, and ag, we will find a recurrence relation for an and solve the recurrence Consider words of length There are 3 to the power of possible words that can be made: In each even word, there are two possible cases: CASE 1: The word starts with a 7 or a 5 In this case, since the length of the word is n and we know that 1 of the n characters in the word is NOT a 3, then there must be an even number of three's in the remaining n - 1 characters. We can represent of words the remaining n - 1 characters with an even number of threes Q-1 By placing a 7 in front of these words of length 7 1, we can conclude that there are words of length that start with a 7 and have even number of threes. The feedback for this part should read "The variables found in your answer were [an]" Similarly, by placing a 5 in front of these words of length - 1, we can conclude that there are words of length n that start with a 5 and have an even number of threes. The feedback for this part should read "The variables found in your answer were [an]" So, the number of words of in case 1 in terms of an- is The feedback for this part should read "The variables found in your answer were: fan-11 CASE 2: The word starts with a 3 In this case, since the length of the word is n, and we know that 1 of the n characters 15 a 3, there must be an odd number of three's in the remaining 1-1 characters. We can represent the number of words with an odd number of threes in the remaining n - 1 characters as the total number of words of length n - 1 minus the number of words of length n - 1 with an even number of threes. We will find the number of words of length n that start with a 3 and have an even number of threes by placing a 3 in front of the words of length n - 1 that have an odd number threes. So the number of words in case 2 in terms of an-1 and rais The feedback for this part should read "The variables found in your answer were: lan-1,7 Combining the two cases, we can represent the number of words F length rz with an even number of threes using the recurrence relation: an The feedback for this part should read "The variables found in your answer were: [an-1,741 au Now, solve for the recurrence relation: 02 31 +30+ a = 32 +31 an + ... +39 +31 +3 + 1 The feedback for this part should read "The variobles found in your answer were: [ra]" Use the geometric series formula to find a closed form for an