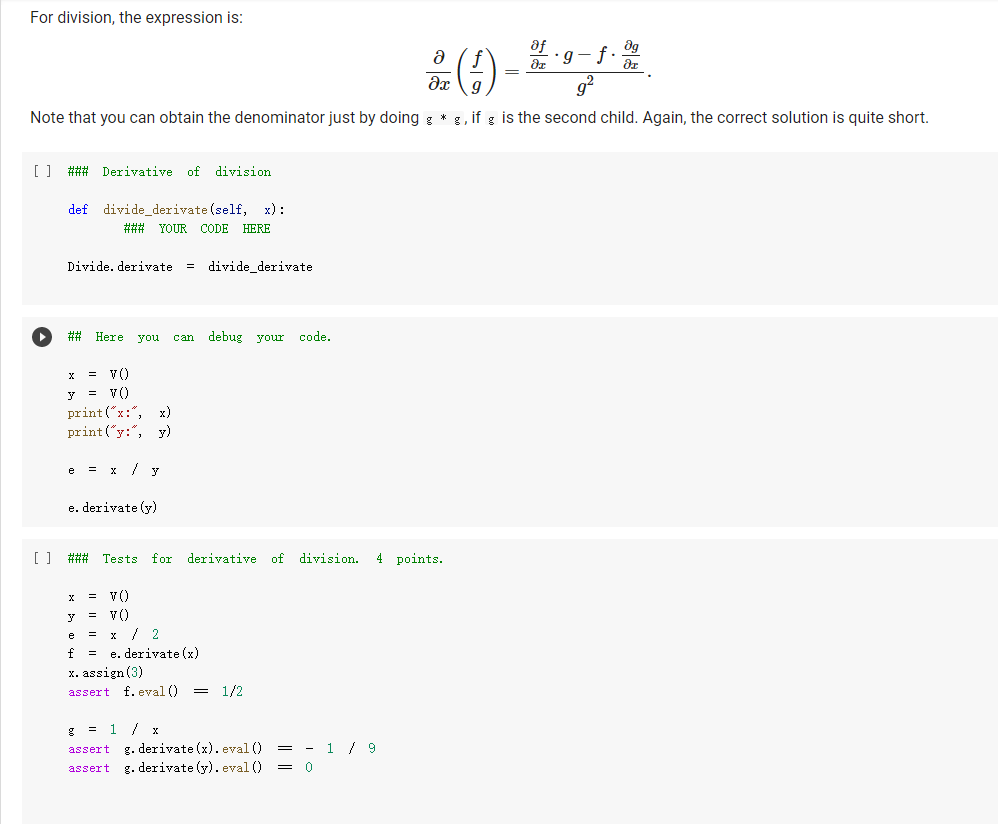
Question: The Expr class The Expr class implements the various methods used to emulate numerical types, such as _add_, _sub_, and so forth. In this way,
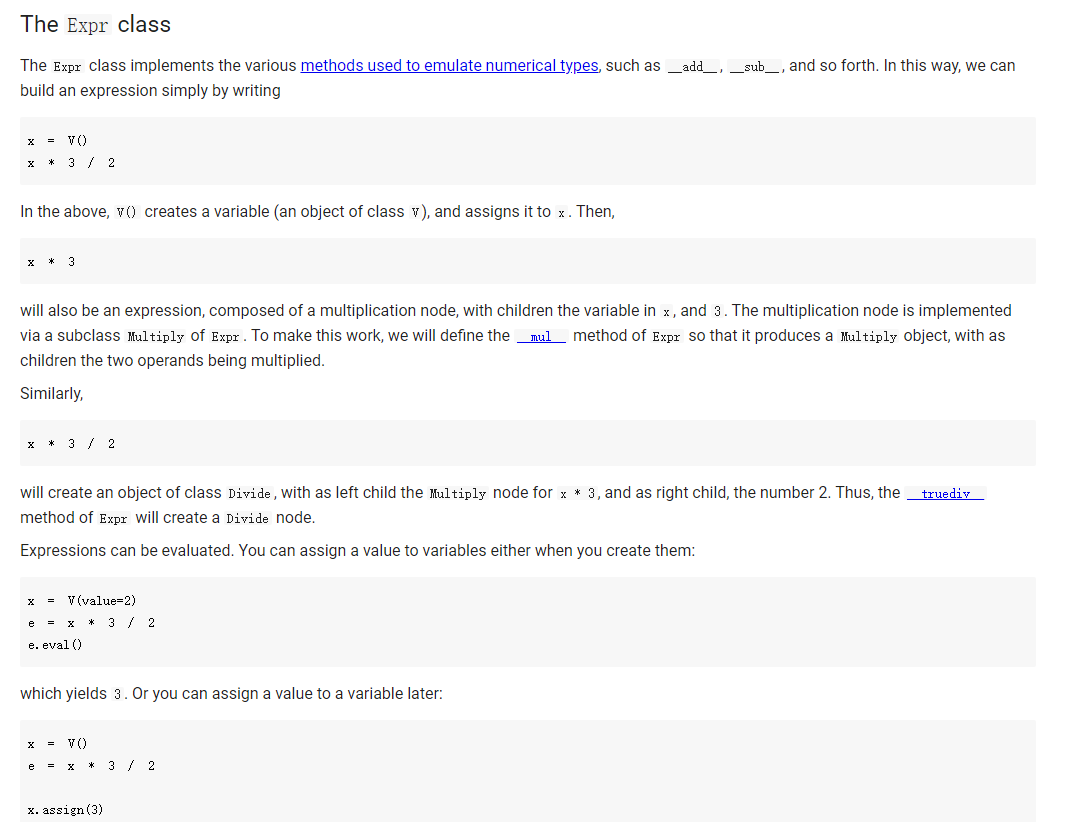

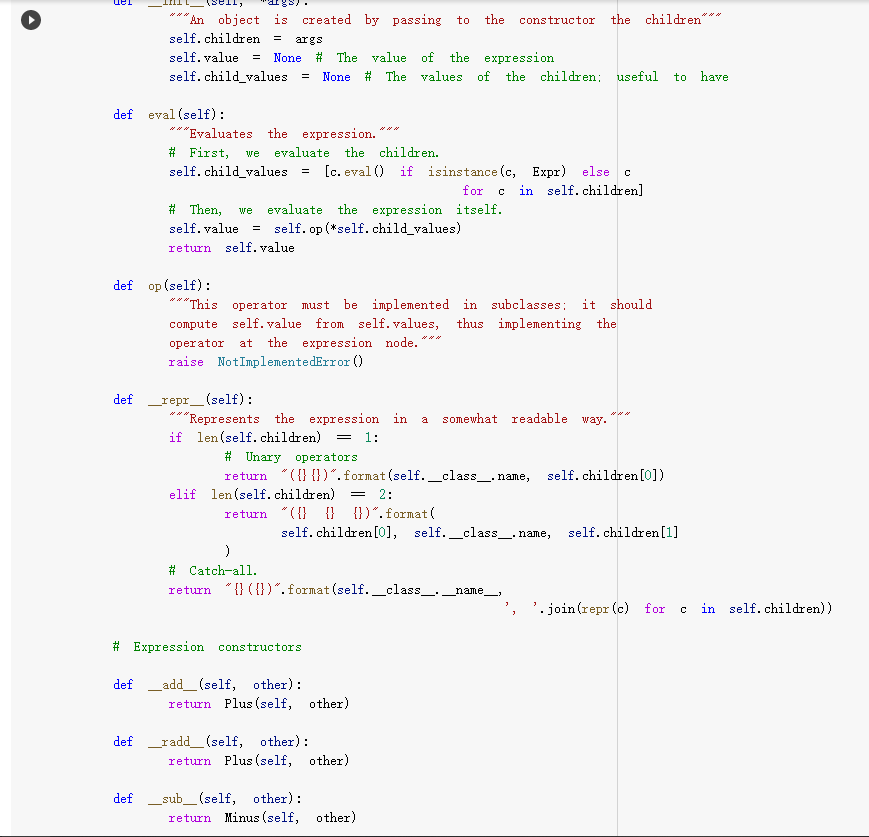

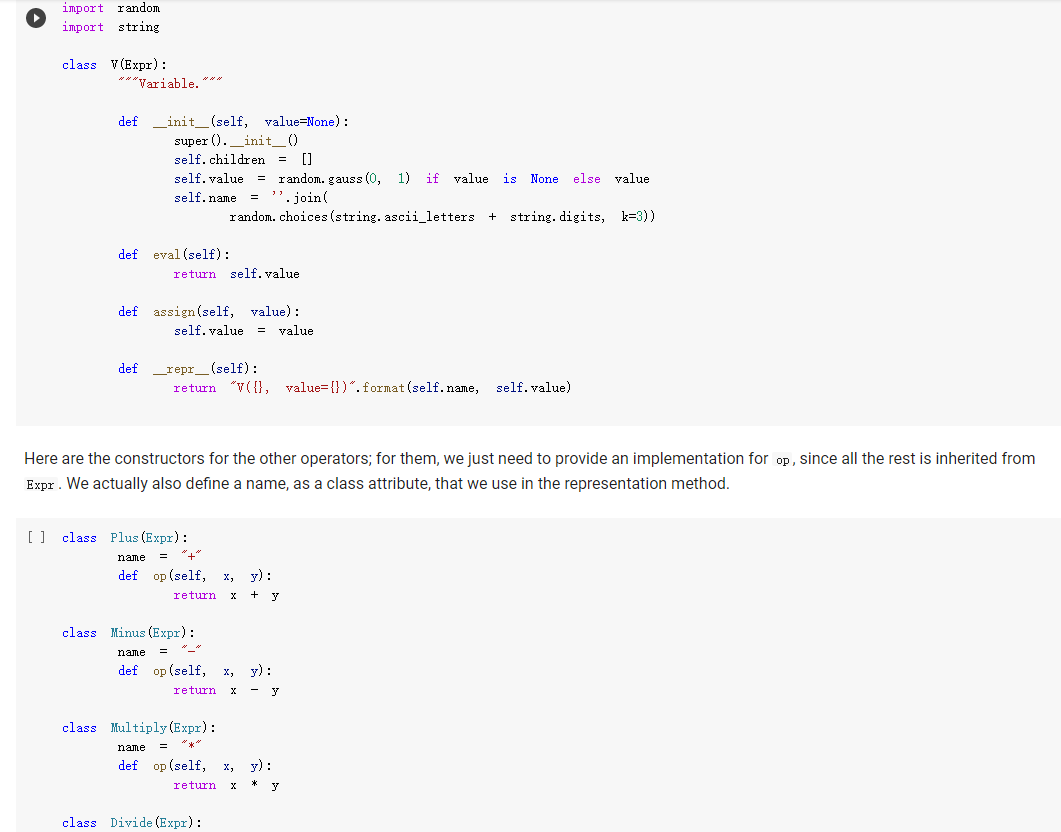
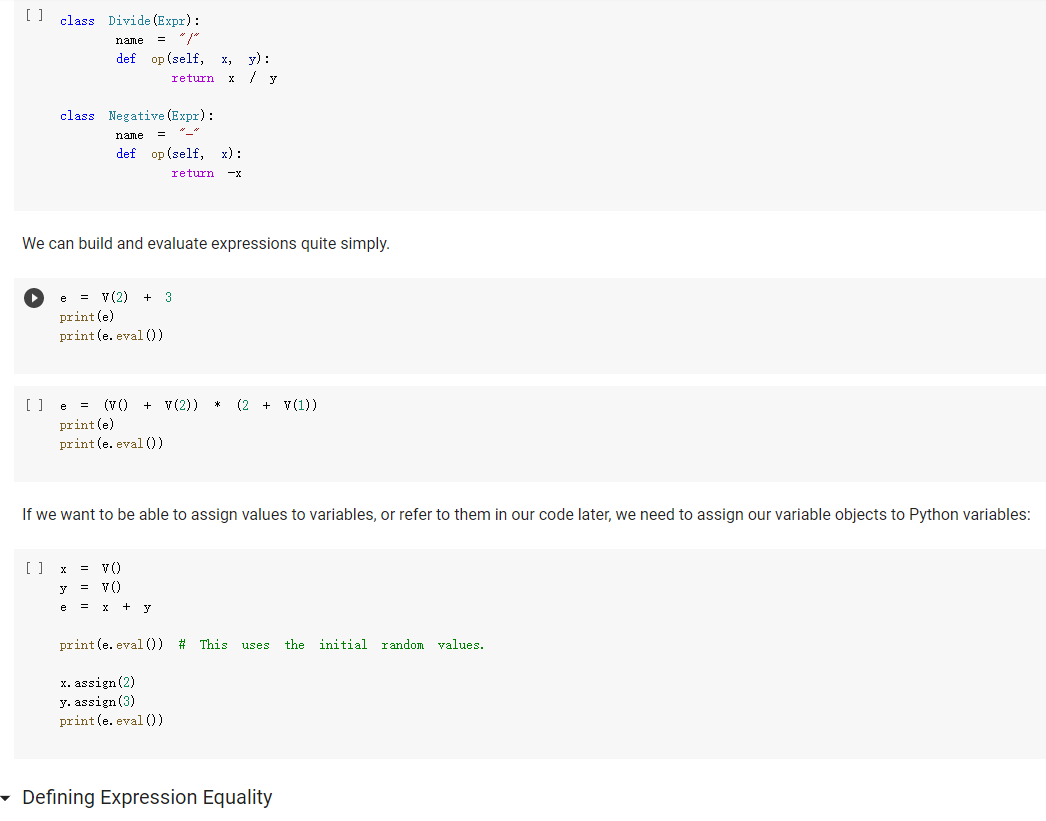
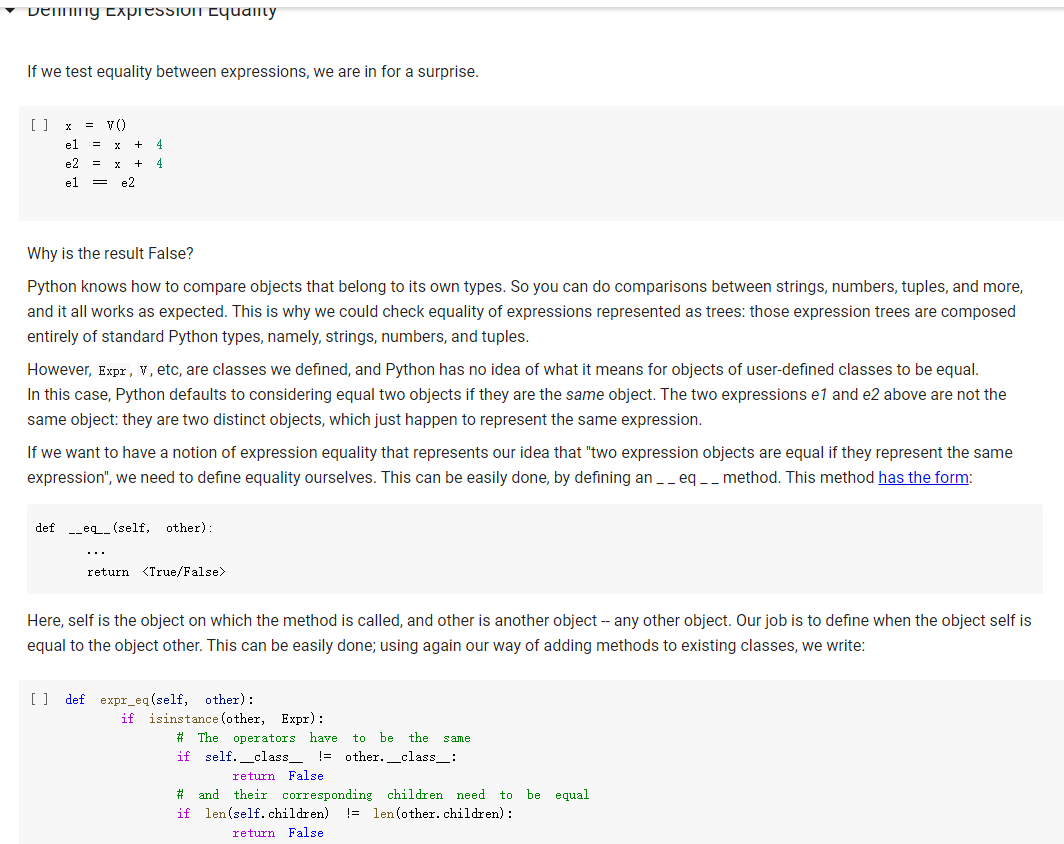
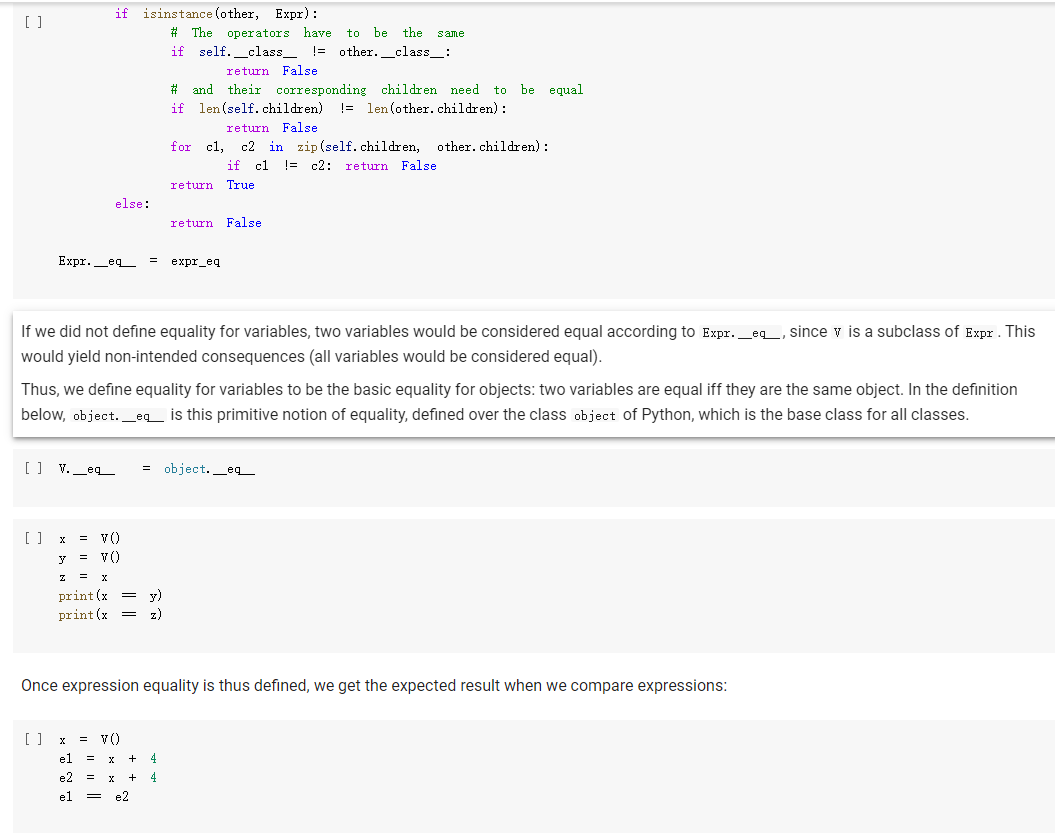
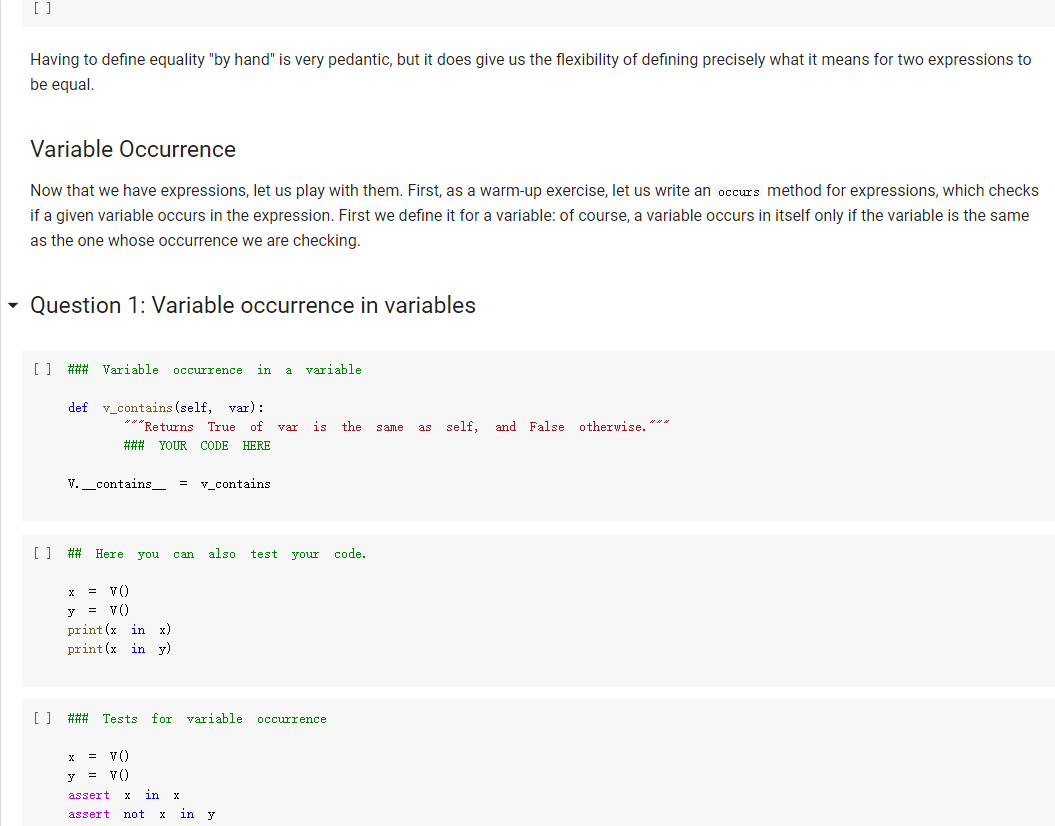

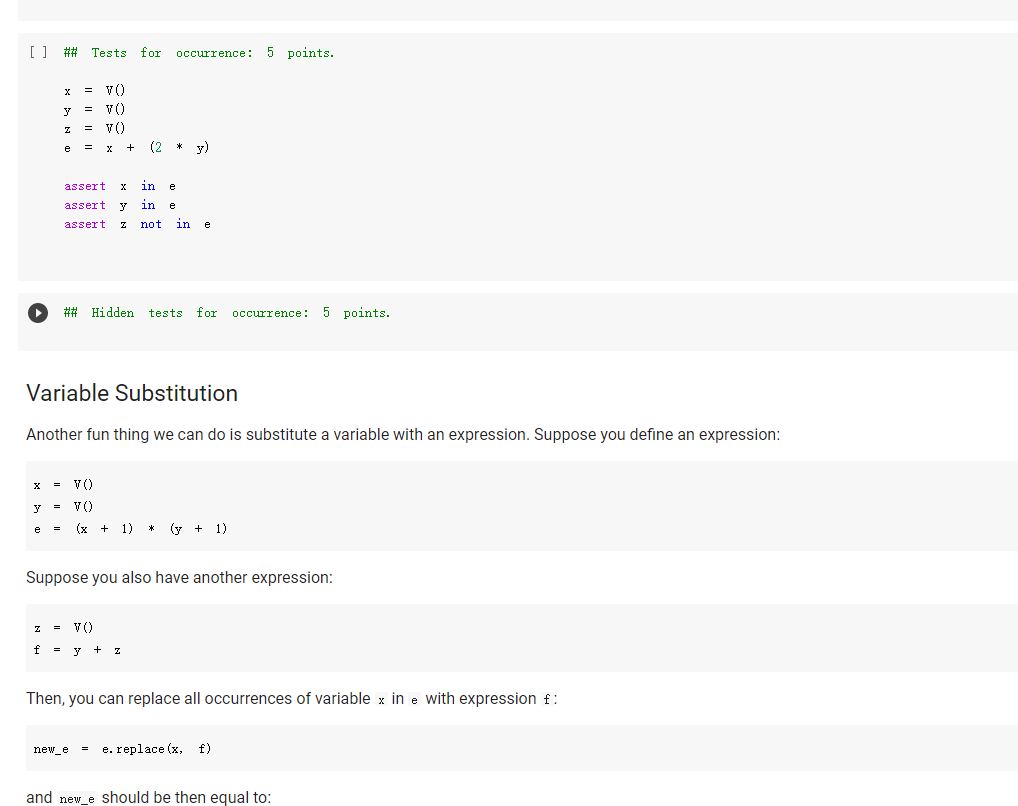
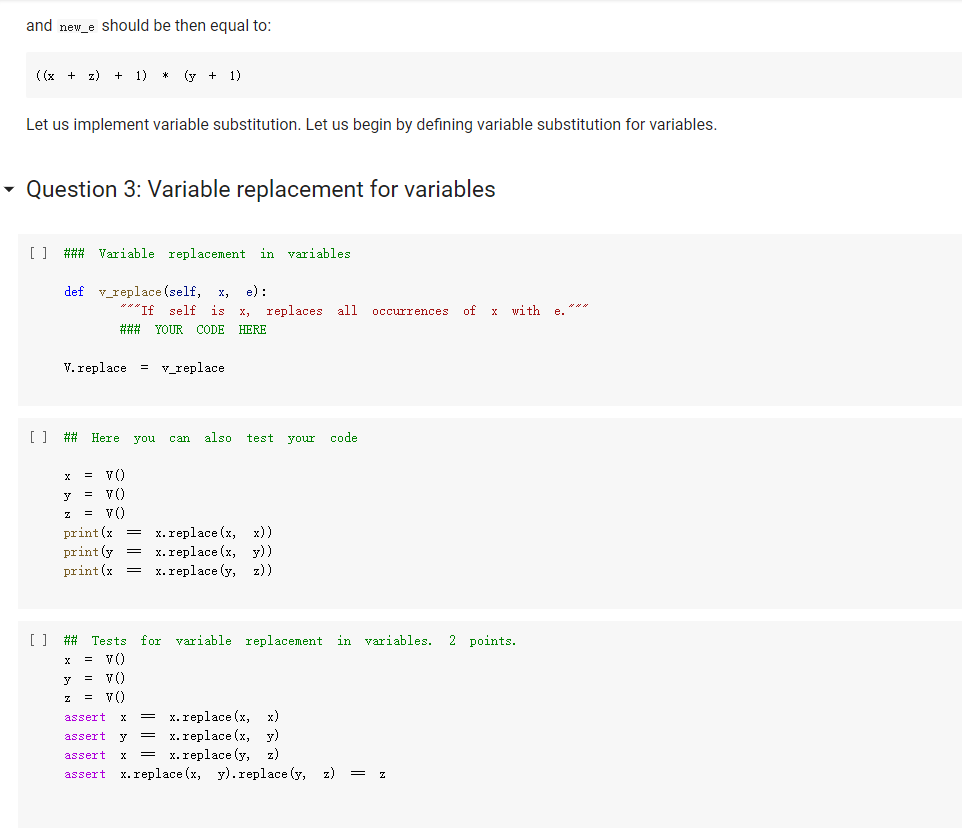
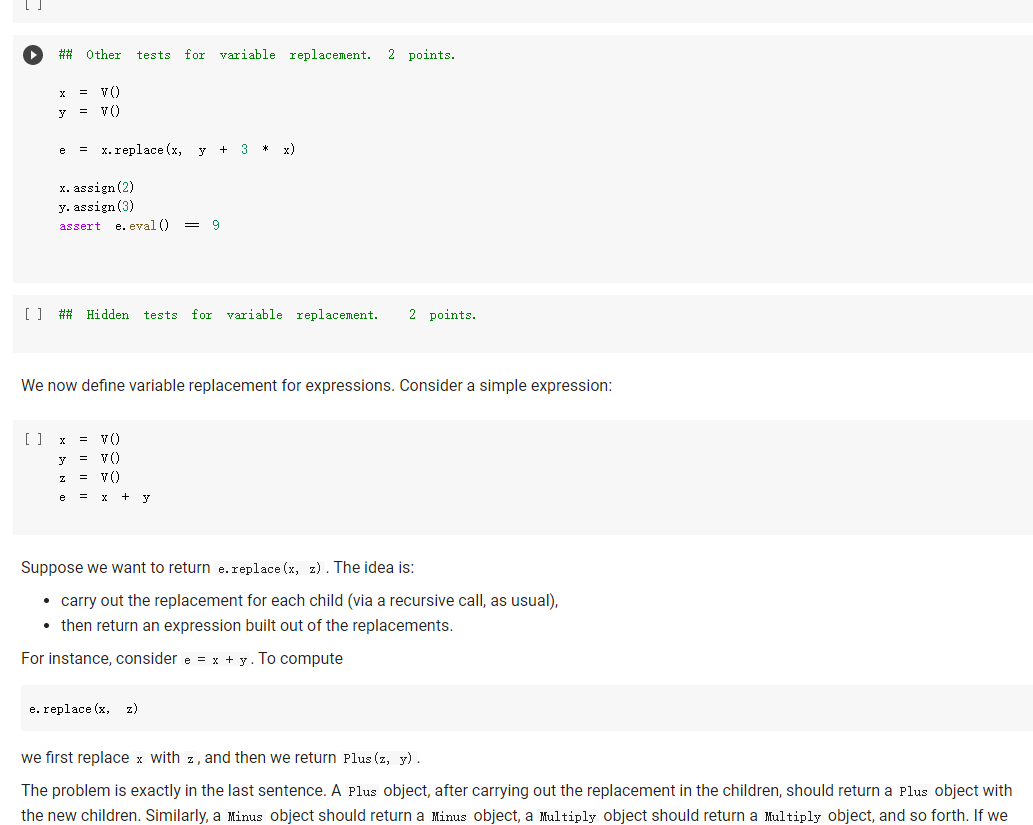
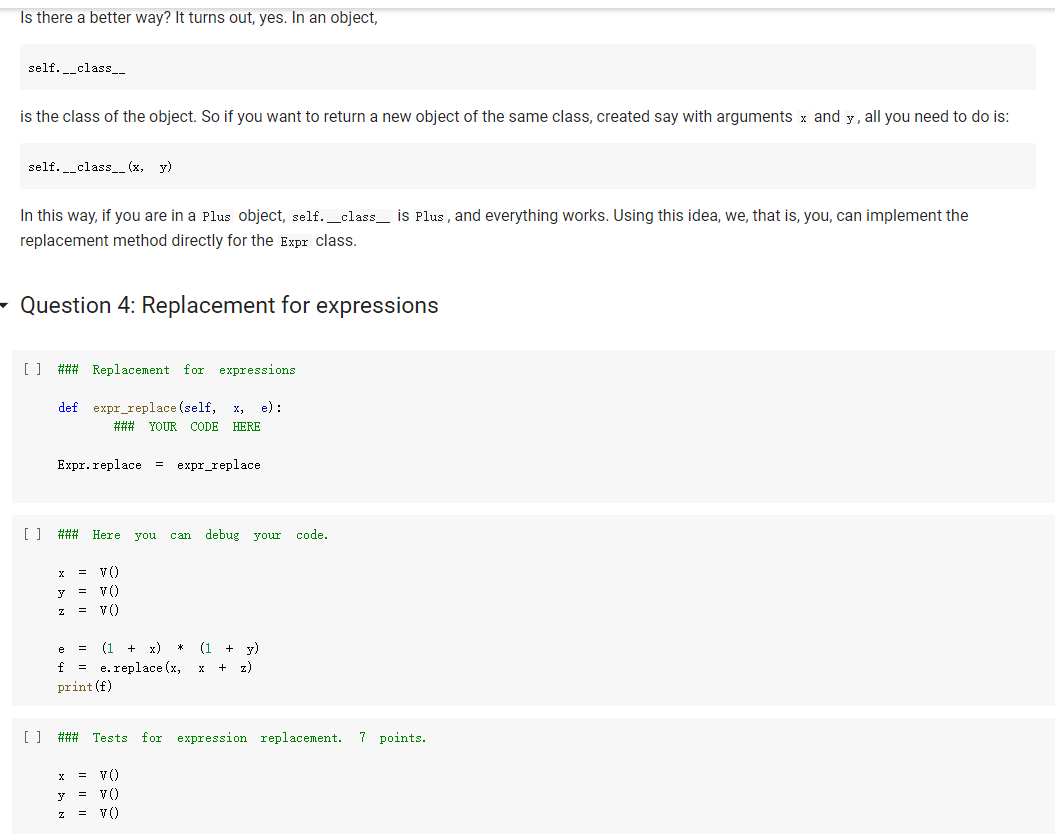
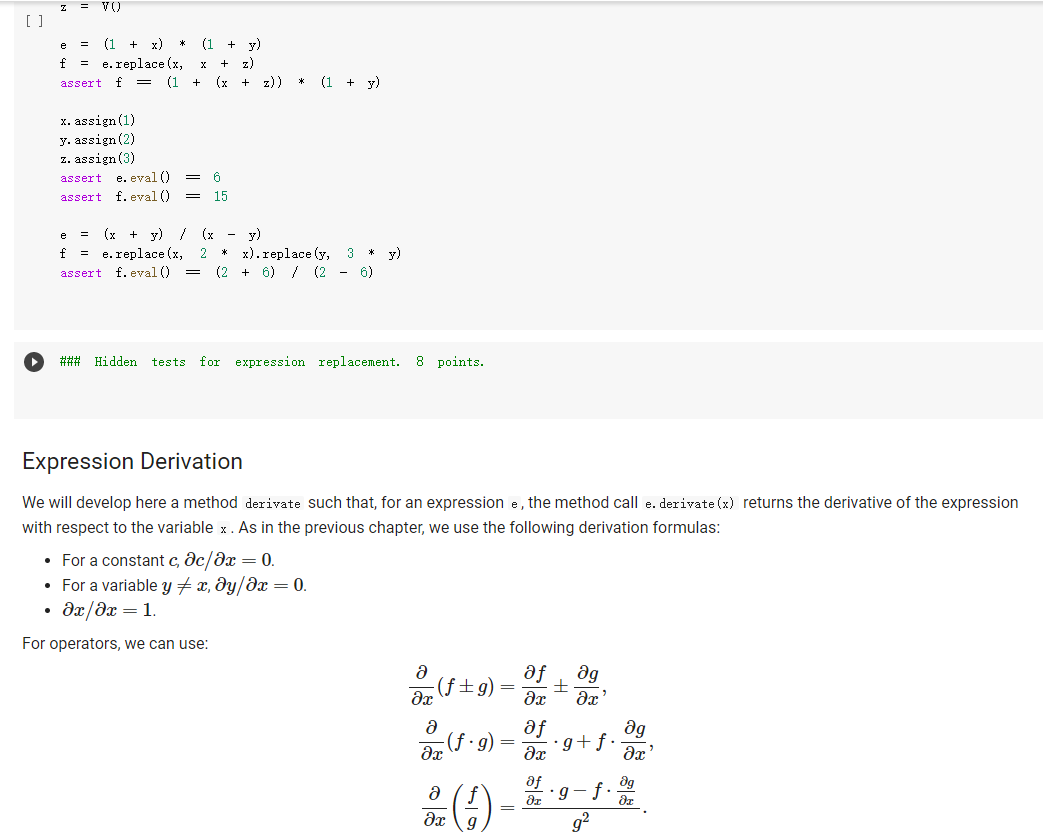
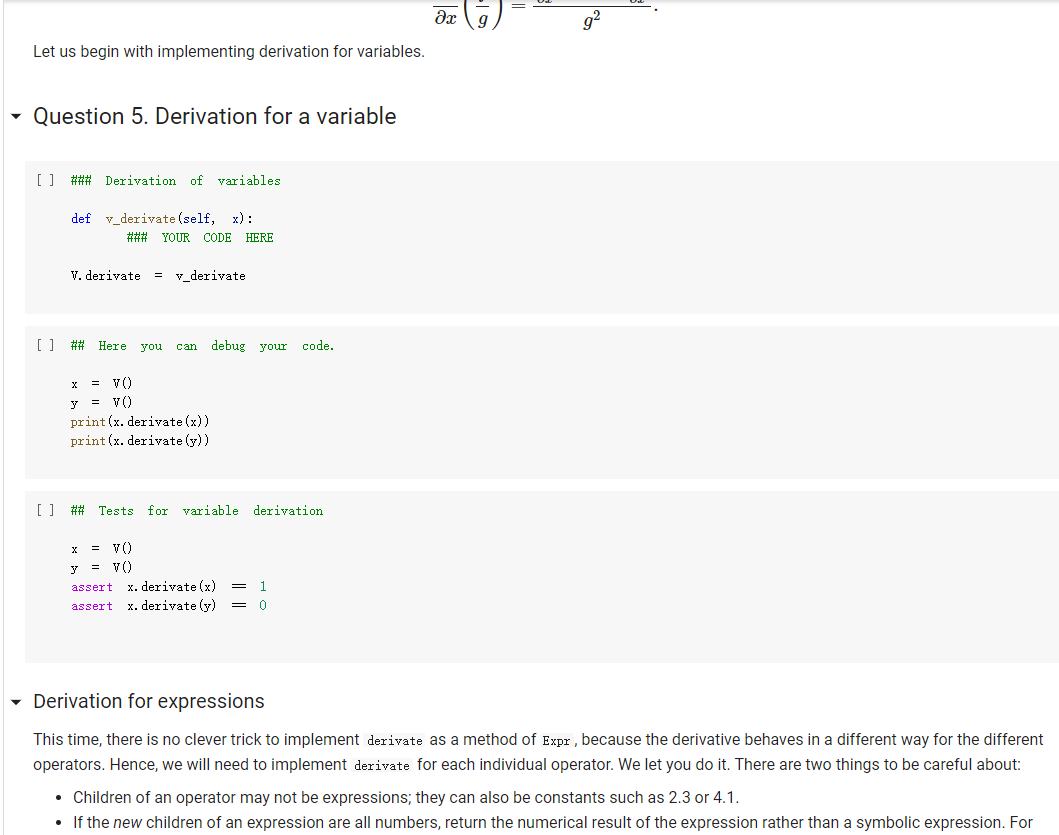
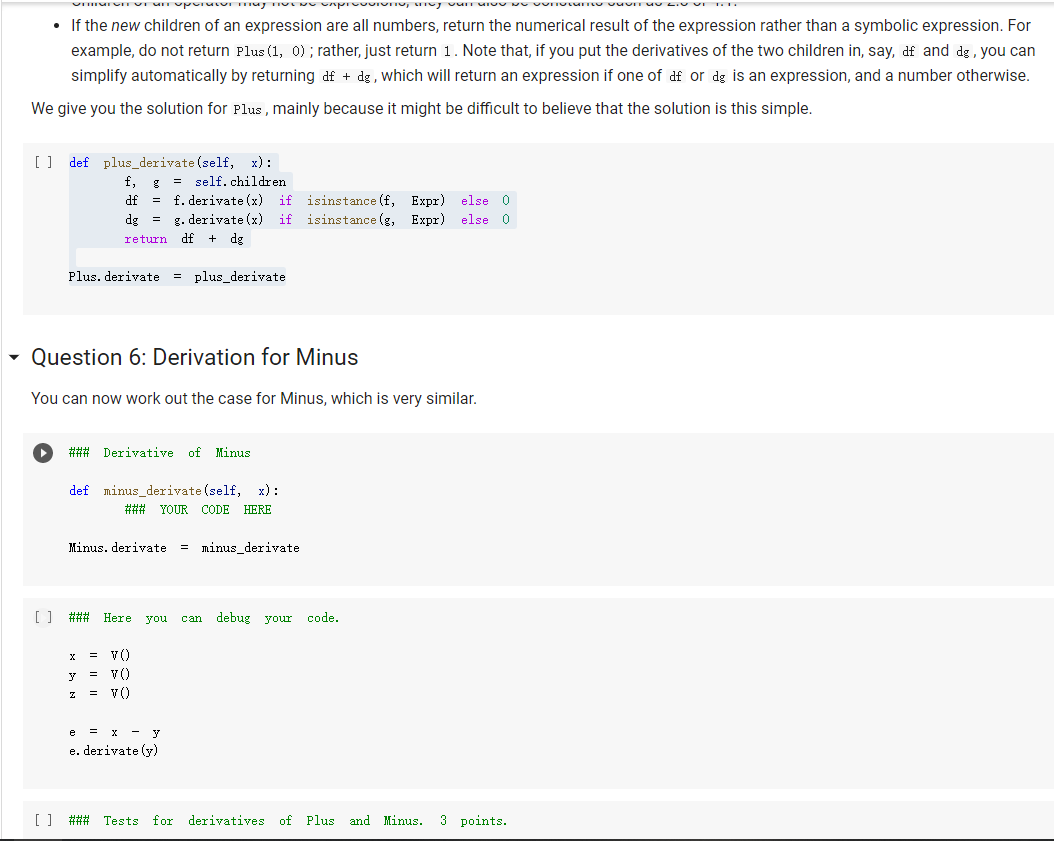
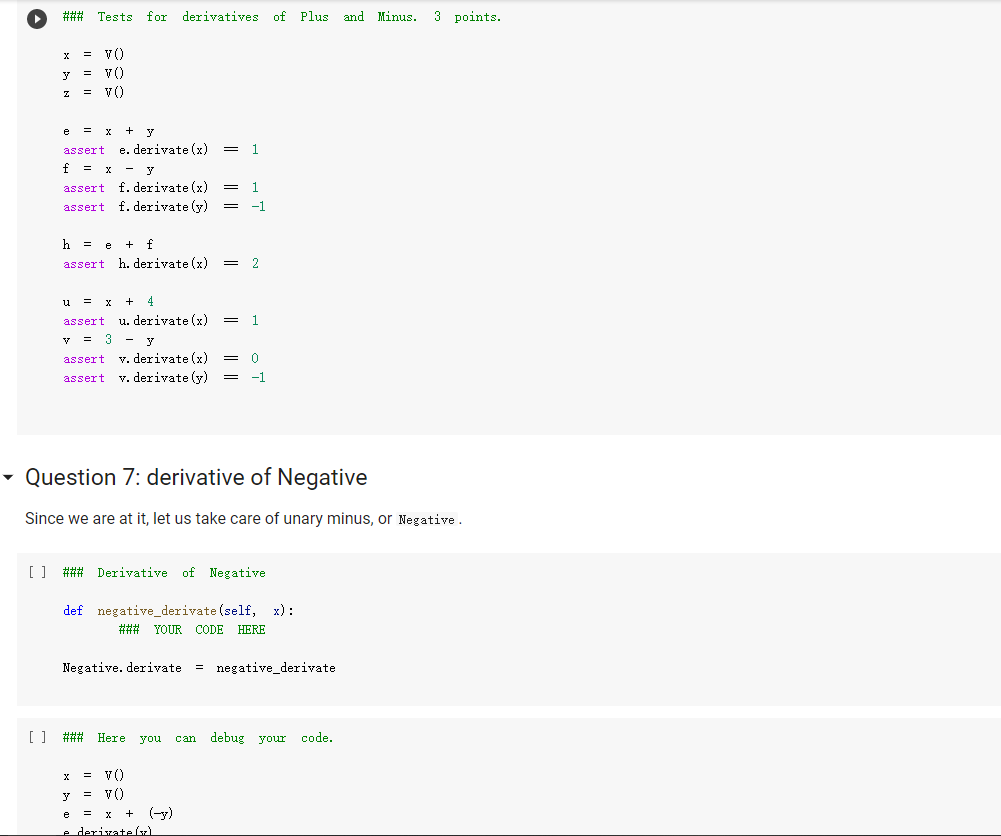

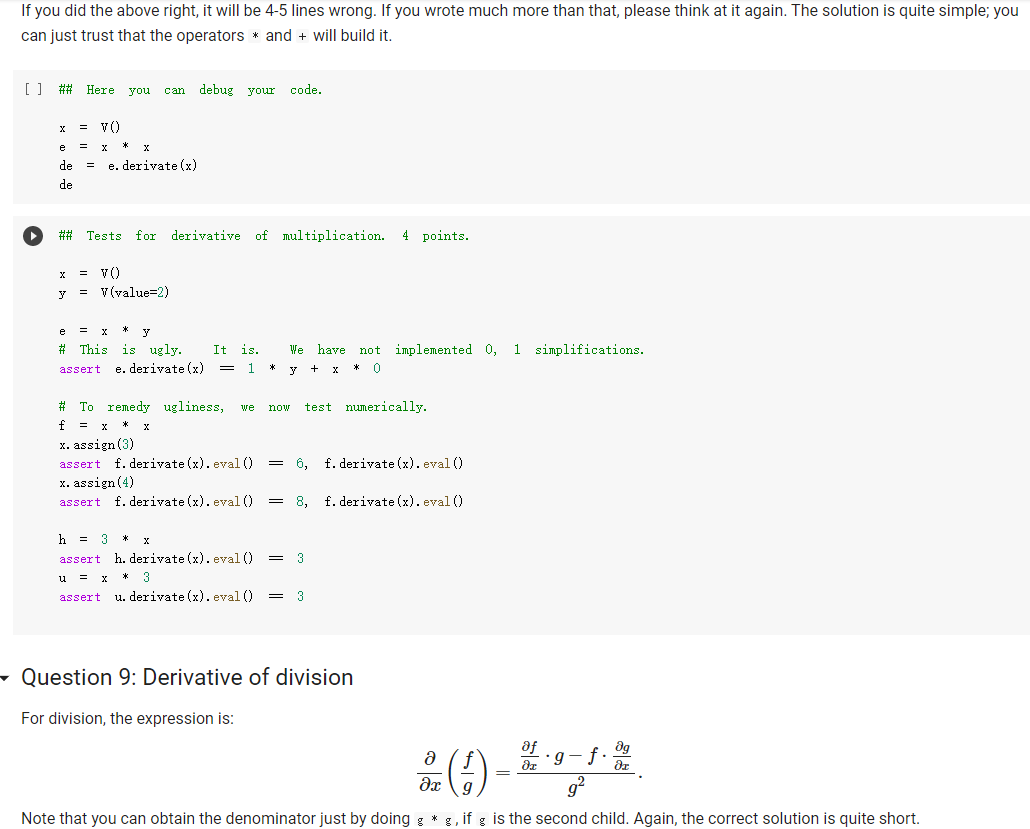

The Expr class The Expr class implements the various methods used to emulate numerical types, such as _add_, _sub_, and so forth. In this way, we can build an expression simply by writing x * 3 / 2 In the above, vo creates a variable (an object of class v), and assigns it to x. Then, x * 3 will also be an expression, composed of a multiplication node, with children the variable in x, and 3. The multiplication node is implemented via a subclass Multiply of Expr. To make this work, we will define the mul_ method of Expr so that it produces a Multiply object, with as children the two operands being multiplied. Similarly, x * 3 / 2 truediv will create an object of class Divide, with as left child the Multiply node for x * 3, and as right child, the number 2. Thus, the method of Expr will create a Divide node. Expressions can be evaluated. You can assign a value to variables either when you create them: x = V(value=2) e = x * 3 / 2 e. eval() which yields 3. Or you can assign a value to a variable later: e = x * 3 / 2 x. assign (3) which again yields 3. Benefits of class-based representation Compared with the representation of expressions seen in the previous chapter, this class-based representation offers several advantages. First, we can build expressions in a natural way as shown above, via the over-riding of the usual arithmetic operators. Second, if we introduce a new operator, all we need is provide the implementation of the new operator: We do not need to modify the shared code that traverses the tree, and add one more case to a long case-analysis. In other words, the code is far more modular. This may seem a small point, but if one were to extend the representation of expressions to involve tensors (matrices) and operations on tensors, as is done in the symbolic representation of expressions used in machine learning, the number of operators could easily grow to a hundred or more, making a modular approach the only reasonable one. Third, it becomes possible to attach methods to the expression objects, and as we will see in the next chapter, this can be very useful to implement machine learning frameworks. But later about that. - Defining an expression class We define an abstract class Expr, representing a generic expression. This generic class has as subclasses the classes that represent the various operators, such as Plus, Minus, Multiply, as well as the variable class v. Here is our basic implementation. [] class Expr (object): *** Abstract class representing expressions" name "expr* # Not used, but just to define it. def __init__(self, *args) : *** An object is created by passing to the constructor the children*** self.children = args self.value None # The value of the expression self.child_values = None # The values of the children: useful to have = def eval(self): = An object is created by passing to the constructor the children self.children args self.value None # The value of the expression self.child_values None # The values of the children: useful to have = = we def eval(self): Evaluates the expression. # First, evaluate the children. self.child_values [c. eval() if isinstance(c, Expr) else c for in self.children] # Then, evaluate the expression itself. self.value = self.op(*self.child_values) return self.value C we def op (self): ***This operator must be implemented in subclasses; it should compute self.value from self.values, thus implementing the operator at the expression node. raise NotImplementedError() def = name, repr_(self): Represents the expression in somewhat readable way. if len(self.children) 1: # Unary operators return "({}{})".format(self._class. self. children [0]) elif len(self.children) = 2: return "({}}{})". format self.children[0], self._class_.name, self.children[1] ) # Catch-all. return "{}({})". format (self._class__name__, ..join(repr (c) for C in self.children)) # Expression constructors def _add_(self, other): return Plus (self, other) def _radd_(self, other): return Plus (self, other) def _sub_(self, other) : return Minus (self, other) .join(repr (c) for C in self. children)) # Expression constructors def _add_(self, other): return Plus (self, other) def _radd__(self, other): return Plus (self, other) def _sub_(self, other): return Minus (self, other) def _rsub_(self, other): return Minus (other, self) def _mul_ (self, other): return Multiply(self, other) def_Imul_(self, other): return Multiply(other, self) def __truediv_(self, other): return Divide (self, other) def _rtruediv_(self, other): return Divide (other, self) def _neg__(self): return Negative (self) Variables are created specifying a name, and an initial value. If nothing is specified, variables have random initial values. You can assign a value to a variable using the assign method. The eval method of a variable simply returns its value. [] import random import string class V(Expr): ***Variable. *** def _init__(self, value=None): import random import string class V(Expr): ***Variable. def __init__(self, value=None): super(). _init_o self.children = [] self.value = random. gauss (0, 1) if value is None else value self.name ''. join random. choices (string. ascii_letters + string. digits, k=3)) = def eval(self): return self.value def assign(self, value): self.value = value def __repr__(self): return "Y(I, value={})".format(self.name, self.value) Here are the constructors for the other operators; for them, we just need to provide an implementation for op, since all the rest is inherited from Expr. We actually also define a name, as a class attribute, that we use in the representation method. = [] class Plus (Expr): name " + def op (self, return x, y): + y class Minus (Expr): name def op (self, x, y): return x - y class Multiply(Expr): name def op (self, x, y): return x * y class Divide (Expr): [] class Divide (Expr): name = "/" def op (self, return x, y): class Negative (Expr): name def op (self, x): return -X We can build and evaluate expressions quite simply. e = V(2) + 3 print(e) print(e. eval() * (2 + V(1)) [ ] e = (VO) + V(2)) print(e) print(e. eval()) If we want to be able to assign values to variables, or refer to them in our code later, we need to assign our variable objects to Python variables: [] x = Y() y = vO) e = x + y print(e. eval()) # This uses the initial random values. x. assign (2) y. assign (3) print(e. eval() Defining Expression Equality Denny expression quality If we test equality between expressions, we are in for a surprise. 4 [] x el e2 el = VO) = X + = x = e2 + 4 Why is the result False? Python knows how to compare objects that belong to its own types. So you can do comparisons between strings, numbers, tuples, and more, and it all works as expected. This is why we could check equality of expressions represented as trees: those expression trees are composed entirely of standard Python types, namely, strings, numbers, and tuples. However, Expr, V, etc, are classes we defined, and Python has no idea of what it means for objects of user-defined classes to be equal. In this case, Python defaults to considering equal two objects if they are the same object. The two expressions e1 and e2 above are not the same object: they are two distinct objects, which just happen to represent the same expression. If we want to have a notion of expression equality that represents our idea that "two expression objects are equal if they represent the same expression", we need to define equality ourselves. This can be easily done, by defining an--eq -- method. This method has the form: def --ec_(self, other): return Here, self is the object on which the method is called, and other is another object -- any other object. Our job is to define when the object self is equal to the object other. This can be easily done; using again our way of adding methods to existing classes, we write: same [] def expr_eq(self, other): if isinstance (other, Expr): # The operators have to be the if self._class_ != other. _class_: return false # and their corresponding children need to be equal if len(self.children) != len(other children): return false [] if isinstance (other, Expr): # The operators have to to be the same if self._class__ != other._class_: return false # and their corresponding children need to be equal if len(self.children) != len(other children): return false for c1, c2 in zip (self.children, other. children): if c1 != c2: return false return True else: return false Expr. _eq_ . = expr_ea If we did not define equality for variables, two variables would be considered equal according to Expr. _eq_, since v is a subclass of Expr. This would yield non-intended consequences (all variables would be considered equal). Thus, we define equality for variables to be the basic equality for objects: two variables are equal iff they are the same object. In the definition below, object. _eq_ is this primitive notion of equality, defined over the class object of Python, which is the base class for all classes. [] V. _eq_ = object. _eq_ [ ] = VO y = VO = x print(x = y) print (x Z Once expression equality is thus defined, we get the expected result when we compare expressions: [] = VO + el 4 4 e2 X + el = e2 [] Having to define equality "by hand" is very pedantic, but it does give us the flexibility of defining precisely what it means for two expressions to be equal. Variable Occurrence Now that we have expressions, let us play with them. First, as a warm-up exercise, let us write an occurs method for expressions, which checks if a given variable occurs in the expression. First we define it for a variable: of course, a variable occurs in itself only if the variable is the same as the one whose occurrence we are checking. Question 1: Variable occurrence in variables [] ### Variable occurrence in a variable def v_contains (self, var): Returns True of ### YOUR CODE HERE *** var is the same as self, and False otherwise. *** V. _contains_ = v_contains [] ## Here Here you can also test your code. = vO) y = v) print(x in x) print(x in y) [] ### Tests for variable occurrence = vO) y = V() assert x in X assert not X in y [] ### Tests for variable occurrence = VO = v) y assert in assert not x in Y Z = X assert in Z Question 2: Occurrence of a variable in an expression Once we define occurrence of a variable in a variable, we can define occurrence in a variable in a general expression. Of course, a variable appears in an expression if it appears in some of its children. [ ] ### Occurrence of a variable in an expression def expr_contains (self, var): ### YOUR CODE HERE Expr. _contains_ = expr_contains [] ## Here you can also test your code. = VO) y = V() Z = VO e = x + (2 * y) print(x in e) printly in e) print(z in e) [] ## Tests for occurrence: 5 points. x = VO [ ] ## Tests for occurrence: 5 points. X = v) y = Y() Z = VO e = X + (2 assert in assert y in Z not assert in e ## Hidden tests for occurrence: 5 points. Variable Substitution Another fun thing we can do is substitute a variable with an expression. Suppose you define an expression: x = V() (x + 1) * (y + 1) Suppose you also have another expression: f = y + Z Then, you can replace all occurrences of variable x in e with expression f: new_e = e.replace(x, f) and new_e should be then equal to: and new_e should be then equal to: ((x + Z) + 1) * (y + 1) Let us implement variable substitution. Let us begin by defining variable substitution for variables. Question 3: Variable replacement for variables [] ### Variable replacement in variables def v_replace(self, x, e): ***If self is x, replaces all ### YOUR CODE HERE occurrences of X with e. *** V.replace = v_replace [] ## Here you can also test your code = Y() y = VO = VO print(x = print (y print(x x.replace(x,x)) x.replace(x, y)) x.replace(y, z)) [] Z ## Tests for variable replacement in variables. 2 points. = V0) = VO = Y() assert X.replace(x, x) assert X.replace(x, y) assert x.replace(y, z) assert X.replace(x, y).replace(y, z) = z ## Other tests for variable replacement. 2 points. = Y() = VO e = x.replace(x, y + 3 * x) x. assign (2) y. assign (3) assert e. eval() = 9 [] ## Hidden tests for variable replacement. 2 points. We now define variable replacement for expressions. Consider a simple expression: [] x = V) VO e = x + y Suppose we want to return e.replace(x, z). The idea is: carry out the replacement for each child (via a recursive call, as usual), then return an expression built out of the replacements. For instance, consider e = x + y. To compute e. replace (x, z) we first replace x with z, and then we return Plus (z, y). The problem is exactly in the last sentence. A Plus object, after carrying out the replacement in the children, should return a Plus object with the new children. Similarly, a Minus object should return a Minus object, a Multiply object should return a Multiply object, and so forth. If we Is there a better way? It turns out, yes. In an object, self.__class_- is the class of the object. So if you want to return a new object of the same class, created say with arguments x and y, all you need to do is: self.__class__(x, y) In this way, if you are in a plus object, self._class_ is Plus, and everything works. Using this idea, we, that is, you, can implement the replacement method directly for the Expr class. - Question 4: Replacement for expressions [ ] ### Replacement for expressions def expr_replace(self, x, e): ### YOUR CODE HERE Expr. replace = expr_replace [] ### Here you can debug your code. X y = vO) = v) = VO * (1 + x) (1 + y) f = e.replace(x, x + z) print (f) [] ### Tests for expression replacement. 7 points. = Y() = VO = vO) Z = VO [] (1 + x) * (1 + y) f = e.replace(x, x + z) assert f = (1 + (x + z)) * (1 + y) x. assign (1) y. assign (2) z. assign (3) assert e. eval() assert f. eval() = 6 = 15 e = (x + y) / (x - y) = e.replace(x, 2 * x).replace(y, 3 * y) assert f.eval() = (2 + 6) 1 (2 - 6) f ### Hidden tests for expression replacement. 8 points. Expression Derivation We will develop here a method derivate such that, for an expression e, the method call e. derivate (x) returns the derivative of the expression with respect to the variable x. As in the previous chapter, we use the following derivation formulas: For a constant c, ac/ax = 0. For a variable y + x, dy/ax=0. z/x = 1 For operators, we can use: a af (f+g) + ar ax ar a af (f:9) ar ax ac ag ag 9+f a af 9-f Og = ac 9 92 ar Let us begin with implementing derivation for variables. Question 5. Derivation for a variable [ ] ### Derivation of variables def v_derivate (self, x): ### YOUR CODE HERE V. derivate = v_derivate [] ## Here you can debug your code. = VO y = VO print(x. derivate (x)) print(x. derivate (y)) [] ## Tests for variable derivation y = VO assert x. derivate (x) assert x. derivate (y) = 1 = 0 - Derivation for expressions This time, there is no clever trick to implement derivate as a method of Expr, because the derivative behaves in a different way for the different operators. Hence, we will need to implement derivate for each individual operator. We let you do it. There are two things to be careful about: Children of an operator may not be expressions; they can also be constants such as 2.3 or 4.1. If the new children of an expression are all numbers, return the numerical result of the expression rather than a symbolic expression. For HUTCHOU poruLVI may norwerpico, Van If the new children of an expression are all numbers, return the numerical result of the expression rather than a symbolic expression. For example, do not return Plus (1, 0); rather, just return 1. Note that, if you put the derivatives of the two children in, say, df and dg , you can simplify automatically by returning df + dg, which will return an expression if one of df or dg is an expression, and a number otherwise. We give you the solution for Plus , mainly because it might be difficult to believe that the solution is this simple. [] def plus_derivate (self, x): f, self.children df = f. derivate (x) if isinstance(f, Expr) else 0 dg = g. derivate (x) if isinstance(g, Expr) else 0 return df + dg Plus. derivate = plus_derivate Question 6: Derivation for Minus You can now work out the case for Minus, which is very similar. ### Derivative of Minus def minus_derivate (self, x): ### YOUR CODE HERE Minus. derivate = minus_derivate [] ### Here you can debug your code. = VO) Y = V) z = VO) e. derivate (y) [] ### Tests for derivatives of Plus and Minus. 3 points. ### Tests Tests for derivatives of Plus and Minus. 3 points. y = V) = vO) = VO) Z e = 1 = x + y + assert e. derivate (x) f = x - y assert f. derivate (x) assert f. derivate (y) 1 -1 h = e + f assert h. derivate (x) = 2 = 1 u = X x + 4 assert u. derivate (x) V = 3 - y assert v. derivate (x) assert v. derivate (y) 0 -1 Question 7: derivative of Negative Since we are at it, let us take care of unary minus, or Negative. [] ### Derivative of Negative def negative_derivate (self, x): ### YOUR CODE HERE Negative. derivate = negative_derivate [] ### ### Here you can debug your code. = vO) = VO y e e derivate [] ### Here you can debug your code. y = v) e = x + (-y) e. derivate (y) [] ### Tests for negative. 4 points. = y = VO E assert e. derivate (x) e. derivate (y) -1 0 assert = 9+f. Now for multiplication and divisions. Be careful to use the formulas exactly as given, otherwise the result may not match. E.g. use a af ag (f.g) ar og and not, for instance, & (fg) =9 +f. ar (note the swap of the factors in the first term). We would like you to return simplified expressions. You can again use the trick that, if you have two expressions df and g or similar), then df * g will be an expression if one of df and g are expressions, and a number if both df and g are numbers. Question 8: Derivation of multiplication [] ### Derivative of multiplication. def multiply_derivate (self, x): ### YOUR CODE HERE Multiply. derivate = multiply derivate If you did the above right, it will be 4-5 lines wrong. If you wrote much more than that, please think at it again. The solution is quite simple; you If you did the above right, it will be 4-5 lines wrong. If you wrote much more than that, please think at it again. The solution is quite simple; you can just trust that the operators * and + will build it. [] ## Here you can debug your code. = V) e = * x de e. derivate (x) de = ## Tests for derivative of multiplication. 4 points. x = VO = V(value=2) y e X Y # This is ugly. assert e. derivate (x) 1 simplifications. It is. 1 We have not implemented 0, x * 0 * + we now test numerically. # To remedy ugliness, f = X * x. assign (3) assert f. derivate (x). eval() x. assign (4) assert f. derivate (x). eval() = 6, f. derivate(x). eval() = 8, f. derivate (x). eval() 3 h = 3 * * assert h. derivate (x). eval() u * 3 assert u. derivate (x). eval() = 3 Question 9: Derivative of division For division, the expression is: af a z ar 9 g Note that you can obtain the denominator just by doing g *g, if g is the second child. Again, the correct solution is quite short. For division, the expression is: af . 9 a ar (1) 92 Note that you can obtain the denominator just by doing g* g, if g is the second child. Again, the correct solution is quite short. [ ] ### Derivative of division def divide_derivate (self, x): ### YOUR CODE HERE Divide. derivate = divide_derivate Here you can debug your code. x = vO) y = VO print("x", print("y:", y) e = x/y e. derivate (y) [] ### Tests for derivative of division. 4 points. X e = YO) y = V0) = X / 2 f = e. derivate (x) x. assign (3) assert f. eval() = 1/2 g = 1 x assert g. derivate (x). eval() assert g. derivate (y). eval() = - 1 / 9 0 = [] ## Miscellaneous tests. 3 points. X = V(value=2) V(value=3) f df (x + 1) (y + 1) / (x - 1) * ( - 1) = f. derivate (x) assert df. eval() = -16 x. assign (0.5) y. assign (0.5) assert df. eval() = 6 ## Miscellaneous tests. 3 points. = V(value=0) f = (3 + 2 * x + 4) / (5 * x * x 7 * x + 12) df = f. derivate (x) assert abs (df. eval() - 0.3611) Here, self is the object on which the method is called, and other is another object -- any other object. Our job is to define when the object self is equal to the object other. This can be easily done; using again our way of adding methods to existing classes, we write: same [] def expr_eq(self, other): if isinstance (other, Expr): # The operators have to be the if self._class_ != other. _class_: return false # and their corresponding children need to be equal if len(self.children) != len(other children): return false [] if isinstance (other, Expr): # The operators have to to be the same if self._class__ != other._class_: return false # and their corresponding children need to be equal if len(self.children) != len(other children): return false for c1, c2 in zip (self.children, other. children): if c1 != c2: return false return True else: return false Expr. _eq_ . = expr_ea If we did not define equality for variables, two variables would be considered equal according to Expr. _eq_, since v is a subclass of Expr. This would yield non-intended consequences (all variables would be considered equal). Thus, we define equality for variables to be the basic equality for objects: two variables are equal iff they are the same object. In the definition below, object. _eq_ is this primitive notion of equality, defined over the class object of Python, which is the base class for all classes. [] V. _eq_ = object. _eq_ [ ] = VO y = VO = x print(x = y) print (x Z Once expression equality is thus defined, we get the expected result when we compare expressions: [] = VO + el 4 4 e2 X + el = e2 [] Having to define equality "by hand" is very pedantic, but it does give us the flexibility of defining precisely what it means for two expressions to be equal. Variable Occurrence Now that we have expressions, let us play with them. First, as a warm-up exercise, let us write an occurs method for expressions, which checks if a given variable occurs in the expression. First we define it for a variable: of course, a variable occurs in itself only if the variable is the same as the one whose occurrence we are checking. Question 1: Variable occurrence in variables [] ### Variable occurrence in a variable def v_contains (self, var): Returns True of ### YOUR CODE HERE *** var is the same as self, and False otherwise. *** V. _contains_ = v_contains [] ## Here Here you can also test your code. = vO) y = v) print(x in x) print(x in y) [] ### Tests for variable occurrence = vO) y = V() assert x in X assert not X in y [] ### Tests for variable occurrence = VO = v) y assert in assert not x in Y Z = X assert in Z Question 2: Occurrence of a variable in an expression Once we define occurrence of a variable in a variable, we can define occurrence in a variable in a general expression. Of course, a variable appears in an expression if it appears in some of its children. [ ] ### Occurrence of a variable in an expression def expr_contains (self, var): ### YOUR CODE HERE Expr. _contains_ = expr_contains [] ## Here you can also test your code. = VO) y = V() Z = VO e = x + (2 * y) print(x in e) printly in e) print(z in e) [] ## Tests for occurrence: 5 points. x = VO [ ] ## Tests for occurrence: 5 points. X = v) y = Y() Z = VO e = X + (2 assert in assert y in Z not assert in e ## Hidden tests for occurrence: 5 points. Variable Substitution Another fun thing we can do is substitute a variable with an expression. Suppose you define an expression: x = V() (x + 1) * (y + 1) Suppose you also have another expression: f = y + Z Then, you can replace all occurrences of variable x in e with expression f: new_e = e.replace(x, f) and new_e should be then equal to: and new_e should be then equal to: ((x + Z) + 1) * (y + 1) Let us implement variable substitution. Let us begin by defining variable substitution for variables. Question 3: Variable replacement for variables [] ### Variable replacement in variables def v_replace(self, x, e): ***If self is x, replaces all ### YOUR CODE HERE occurrences of X with e. *** V.replace = v_replace [] ## Here you can also test your code = Y() y = VO = VO print(x = print (y print(x x.replace(x,x)) x.replace(x, y)) x.replace(y, z)) [] Z ## Tests for variable replacement in variables. 2 points. = V0) = VO = Y() assert X.replace(x, x) assert X.replace(x, y) assert x.replace(y, z) assert X.replace(x, y).replace(y, z) = z ## Other tests for variable replacement. 2 points. = Y() = VO e = x.replace(x, y + 3 * x) x. assign (2) y. assign (3) assert e. eval() = 9 [] ## Hidden tests for variable replacement. 2 points. We now define variable replacement for expressions. Consider a simple expression: [] x = V) VO e = x + y Suppose we want to return e.replace(x, z). The idea is: carry out the replacement for each child (via a recursive call, as usual), then return an expression built out of the replacements. For instance, consider e = x + y. To compute e. replace (x, z) we first replace x with z, and then we return Plus (z, y). The problem is exactly in the last sentence. A Plus object, after carrying out the replacement in the children, should return a Plus object with the new children. Similarly, a Minus object should return a Minus object, a Multiply object should return a Multiply object, and so forth. If we Is there a better way? It turns out, yes. In an object, self.__class_- is the class of the object. So if you want to return a new object of the same class, created say with arguments x and y, all you need to do is: self.__class__(x, y) In this way, if you are in a plus object, self._class_ is Plus, and everything works. Using this idea, we, that is, you, can implement the replacement method directly for the Expr class. - Question 4: Replacement for expressions [ ] ### Replacement for expressions def expr_replace(self, x, e): ### YOUR CODE HERE Expr. replace = expr_replace [] ### Here you can debug your code. X y = vO) = v) = VO * (1 + x) (1 + y) f = e.replace(x, x + z) print (f) [] ### Tests for expression replacement. 7 points. = Y() = VO = vO) Z = VO [] (1 + x) * (1 + y) f = e.replace(x, x + z) assert f = (1 + (x + z)) * (1 + y) x. assign (1) y. assign (2) z. assign (3) assert e. eval() assert f. eval() = 6 = 15 e = (x + y) / (x - y) = e.replace(x, 2 * x).replace(y, 3 * y) assert f.eval() = (2 + 6) 1 (2 - 6) f ### Hidden tests for expression replacement. 8 points. Expression Derivation We will develop here a method derivate such that, for an expression e, the method call e. derivate (x) returns the derivative of the expression with respect to the variable x. As in the previous chapter, we use the following derivation formulas: For a constant c, ac/ax = 0. For a variable y + x, dy/ax=0. z/x = 1 For operators, we can use: a af (f+g) + ar ax ar a af (f:9) ar ax ac ag ag 9+f a af 9-f Og = ac 9 92 ar Let us begin with implementing derivation for variables. Question 5. Derivation for a variable [ ] ### Derivation of variables def v_derivate (self, x): ### YOUR CODE HERE V. derivate = v_derivate [] ## Here you can debug your code. = VO y = VO print(x. derivate (x)) print(x. derivate (y)) [] ## Tests for variable derivation y = VO assert x. derivate (x) assert x. derivate (y) = 1 = 0 - Derivation for expressions This time, there is no clever trick to implement derivate as a method of Expr, because the derivative behaves in a different way for the different operators. Hence, we will need to implement derivate for each individual operator. We let you do it. There are two things to be careful about: Children of an operator may not be expressions; they can also be constants such as 2.3 or 4.1. If the new children of an expression are all numbers, return the numerical result of the expression rather than a symbolic expression. For HUTCHOU poruLVI may norwerpico, Van If the new children of an expression are all numbers, return the numerical result of the expression rather than a symbolic expression. For example, do not return Plus (1, 0); rather, just return 1. Note that, if you put the derivatives of the two children in, say, df and dg , you can simplify automatically by returning df + dg, which will return an expression if one of df or dg is an expression, and a number otherwise. We give you the solution for Plus , mainly because it might be difficult to believe that the solution is this simple. [] def plus_derivate (self, x): f, self.children df = f. derivate (x) if isinstance(f, Expr) else 0 dg = g. derivate (x) if isinstance(g, Expr) else 0 return df + dg Plus. derivate = plus_derivate Question 6: Derivation for Minus You can now work out the case for Minus, which is very similar. ### Derivative of Minus def minus_derivate (self, x): ### YOUR CODE HERE Minus. derivate = minus_derivate [] ### Here you can debug your code. = VO) Y = V) z = VO) e. derivate (y) [] ### Tests for derivatives of Plus and Minus. 3 points. ### Tests Tests for derivatives of Plus and Minus. 3 points. y = V) = vO) = VO) Z e = 1 = x + y + assert e. derivate (x) f = x - y assert f. derivate (x) assert f. derivate (y) 1 -1 h = e + f assert h. derivate (x) = 2 = 1 u = X x + 4 assert u. derivate (x) V = 3 - y assert v. derivate (x) assert v. derivate (y) 0 -1 Question 7: derivative of Negative Since we are at it, let us take care of unary minus, or Negative. [] ### Derivative of Negative def negative_derivate (self, x): ### YOUR CODE HERE Negative. derivate = negative_derivate [] ### ### Here you can debug your code. = vO) = VO y e e derivate [] ### Here you can debug your code. y = v) e = x + (-y) e. derivate (y) [] ### Tests for negative. 4 points. = y = VO E assert e. derivate (x) e. derivate (y) -1 0 assert = 9+f. Now for multiplication and divisions. Be careful to use the formulas exactly as given, otherwise the result may not match. E.g. use a af ag (f.g) ar og and not, for instance, & (fg) =9 +f. ar (note the swap of the factors in the first term). We would like you to return simplified expressions. You can again use the trick that, if you have two expressions df and g or similar), then df * g will be an expression if one of df and g are expressions, and a number if both df and g are numbers. Question 8: Derivation of multiplication [] ### Derivative of multiplication. def multiply_derivate (self, x): ### YOUR CODE HERE Multiply. derivate = multiply derivate If you did the above right, it will be 4-5 lines wrong. If you wrote much more than that, please think at it again. The solution is quite simple; you If you did the above right, it will be 4-5 lines wrong. If you wrote much more than that, please think at it again. The solution is quite simple; you can just trust that the operators * and + will build it. [] ## Here you can debug your code. = V) e = * x de e. derivate (x) de = ## Tests for derivative of multiplication. 4 points. x = VO = V(value=2) y e X Y # This is ugly. assert e. derivate (x) 1 simplifications. It is. 1 We have not implemented 0, x * 0 * + we now test numerically. # To remedy ugliness, f = X * x. assign (3) assert f. derivate (x). eval() x. assign (4) assert f. derivate (x). eval() = 6, f. derivate(x). eval() = 8, f. derivate (x). eval() 3 h = 3 * * assert h. derivate (x). eval() u * 3 assert u. derivate (x). eval() = 3 Question 9: Derivative of division For division, the expression is: af a z ar 9 g Note that you can obtain the denominator just by doing g *g, if g is the second child. Again, the correct solution is quite short. For division, the expression is: af . 9 a ar (1) 92 Note that you can obtain the denominator just by doing g* g, if g is the second child. Again, the correct solution is quite short. [ ] ### Derivative of division def divide_derivate (self, x): ### YOUR CODE HERE Divide. derivate = divide_derivate Here you can debug your code. x = vO) y = VO print("x", print("y:", y) e = x/y e. derivate (y) [] ### Tests for derivative of division. 4 points. X e = YO) y = V0) = X / 2 f = e. derivate (x) x. assign (3) assert f. eval() = 1/2 g = 1 x assert g. derivate (x). eval() assert g. derivate (y). eval() = - 1 / 9 0 = [] ## Miscellaneous tests. 3 points. X = V(value=2) V(value=3) f df (x + 1) (y + 1) / (x - 1) * ( - 1) = f. derivate (x) assert df. eval() = -16 x. assign (0.5) y. assign (0.5) assert df. eval() = 6 ## Miscellaneous tests. 3 points. = V(value=0) f = (3 + 2 * x + 4) / (5 * x * x 7 * x + 12) df = f. derivate (x) assert abs (df. eval() - 0.3611)

























