

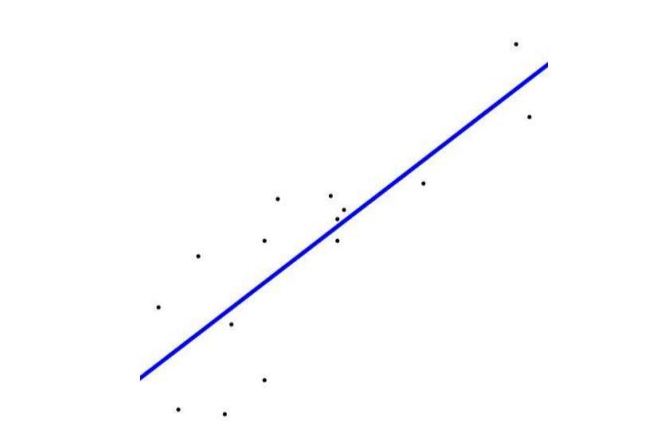


The file crickets.txt (available on eCampus) contains data for 15 crickets (use a final variable!). The first column represents the number of chirps per 15 second (chirp frequency) and the second column represents the temperature Part 1 (5 points): Read the data from the file and store it in two arrays, one for the chirp frequency and another for the temperature. Use the method StdDraw.point(x, y) from the library StdDraw.java to draw a scatter plot of the data Before you plot the points you will need to set the size of the plot and the pen size. To set the size of the plot you need to call the methods StdDraw.setXscale(minX, maxX) and StdDraw.setYscale(minY, maxY) where minX, maxX, minY, and maxY are the minimum and maximum of the chirp frequency and the temperature respectively. To set the pen size use StdDraw.setPenRadius(0.01]) Part 2 (15 points): Now that you have a scatter plot of the data, we can use linear regression to fit a line in this dataset. A simple linear regression is a very useful technique for fitting a straight line A straight line can be defined by the formula: where a is the slope and b is the intercept with y- axis. For this assignment x is the chirp frequency and y is the temperature In order to fit a line on the given dataset, you need to find coefficients a and b. To accomplish this using simple linear regression, a can be calculated as: a -correlation(x, y) * sd (y)/sd(x) and coefficient b can be calculated using formula: b mean(y)- amean(x) The sample standard deviation of a variable x (sd(x)) can be calculated as (x - mean(x) Where N is the number of samples for the variable. The correlation between two variables x and y can be calculated as: V* mean(x) * mean correlation(x,y) - (N-1)*sd(x) * sd(y) The file crickets.txt (available on eCampus) contains data for 15 crickets (use a final variable!). The first column represents the number of chirps per 15 second (chirp frequency) and the second column represents the temperature Part 1 (5 points): Read the data from the file and store it in two arrays, one for the chirp frequency and another for the temperature. Use the method StdDraw.point(x, y) from the library StdDraw.java to draw a scatter plot of the data Before you plot the points you will need to set the size of the plot and the pen size. To set the size of the plot you need to call the methods StdDraw.setXscale(minX, maxX) and StdDraw.setYscale(minY, maxY) where minX, maxX, minY, and maxY are the minimum and maximum of the chirp frequency and the temperature respectively. To set the pen size use StdDraw.setPenRadius(0.01]) Part 2 (15 points): Now that you have a scatter plot of the data, we can use linear regression to fit a line in this dataset. A simple linear regression is a very useful technique for fitting a straight line A straight line can be defined by the formula: where a is the slope and b is the intercept with y- axis. For this assignment x is the chirp frequency and y is the temperature In order to fit a line on the given dataset, you need to find coefficients a and b. To accomplish this using simple linear regression, a can be calculated as: a -correlation(x, y) * sd (y)/sd(x) and coefficient b can be calculated using formula: b mean(y)- amean(x) The sample standard deviation of a variable x (sd(x)) can be calculated as (x - mean(x) Where N is the number of samples for the variable. The correlation between two variables x and y can be calculated as: V* mean(x) * mean correlation(x,y) - (N-1)*sd(x) * sd(y)











