The following facts pertain to a non-cancelable lease agreement between Faldo Leasing Company and Monty Company, a lessee.
| Commencement date | | January 1, | |
| Annual lease payment due at the beginning of each year, beginning with January 1, | | $110,269 | |
| Residual value of equipment at end of lease term, guaranteed by the lessee | | $46,000 | |
| Expected residual value of equipment at end of lease term | | $41,000 | |
| Lease term | | 6 | years |
| Economic life of leased equipment | | 6 | years |
| Fair value of asset at January 1, | | $622,000 | |
| Lessors implicit rate | | 5 | % |
| Lessees incremental borrowing rate | | 5 | % |
The asset will revert to the lessor at the end of the lease term. The lessee uses the straight-line amortization for all leased equipment.
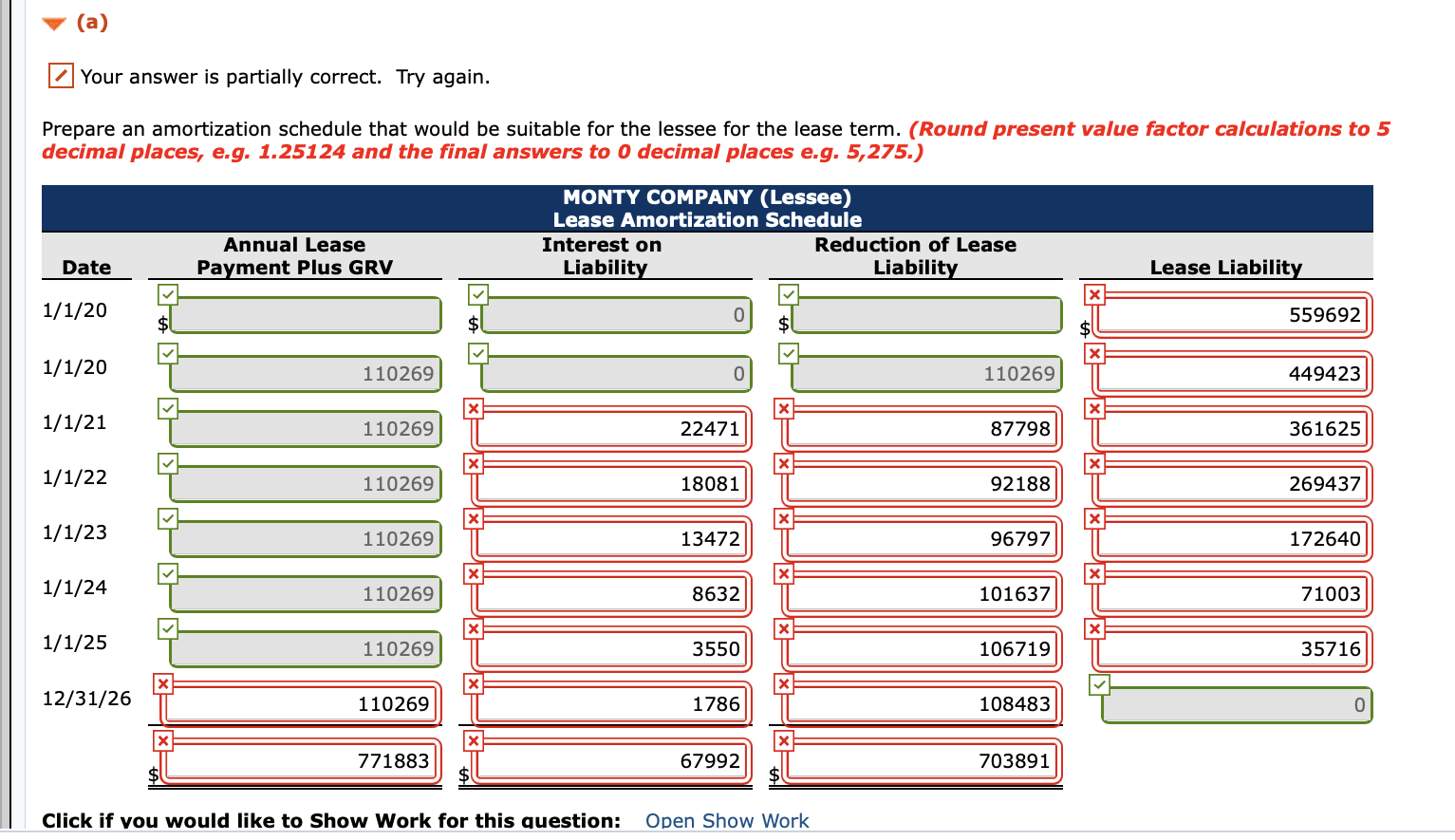
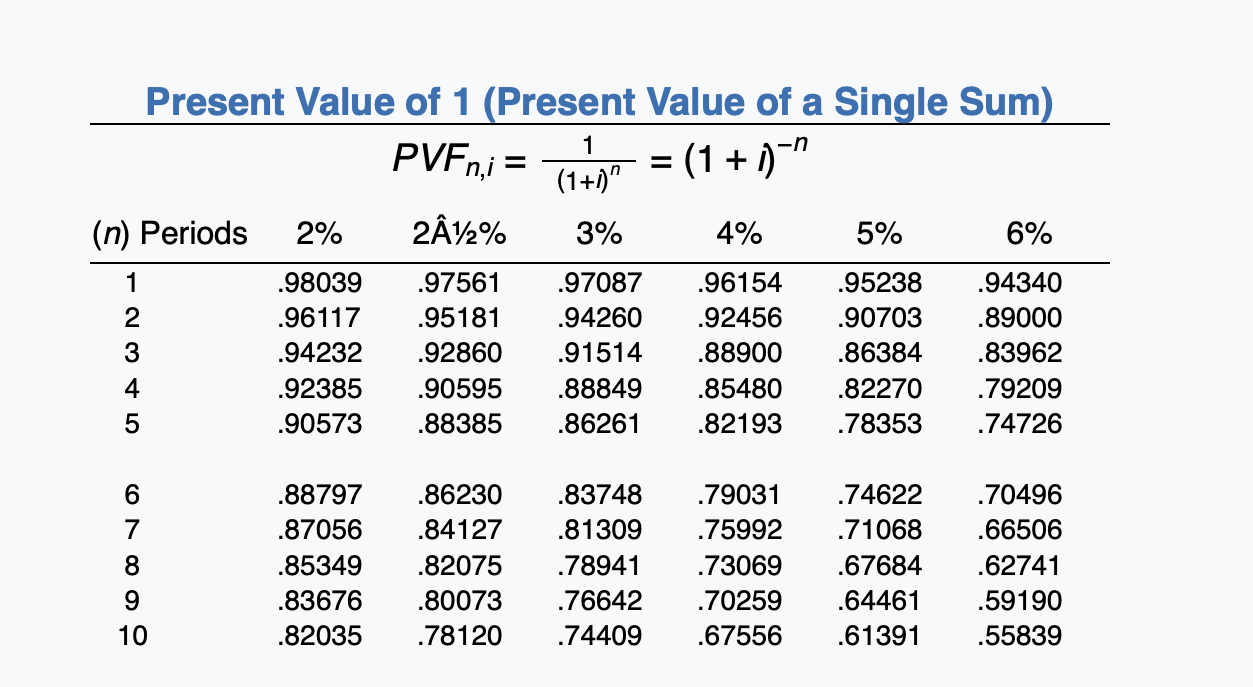

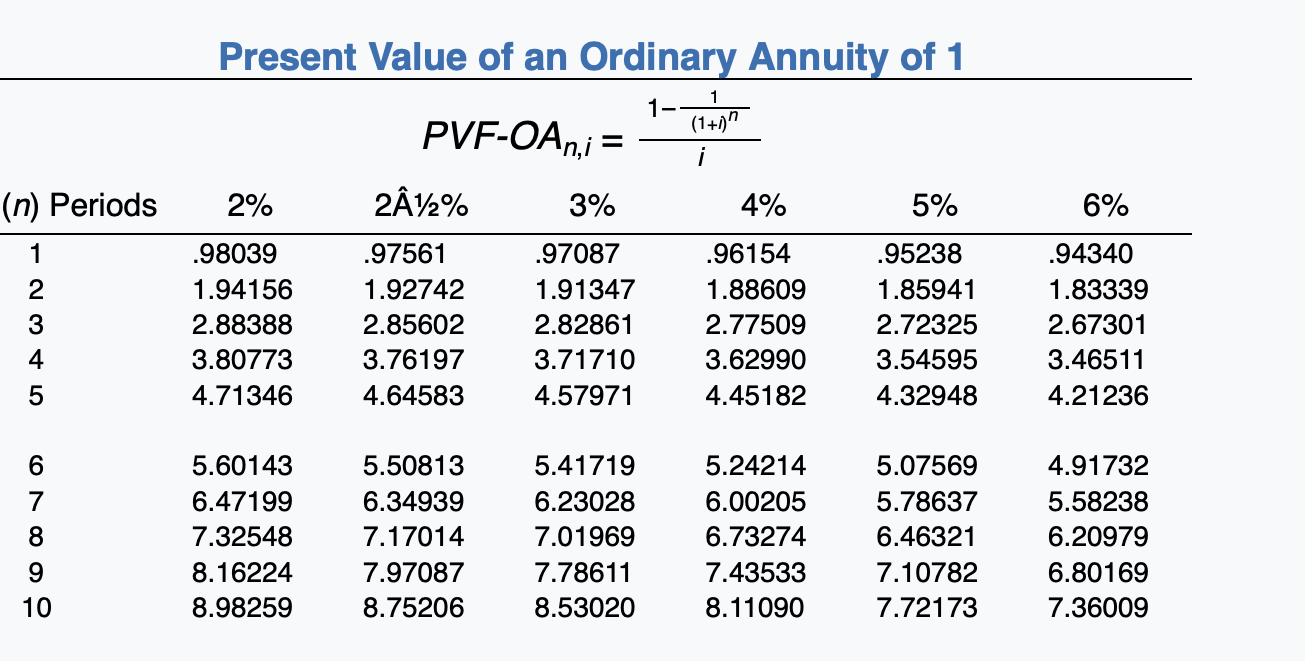
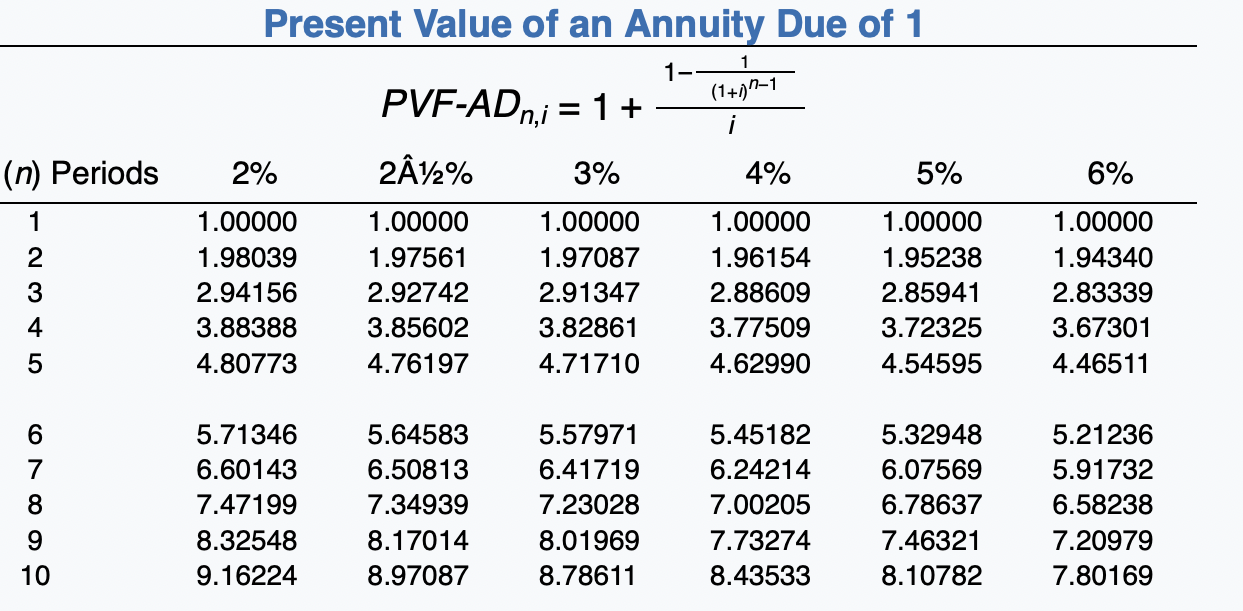
(a) Your answer is partially correct. Try again. Prepare an amortization schedule that would be suitable for the lessee for the lease term. (Round present value factor calculations to 5 decimal places, e.g. 1.25124 and the final answers to O decimal places e.g. 5,275.) MONTY COMPANY (Lessee) Lease Amortization Schedule Interest on Reduction of Lease Liability Liability Annual Lease Payment Plus GRV Date Lease Liability 1/1/20 0 559692 $1 $ 1/1/20 110269 110269 449423 x x x 1/1/21 110269 22471 87798 361625 X X x 1/1/22 110269 18081 92188 269437 x x 1/1/23 110269 13472 96797 172640 x 1/1/24 110269 8632 101637 71003 x x 1/1/25 110269 3550 106719 35716 X x 12/31/26 110269 1786 108483 0 x X x 771883 67992 703891 $ $ Click if you would like to Show Work for this question: Open Show Work PVF 1,1 = Present Value of 1 (Present Value of a Single Sum) 1 = (1 + 1)" (1+1)" (n) Periods 2% 212% 3% 4% 5% 6% 1 .98039 .97561 .97087 .96154 .95238 .94340 2 .96117 .95181 94260 .92456 .90703 .89000 3 .94232 .92860 .91514 .88900 .86384 .83962 4 .92385 .90595 .88849 .85480 .82270 .79209 5 .90573 .88385 .86261 .82193 .78353 .74726 6 7 8 9 10 .88797 .87056 .85349 .83676 .82035 .86230 .84127 .82075 .80073 78120 .83748 .81309 .78941 .76642 .74409 .79031 .75992 .73069 ..70259 .67556 .74622 .71068 .67684 .64461 .61391 .70496 .66506 .62741 .59190 .55839 Future Value of an Ordinary Annuity of 1 (1+1)"-1 FVF-OAni = (n) Periods 2% 2A%% 3% 4% 5% 6% 1 2 3 4 5 1.00000 2.02000 3.06040 4.12161 5.20404 1.00000 2.02500 3.07563 4.15252 5.25633 1.00000 2.03000 3.09090 4.18363 5.30914 1.00000 2.04000 3.12160 4.24646 5.41632 1.00000 2.05000 3.15250 4.31013 5.52563 1.00000 2.06000 3.18360 4.37462 5.63709 6 7 8 9 10 6.30812 7.43428 8.58297 9.75463 10.94972 6.38774 7.54743 8.73612 9.95452 11.20338 6.46841 7.66246 8.89234 10.15911 11.46338 6.63298 7.89829 9.21423 10.58280 12.00611 6.80191 8.14201 9.54911 11.02656 12.57789 6.97532 8.39384 9.89747 11.49132 13.18079 Present Value of an Ordinary Annuity of 1 1 1- PVF-OAni = (177)" i (n) Periods 2% 212% 3% 4% 5% 6% 1 2 3 4 .98039 1.94156 2.88388 3.80773 4.71346 .97561 1.92742 2.85602 3.76197 4.64583 .97087 1.91347 2.82861 3.71710 4.57971 .96154 1.88609 2.77509 3.62990 4.45182 .95238 1.85941 2.72325 3.54595 4.32948 .94340 1.83339 2.67301 3.46511 4.21236 5 6 7 8 5.60143 6.47199 7.32548 8.16224 8.98259 5.50813 6.34939 7.17014 7.97087 8.75206 5.41719 6.23028 7.01969 7.78611 8.53020 5.24214 6.00205 6.73274 7.43533 8.11090 5.07569 5.78637 6.46321 7.10782 7.72173 4.91732 5.58238 6.20979 6.80169 7.36009 9 10 Present Value of an Annuity Due of 1 1 1- (1+11-1 i PVF-ADni = 1 + 242% 3% (n) Periods 2% 4% 5% 6% 1 2 3 4 1.00000 1.98039 2.94156 3.88388 4.80773 1.00000 1.97561 2.92742 3.85602 4.76197 1.00000 1.97087 2.91347 3.82861 4.71710 1.00000 1.96154 2.88609 3.77509 4.62990 1.00000 1.95238 2.85941 3.72325 4.54595 1.00000 1.94340 2.83339 3.67301 4.46511 5 6 7 8 5.71346 6.60143 7.47199 8.32548 9.16224 5.64583 6.50813 7.34939 8.17014 8.97087 5.57971 6.41719 7.23028 8.01969 8.78611 5.45182 6.24214 7.00205 7.73274 8.43533 5.32948 6.07569 6.78637 7.46321 8.10782 5.21236 5.91732 6.58238 7.20979 7.80169 9 10 6% Future Value of 1 (Future Value of a Single Sum) FVFn,i = (1 + i)" (n) Periods 2% Z12% 3% 4% 5% 1 1.02000 1.02500 1.03000 1.04000 1.05000 2 1.04040 1.05063 1.06090 1.08160 1.10250 3 1.06121 1.07689 1.09273 1.12486 1.15763 4 1.08243 1.10381 1.12551 1.16986 1.21551 5 1.10408 1.13141 1.15927 1.21665 1.27628 1.06000 1.12360 1.19102 1.26248 1.33823 6 7 8 1.12616 1.14869 1.17166 1.19509 1.21899 1.15969 1.18869 1.21840 1.24886 1.28008 1.19405 1.22987 1.26677 1.30477 1.34392 1.26532 1.31593 1.36857 1.42331 1.48024 1.34010 1.40710 1.47746 1.55133 1.62889 1.41852 1.50363 1.59385 1.68948 1.79085 9 10












