The following formula predicts for linear probing the average number of probes needed for an unsuccessful search in a hash table with a load factor of ?:

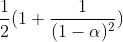
a) If the hash table is 80% full, what is the average number of probes needed to determine that a given key is not in the table?

b) Suppose that we are to store 10,000 keys in a hash table that has a capacity of 11,000. For this configuration, what is the average number of probes needed to determine that a given key is not in the table?

c) Are we better off storing the 10,000 keys in a balanced binary search tree (BST) instead of a hash table of size 11,000? Please justify your answer by considering the worst case complexity of searching a balanced BST.

(1 a)2 N