The following is the Equation 1.6 and Example 1.4 stated in the question to help solve the Problem 6.
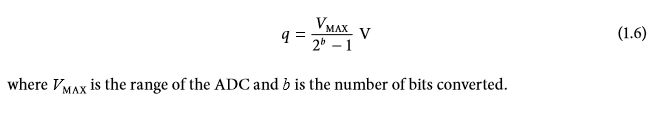
(1.6) where V Max is the range of the ADC and b is the number of bits converted, EXAMPLE 1.4 Write a MATLAB program to evaluate Equation 1.8 through simulation. Generate a 4-Hz sine wave in a 1000-point array (N=1000). Assume a sample interval of T, -0.002. Quantize this sine wave array into a 6-bit binary number using the routine quantization.m." The calling structure for this routine is signal_out=quantization (signal_in, bits) where signal_in is the original signal, bits is the number of bits for quantization (bits = 6 in this case), and signal_out is the quantized signal. Find the noise signal by subtracting the original signal from the quantized signal. Plot this signal and take the variance to quantify the noise. Then evaluate the theoretical noise using Equations 1.6 and 1.8 to find the theoretical variance and compare the two results. Solution Since the number of points desired is given, it is easier to generate a 1000-point time vector and then multiply it by T, that is, t = (0:999) *Ts. Then use that vector to generate the desired 4-Hz sine wave signal as in Example 1.2. (Note that almost any waveform and sample interval will work as long as it includes a fair number of points: the sine wave is just a handy waveform.) Quantize the signal into 6 bits using the routine quantization.m. Subtract the original sig. nal from the quantized signal and take the variance of the result as the simulated noise variance. Then evaluate Equation 1.6 with bits = 6 to find the quantization level, and use that value of q in conjunction with Equation 1.8 to find the theoretical value of noise variance. Compare the two results. Use a formatted output to ensure that the results are displayed in an adequate num- ber of decimal places. Example 1.4 Evaluate the quantization equation, Eq. 1.8 using simulated data. * Desired frequency N=1000; & Number of points Ts -0.002; Ts bits = 6; Quantization level t = (0:N-1) *Ts; # Vector used to generate 1-cycle sine wave signal in=sin(2*pi*f*t); Generate signal signal_out = quantization (signal_in, bits); Quantize signal noise_signal signal out - signal_in; Determine quantization error "The MATLAB routine quantization.m, like all auxiliary routines, can be found in this book's website. For clar ity, MATLAB variables, files, instructions, and routines are shown in courier typeface throughout the book. Biosignal and Medical Image Processing q noise = var (noise_signal); Variance of quantization noise q=1/(2abita - 1); Calculate quantization level (Eq. 1.6) theoretical = (-2)/12; Theoretical quantization error (Bq. 1.8) diap(' Quantization Noise) disp('Bits Emperical Theoretical') out = sprintf('82d 85e 85e', bits, q_noise, theoretical); Format output diap (out) 6. Semmlow Ch. 1 Problem #1.6. Change the quanitization.m function so that it also takes the analog voltage maximum and minimum as input arguments as well. Write a MATLAB problem to test Equation 1.6 through simulation. Generate a 5-Hz, 1200- point sine wave as in Example 1.4 assuming a sample interval of Ts= 0.002. Use quantization.m to digitize it using 4-, 8-, 12-, and 16-bit ADC. Then, as in Example 1.4, subtract the original signal from the quantized signal to find the error signal. The amplitude of the error signal should be equal to the quantization level, q in Equation 1.6. Use MATLAB's max and min functions to find this amplitude and compare it with the value predicted by Equation 1.6. Put this code in a for-loop and repeat the evaluations for the four different bit levels requested. Be sure to display the results to at least four decimal places to make an accurate comparison. (Hint: Most of the code needed for this problem will be similar to that in Example 1.4.] (1.6) where V Max is the range of the ADC and b is the number of bits converted, EXAMPLE 1.4 Write a MATLAB program to evaluate Equation 1.8 through simulation. Generate a 4-Hz sine wave in a 1000-point array (N=1000). Assume a sample interval of T, -0.002. Quantize this sine wave array into a 6-bit binary number using the routine quantization.m." The calling structure for this routine is signal_out=quantization (signal_in, bits) where signal_in is the original signal, bits is the number of bits for quantization (bits = 6 in this case), and signal_out is the quantized signal. Find the noise signal by subtracting the original signal from the quantized signal. Plot this signal and take the variance to quantify the noise. Then evaluate the theoretical noise using Equations 1.6 and 1.8 to find the theoretical variance and compare the two results. Solution Since the number of points desired is given, it is easier to generate a 1000-point time vector and then multiply it by T, that is, t = (0:999) *Ts. Then use that vector to generate the desired 4-Hz sine wave signal as in Example 1.2. (Note that almost any waveform and sample interval will work as long as it includes a fair number of points: the sine wave is just a handy waveform.) Quantize the signal into 6 bits using the routine quantization.m. Subtract the original sig. nal from the quantized signal and take the variance of the result as the simulated noise variance. Then evaluate Equation 1.6 with bits = 6 to find the quantization level, and use that value of q in conjunction with Equation 1.8 to find the theoretical value of noise variance. Compare the two results. Use a formatted output to ensure that the results are displayed in an adequate num- ber of decimal places. Example 1.4 Evaluate the quantization equation, Eq. 1.8 using simulated data. * Desired frequency N=1000; & Number of points Ts -0.002; Ts bits = 6; Quantization level t = (0:N-1) *Ts; # Vector used to generate 1-cycle sine wave signal in=sin(2*pi*f*t); Generate signal signal_out = quantization (signal_in, bits); Quantize signal noise_signal signal out - signal_in; Determine quantization error "The MATLAB routine quantization.m, like all auxiliary routines, can be found in this book's website. For clar ity, MATLAB variables, files, instructions, and routines are shown in courier typeface throughout the book. Biosignal and Medical Image Processing q noise = var (noise_signal); Variance of quantization noise q=1/(2abita - 1); Calculate quantization level (Eq. 1.6) theoretical = (-2)/12; Theoretical quantization error (Bq. 1.8) diap(' Quantization Noise) disp('Bits Emperical Theoretical') out = sprintf('82d 85e 85e', bits, q_noise, theoretical); Format output diap (out) 6. Semmlow Ch. 1 Problem #1.6. Change the quanitization.m function so that it also takes the analog voltage maximum and minimum as input arguments as well. Write a MATLAB problem to test Equation 1.6 through simulation. Generate a 5-Hz, 1200- point sine wave as in Example 1.4 assuming a sample interval of Ts= 0.002. Use quantization.m to digitize it using 4-, 8-, 12-, and 16-bit ADC. Then, as in Example 1.4, subtract the original signal from the quantized signal to find the error signal. The amplitude of the error signal should be equal to the quantization level, q in Equation 1.6. Use MATLAB's max and min functions to find this amplitude and compare it with the value predicted by Equation 1.6. Put this code in a for-loop and repeat the evaluations for the four different bit levels requested. Be sure to display the results to at least four decimal places to make an accurate comparison. (Hint: Most of the code needed for this problem will be similar to that in Example 1.4.]
