The following knapsack problem:

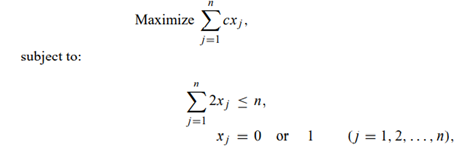
which has the same ‘‘contribution’’ for each item under consideration, has proved to be rather difficult to solve for most general-purpose integer-programming codes when n is an odd number.

a) What is the optimal solution when n is even? when n is odd?

 b) Comment specifically on why this problem might be difficult to solve on general integer-programming codes when n is odd.

subject to: Maximize Scxj, j=1 2x, n, j=1 x, = 0 or 1 (j = 1, 2,..., n),