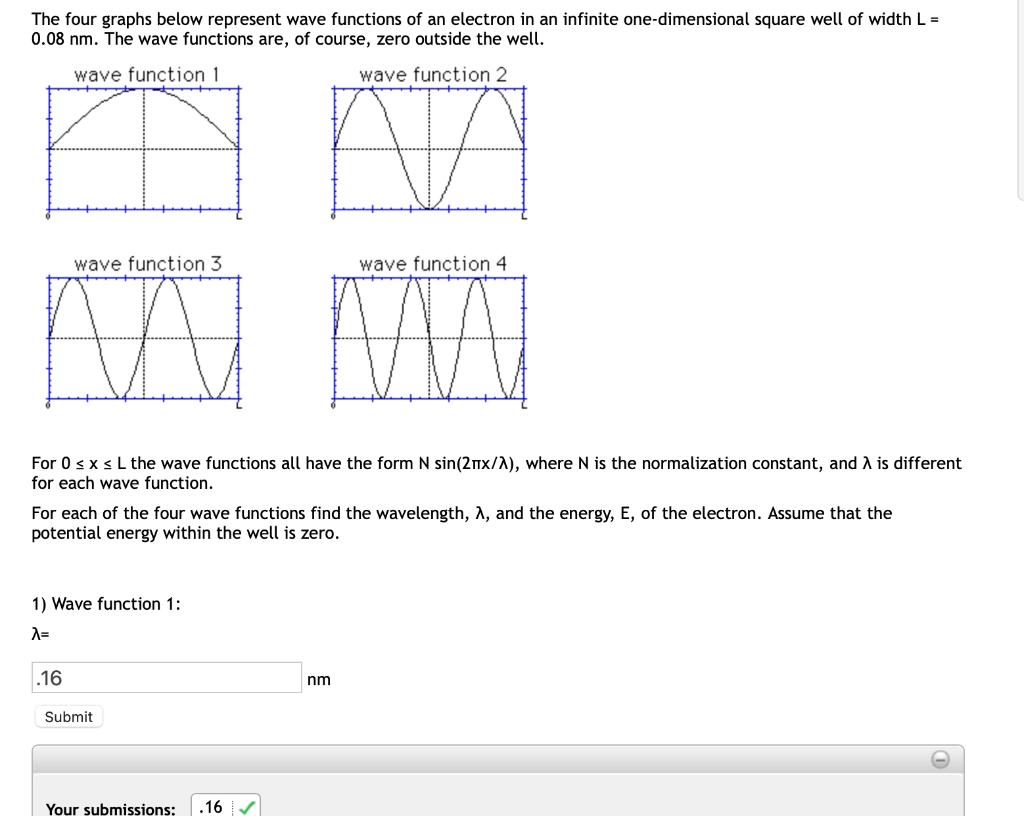
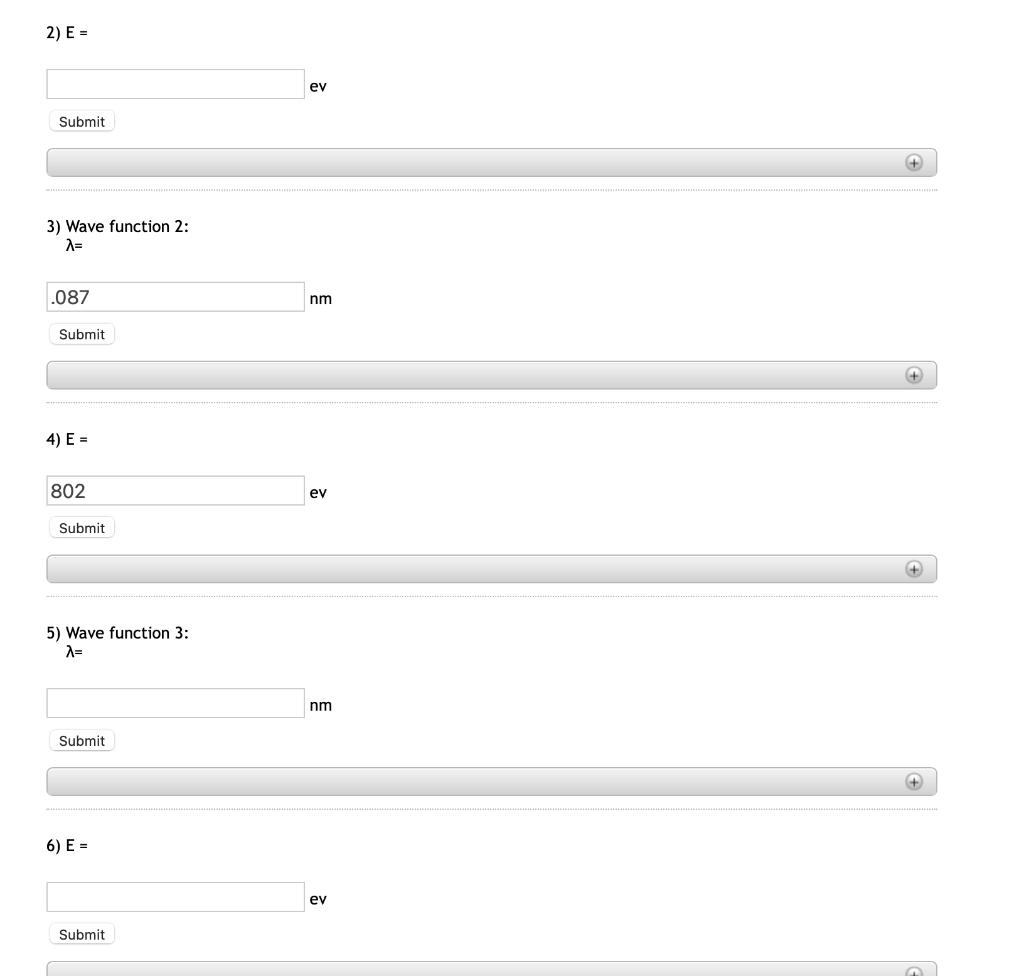
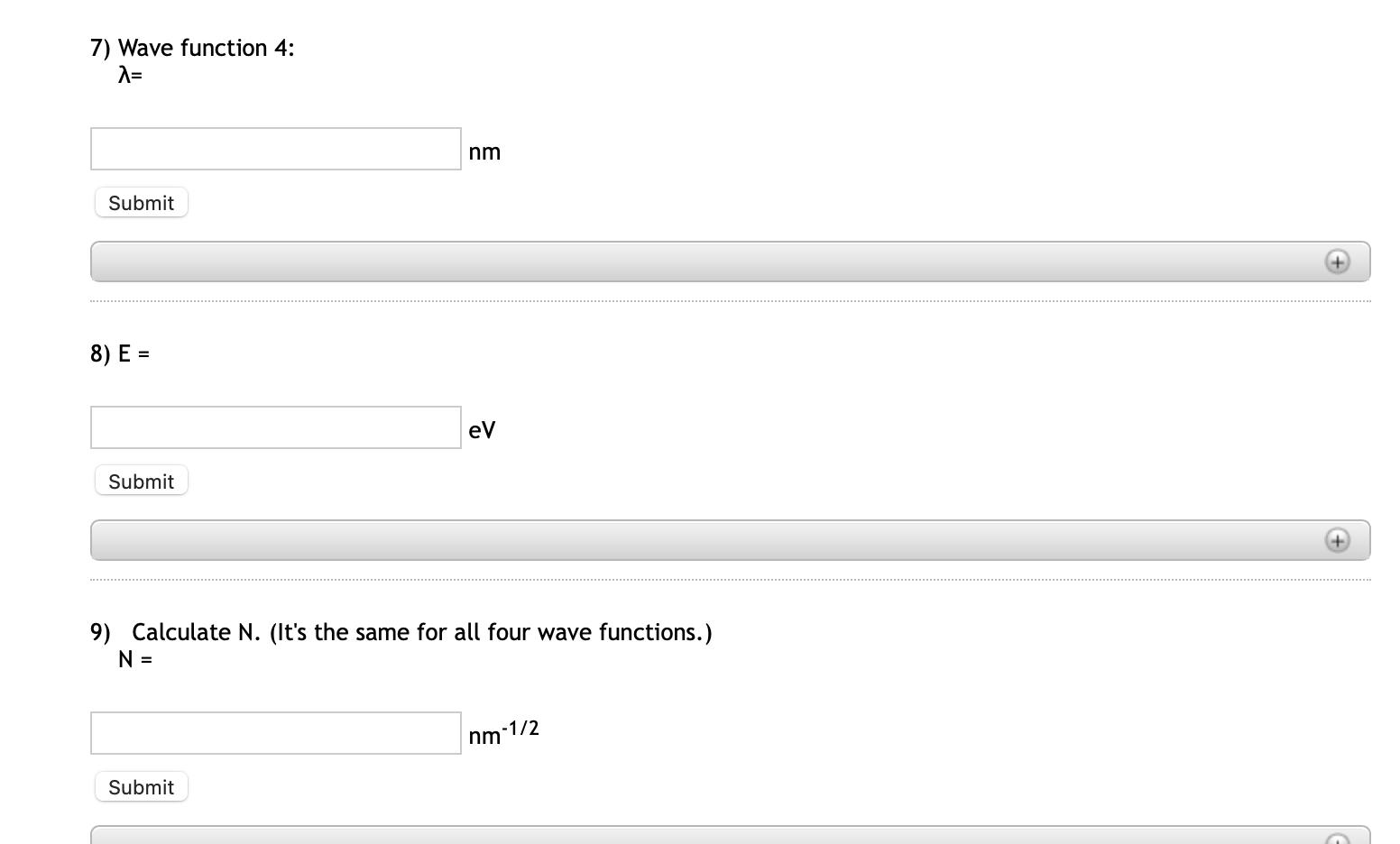
The four graphs below represent wave functions of an electron in an infinite one-dimensional square well of width L = 0.08 nm. The wave functions are, of course, zero outside the well. wave function 1 wave function 2 wave function 3 wave function 4 For 0 sx s L the wave funct for each wave function. sin(2nx/A), mormalization constant, and A is diffe For each of the four wave functions find the wavelength, A, and the energy, E, of the electron. Assume that the potential energy within the well is zero. 1) Wave function 1: A= .16 nm Submit Your submissions: .16 2) E = ev Submit + 3) Wave function 2: A= .087 nm Submit 4) E = 802 ev Submit 5) Wave function 3: A= nm Submit + 6) E = ev Submit 7) Wave function 4: A= nm Submit 8) E = eV Submit 9) Calculate N. (It's the same for all four wave functions.) N = nm -1/2 Submit