Question
The Game of Life is a well- known mathematical game that gives rise to amazingly complex behavior, although it can be specif ied by a
The Game of Life is a well-
known mathematical game that gives rise to amazingly complex
behavior, although it can be specif
ied by a few simple rules. (It is not actually a game in the
traditional sense, with players competing for a win.) Here are the rules. The game is played on a
rectangular board. Each square can be either empty or occupied. At the beginning, you can
specify
empty and occupied cells in some way; then the game runs automatically. In each
generation, the next generation is computed. A new cell is born on an
empty square if it is surrounded by exactly three occupied neighbor
cells. A cell dies of overcrowding if
it is surrounded by four or more
neighbors, and it dies of loneliness if it is surrounded by zero or one
neighbor. A neighbor is an occupant of an adjacent square to the left,
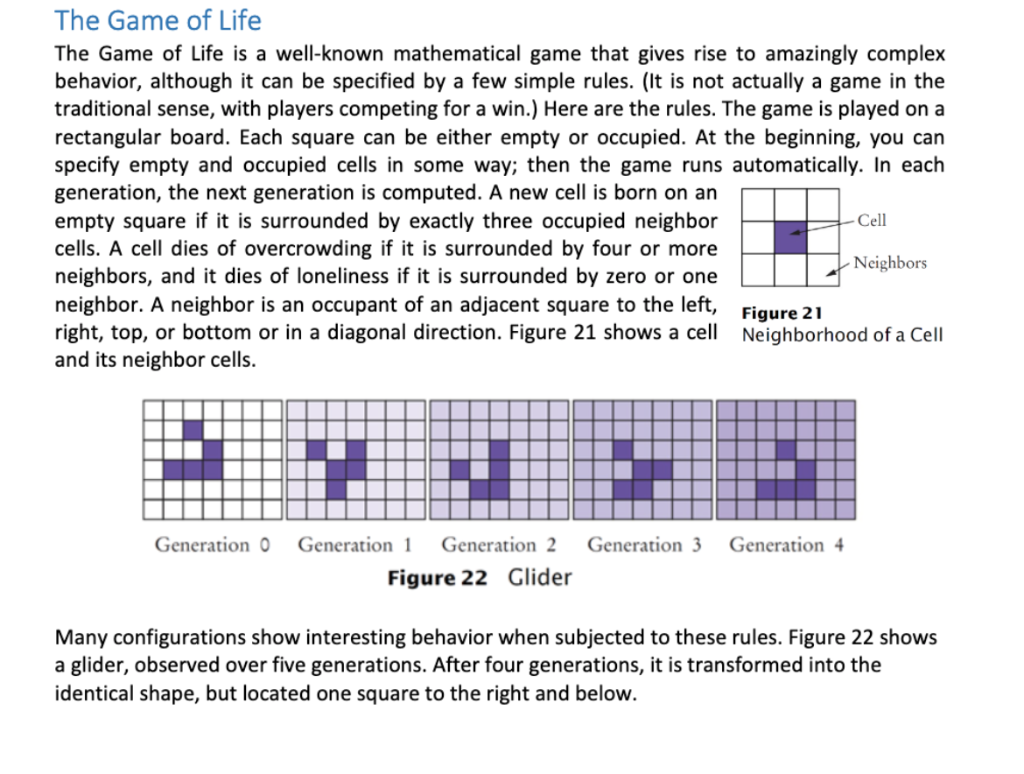
right, top, or bottom or in a diagonal direction. Figure 21 shows a cell
and its neighbor cells.

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


