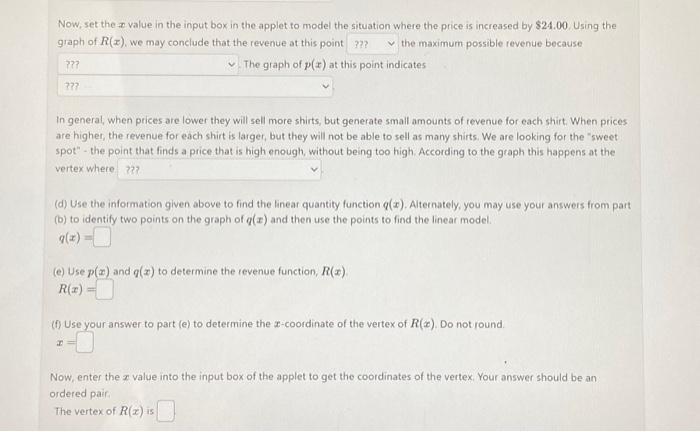
The IUP Future Entrepreneurs Club (FEC) is selling t-shirts to raise money to fund Club activities. They find that if they set their selling orice at $10.72 then they will sell 37 t-shirts. They also find that for each $1.00 increade in the selling price, the Club will sell one fewer shirt.
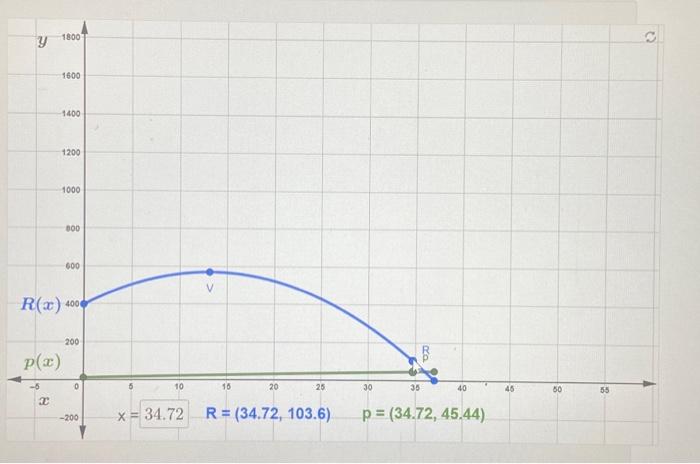
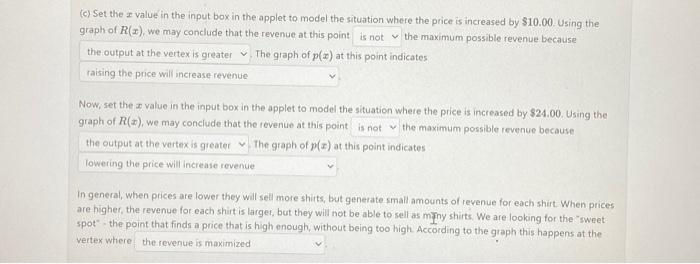
The IUP. Future Entrepreneurs Club (FEC) is selling t shirts to raise money to fund Club activities. They find that if they set theit selling price at $10.72 then they will sell 37 t-shirts. They also find that for each $1.00 increase in the selling price, the Club will sell one fewer shirt. In the applet above, x represents the number of $1.00 increases in the selling price of each t-shirt, p(x) (in green) represents the selling price of the t-shirts in dollars, and R(x) (in blue) is the total revenue generated from shirt sales, in dollars. The function q(x) gives the number (quantity) of tshirts that FEC sells q(x) is not provided in the applet, as you will find it in one of the parts below. (a) Use the information given above to find the linear price function p(x). Alternately, you may use the applet to identify two points on the graph of p(x) and then use the points to find the linear model. p(x)= (b) Suppose that the FEC decides to increase the price of each t-shirt by $10.00. Then, the new selling price will bes and the t-shirt sales will generate a revenue of: This means they will sell t-shirts at the new price. Now, suppose instead that the FEC decides to increase the price of each t-shirt by $24.00. Then, the new selling price will be and the t-shirt sales will generate a revenue of $ This means they will sell t-shirts at the new price. (c) Set the x value in the input box in the applet to model the situation where the price is increased by $10.00. Using the graph of R(x), we may conclude that the revenue at this point the maximum possible revenue because The graph of p(x) at this point indicates Now, set the x value in the input box in the applet to model the situation where the price is increased by $24.00. Using the graph of R(x). we may conclude that the revenue at this point the maximum possible revenue because The graph of p(x) at this point indicates In general, when prices are lower they will sell more shirts, but generate small amounts of revenue for each shirt. When prices are higher, the revenue for each shirt is larger, but they will not be able to sell as many shirts. We are looking for the "sweet spot" - the point that finds a price that is high enough, without being too high. According to the graph this happens at the vertex where (d) Use the information given above to find the linear quantity function q(x). Alternately, you may use your answers from part (b) to identify two points on the graph of q(x) and then use the points to find the linear model. g(x)= (e) Use p(x) and q(x) to determine the revenue function, R(x) R(x)= (f) Use your answer to part (e) to determine the x-coordinate of the vertex of R(x). Do not round. x= Now, enter the x value into the input box of the applet to get the coordinates of the vertex. Your answer should be an ordered pair. The vertex of R(x) is (g) The FEC concludes that in order to maximize revenue, the selling price for the t-shirts should be ? At this price, they can expect to earn a maximum possible revenue of s The IUP Future Entrepreneurs Club (FEC) is selling t-shirts to raise money to fund Club activities. They find that if they set their selling price at $10.72 then they will sell 37t-shirts. They also find that for each $1.00 increase in the selling price, the Club will sell one fewer shirt In the applet above, x represents the number of $1.00 increases in the selling price of each t shirt, p(x) (in green) represents the selling price of the t-shirts in dollars, and R(x) (in blue) is the total revenue generated from shirt sales, in dollars. The function q(x) gives the number (quantity) of t-shirts that FEC sells. q(x) is not provided in the applet, as you will find it in one of the parts below. (a) Use the information given above to find the linear price function p(x). Alternately, you may use the applet to identify two points on the graph of p(x) and then use the points to find the linear model. p(x)==10.72+x (b) Suppose that the FEC decides to increase the price of each t-shirt by $10.00. Then, the new selling price will be $ and the t-shirt sales will generate a revenue of $ This means they will sell t-shirts at the new price. Now, suppose instead that the FEC decides to increase the price of each t-shirt by $24.00. Then, the new selling price will be and the t-shirt sales will generate a revenue of $ This means they will sell t-shirts at the new price. (c) Set the x value in the input box in the applet to model the situation where the price is increased by $10.00. Using the graph of R(x), we may conclude that the revenue at this point the maximum possible revenue because The graph of p(x) at this point indicates Now, set the x value in the input box in the applet to model the situation where the price is increased by $24.00, Using the graph of R(x), we may conclude that the revenue at this point the maximum possible revenue because The graph of p(x) at this point indicates In general, when prices are lower they will sell more shits, but generate small amounts of revenue for each shirt When prices are higher, the revenue for each shirt is larger, but they will not be able to sell as myny shirts. We are looking for the "sweetspot" - the point that finds a price that is high enouah. without being too high According to the graph this happens at the vertex where (d) Use the information given above to find the linear quantity function q(x). Alternately, you may use your answers from part (b) to identify two points on the graph of q(x) and then use the points to find the linear model. q(x)= (e) Use p(x) and q(x) to determine the revenue function, R(x). R(x)= (f) Use your answer to part (e) to determine the x coordinate of the vertex of R(x). Do not round x=37 Now, enter the x value into the input box of the applet to get the coordinates of the vertex. Your answer should be an ordered pair. The vertex of R(x) is (g) The FEC concludes that in order to maximize revenuc, the selling price for the t-shirts should be s they can expect to earn a maximum possible revenue of $ At this price