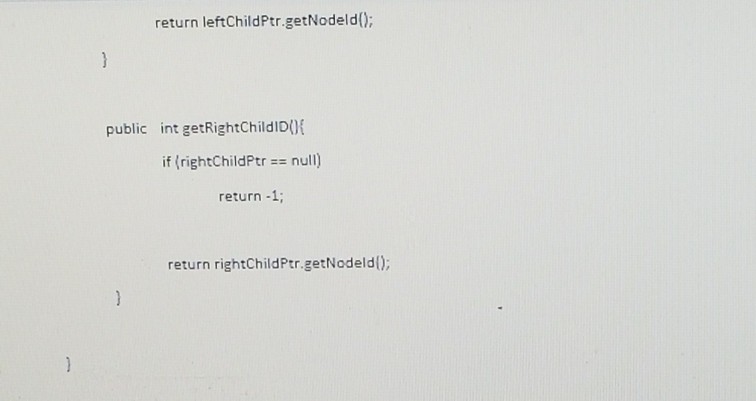
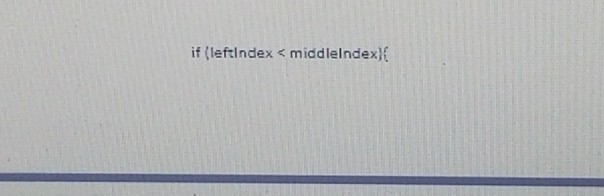
The lowest common ancestor (LCA) for two nodes A and B in a binary search tree (BST) is the node that is the common ancestor for both A and B, and is the farthest away from the root node of the BST. Note that depending on the BST, one of the two nodes A and B could themselves be the LCA of the other node or a third node (that is different from nodes A and B) could be the LCA. The three cases are illustrated in the following figure: 21 21 21 18 78 18 78 18 78 25 81 25 (81 25 81 12 24 (34 12 24) (34 12 (24 34 23 23 23 Node '6' with data 25 is the LCA for nodes 4' and '7' with data 23 and 34 respectively Node '6' with data 25 is the LCA for nodes 4' and '6' with data 23 and 25 respectively Node '3' with data 21 is the LCA for nodes 3' and '9' with data 21 and 81 respectively In this project. you will construct a BST based on a randomly generated and sorted array of integers input the values (i.e.. data) for two nodes A and B (that are part of the BST) and find the data corresponding to their LCA. Follow the steps below (1) You will first construct a BST using a randomly generated and sorted array (sorted using Selection sort). The code to construct such a BST is given to you (2) You will then input the data/values for the two search nodes A and B. Between the two node determine the node whose data is relatively lower and call such a node as the leftSearchNode; the other node will be then called the rightSearchNode. (3) The third and the major step is to initiate a search process starting from the root node (call prospectiveAncestorNode) ed say, the If the data for the leftSearchNode and rightSearchNode are both lower than that of the prospectiveAncestorNode, then the two nodes should be located in the left sub tree of the prospectiveAncestorNode. Hence, we set the id of the prospective ancestor node to correspond to the id of its left child and continue the seareh process in its left sub tree If the data for the leftSearchNode and rightSearchNode are both greater than that of the prospectiveAncestorNode, then the two nodes should be in the right sub tree of the prospectiveAncestor Node. Hence, we set the id of the prospective ancestor node to correspond to the id of its right child and continue the search process in its right sub tree