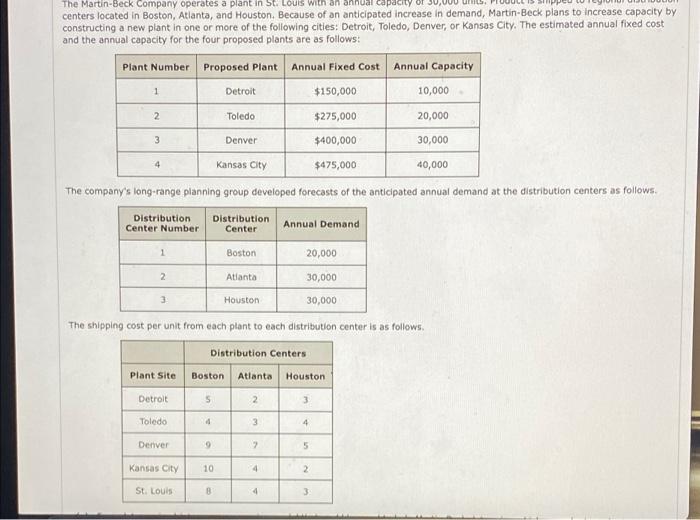
The Martin-Beck Company operates a plant in St. Louis with an annual capacity of su centers located in Boston, Atlanta, and Houston. Because of an anticipated increase in demand, Martin-Beck plans to increase capacity by constructing a new plant in one or more of the following cities: Detroit, Toledo, Denver, or Kansas City. The estimated annual fixed cost and the annual capacity for the four proposed plants are as follows: Plant Number Proposed Plant Annual Fixed Cost Annual Capacity 1 Detroit $150,000 10,000 2 Toledo $275,000 20,000 3 Denver $400,000 30,000 4 Kansas City $475,000 40,000 The company's long-range planning group developed forecasts of the anticipated annual demand at the distribution centers as follows. Distribution Center Number Distribution Center Annual Demand 1 Boston 20,000 2 Atlanta 30,000 3 Houston 30,000 The shipping cost per unit from each plant to each distribution center is as follows Distribution Centers Plant Site Boston Atlanta Houston Detroit 5 2 3 Toledo 4 4 Denver 9 2 5 Kansas City 10 2 St. Louis B 4 3 distribution center with the existing plant in St. Louis being plant number 5. Let y, - 1 if a plant is constructed in Detroit and o if not Y2 = 1 if a plant is constructed in Toledo and if not, y3 - 1 if a plant is constructed in Denver and o if not, and Y - 1 if a plant is constructed in Kansas City and O if not.) 23 + 5*33 + 10x1 +4x52 + 3x +150), +275y2 + 40093 +4 + + 9x31+ 7x32 + AXA2 +2x43 + 8451 Min st. Detroit Capacity *11+x12 + x13 - 10y, so Toledo Capacity *21 + x22 + x23 + 20y, so Denver Capacity *31 + x32 + x33 30y3 50 > *41+x12 + x43 407, 30 Kansas City Capacity |x31+x52 St. Louis Capacity 53 5 30 Boston Demand *11 + x2 + x31+ *41+x51 20 Atlanta Demand *12+ *22*32 + x^2 + x2 = 30 Houston *13+x23+ *33 +*23 +*53 + = 30 Demand O for all and and Yi Ya binary (b) Solve the model you formulated in part (a). What is the optimal cost (In $)? What is the optimal set of plants to open? (Select all that apply.) Detroit Toledo Denver Kansas City (c) Using equation (13.1), (Sum of variables in the set o) - sum of variables in the set z) = (number of variables in the set o) - 1 where is the set of binary variables in our original optimal solution set to one and Z is the set of those set to zero, find a second- best solution. What is the increase in cost (in $) versus the best solution from part (b)? $ 25000 X