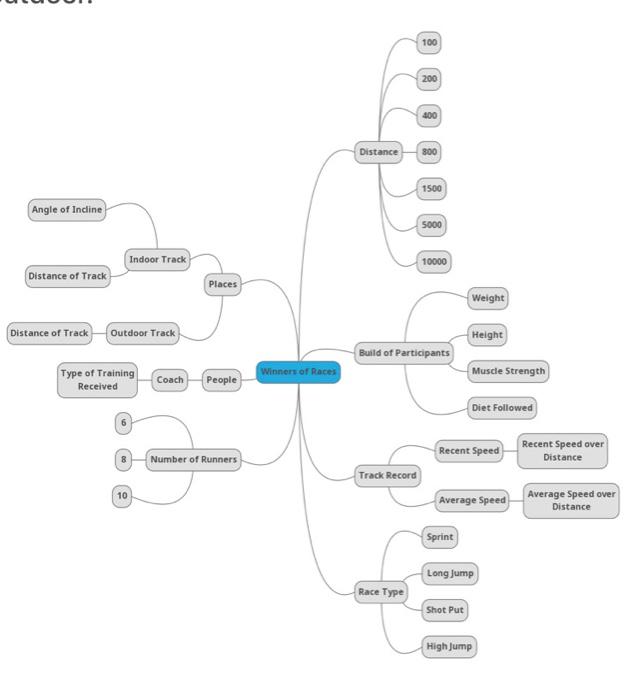
the mind map that been created is
5. a) Referring to the mind map you created for Question 2 write down a feature vector of THREE properties that represent a runner's data for predicting his or her chances in a given race. For EACH property, specify the "perfect" value that maximises the chances of a runner winning the race and the limiting values that represent the least chance of winning. Explain what each property is represent- ing and why you have chosen the particular perfect and limiting values. Note that this is similar to the GRIST and house DSSs studied in this module, which defined "perfect" values of each feature, such as the number of rooms re- quired in a house. These DSSs also specified the limiting values that determine how the fuzzy set membership grade (MG) is calculated for values deviating from the perfect one: that is partial matches with the perfect value. For exam- ple, (100) 17 1) (10 0.2) would represent a perfect value of 7 (MG of 1). an upper value of 10 with MG of 0.2 and a lower value of 0 with OMG. (10 marks) b) Explain how you could use fuzzy-set methods to determine the membership of a particular runner (e.g. Farah) in the perfect-runner (winner) class, as specified by the properties and values you gave in Part a Your answer should explain how each individual property's membership grade is calculated and how the overall runner's membership grade is generated from the individual ones using fuzzy set operators such as intersection or union or whatever you think works best. (10 marks) c) Write the Lisp code for a function called rate-runner that implements the methods described in Part 6 The function would take your list for a perfect runner and the property-value pairs list for a particular runner such as Farah and return the runner's chance of winning, which is the membership grade in the perfect-runner's class. You can assume that a function called get-mg exists already that takes a prop erty of your runner, the matching property in the perfect winner list and returns the property's membership grade in the perfect winner class as follows: > (get-mg property perfect-property) 0.4 (10 marks) 100 200 400 Distance 800 1500 Angle of Incline 5000 Indoor Track 10000 Distance of Track Places Weight Distance of Track Outdoor Track Height Build of Participants Type of Training Received Muscle Strength Winners of Races Coach People Diet Followed Recent Speed Recent Speed over Distance 8 Number of Runners Track Record 10 Average Speed Average Speed over Distance Sprint Long Jump Race Type Shot Put High Jump 5. a) Referring to the mind map you created for Question 2 write down a feature vector of THREE properties that represent a runner's data for predicting his or her chances in a given race. For EACH property, specify the "perfect" value that maximises the chances of a runner winning the race and the limiting values that represent the least chance of winning. Explain what each property is represent- ing and why you have chosen the particular perfect and limiting values. Note that this is similar to the GRIST and house DSSs studied in this module, which defined "perfect" values of each feature, such as the number of rooms re- quired in a house. These DSSs also specified the limiting values that determine how the fuzzy set membership grade (MG) is calculated for values deviating from the perfect one: that is partial matches with the perfect value. For exam- ple, (100) 17 1) (10 0.2) would represent a perfect value of 7 (MG of 1). an upper value of 10 with MG of 0.2 and a lower value of 0 with OMG. (10 marks) b) Explain how you could use fuzzy-set methods to determine the membership of a particular runner (e.g. Farah) in the perfect-runner (winner) class, as specified by the properties and values you gave in Part a Your answer should explain how each individual property's membership grade is calculated and how the overall runner's membership grade is generated from the individual ones using fuzzy set operators such as intersection or union or whatever you think works best. (10 marks) c) Write the Lisp code for a function called rate-runner that implements the methods described in Part 6 The function would take your list for a perfect runner and the property-value pairs list for a particular runner such as Farah and return the runner's chance of winning, which is the membership grade in the perfect-runner's class. You can assume that a function called get-mg exists already that takes a prop erty of your runner, the matching property in the perfect winner list and returns the property's membership grade in the perfect winner class as follows: > (get-mg property perfect-property) 0.4 (10 marks) 100 200 400 Distance 800 1500 Angle of Incline 5000 Indoor Track 10000 Distance of Track Places Weight Distance of Track Outdoor Track Height Build of Participants Type of Training Received Muscle Strength Winners of Races Coach People Diet Followed Recent Speed Recent Speed over Distance 8 Number of Runners Track Record 10 Average Speed Average Speed over Distance Sprint Long Jump Race Type Shot Put High Jump