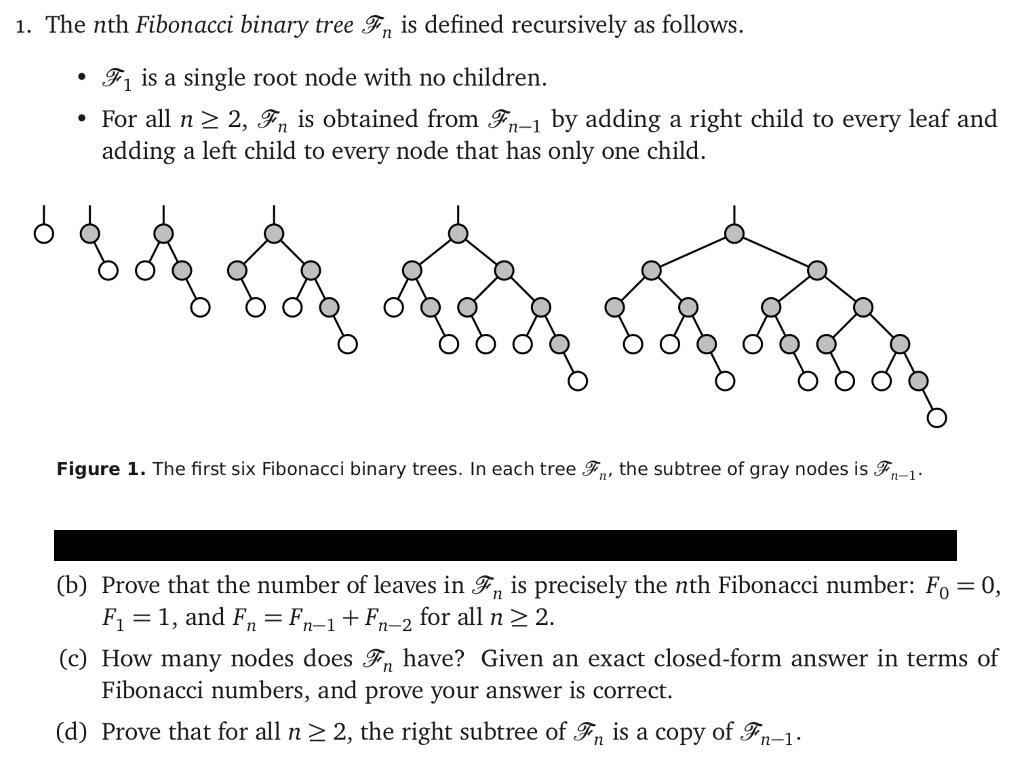
1. The nth Fibonacci binary tree F is defined recursively as follows. F is a single root node with no children. For all n 2, Fn is obtained from F-1 by adding a right child to every leaf and adding a left child to every node that has only one child. Figure 1. The first six Fibonacci binary trees. In each tree F, the subtree of gray nodes is F-1. (b) Prove that the number of leaves in F is precisely the nth Fibonacci number: Fo = 0, F = 1, and Fn = Fn-1 + Fn-2 for all n 2. (c) How many nodes does F have? Given an exact closed-form answer in terms of Fibonacci numbers, and prove your answer is correct. (d) Prove that for all n 2, the right subtree of Fn is a copy of Fn-1.