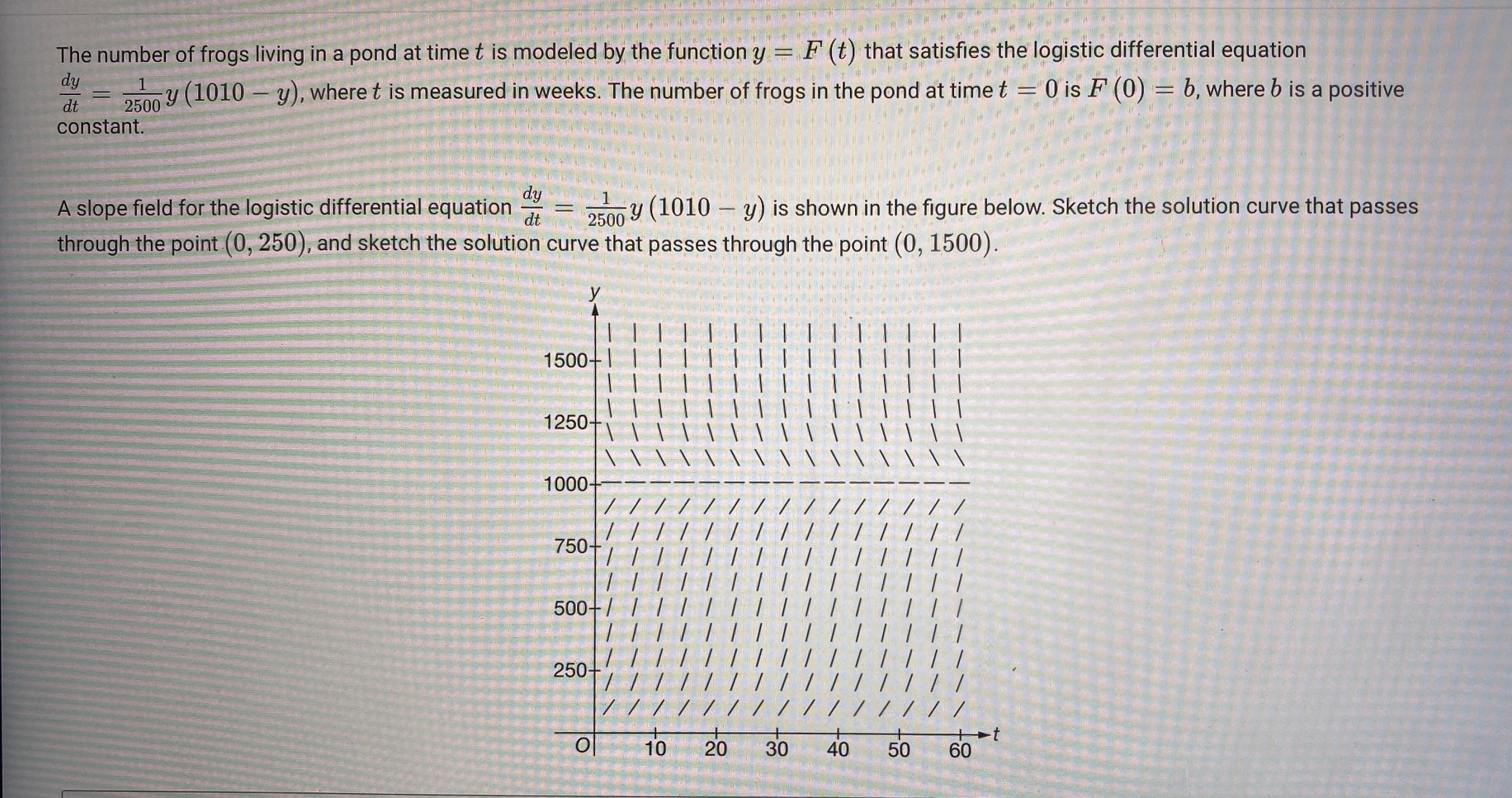
The number of frogs living in a pond at time t is modeled by the function y = F(t) that satisfies the logistic differential equation dy dt constant. 2500 y (1010 - y), where t is measured in weeks. The number of frogs in the pond at time t = 0 is F (0) = b, where b is a positive A slope field for the logistic differential equation dt 2500 y (1010y) is shown in the figure below. Sketch the solution curve that passes through the point (0, 250), and sketch the solution curve that passes through the point (0, 1500). 1500- 1250- 1000- 750- 500- 250- +20 10 20 30 t 30 40 50 60 (i) If b=250, what is the largest rate of increase in the number of frogs in the pond? Explain your reasoning, and indicate units of measure. (ii) If b = 750, what is the largest rate of increase in the number of frogs in the pond? Explain your reasoning, and indicate units of measure. B I U X2 X2 CN= 0/10000 Word Limit Let b=100. Use Euler's method, starting at t = weeks. Show the work that leads to your answer. O with two steps of equal size, to approximate F (4), the number of frogs in the pond at time t = BIU X2 X2 G C 0/10000 Word Limit Determine whether the approximation found in part (c) is an underestimate or an overestimate for the number of frogs in the pond at time t = 4 weeks, when b = 100. Explain your reasoning. B I 2 >