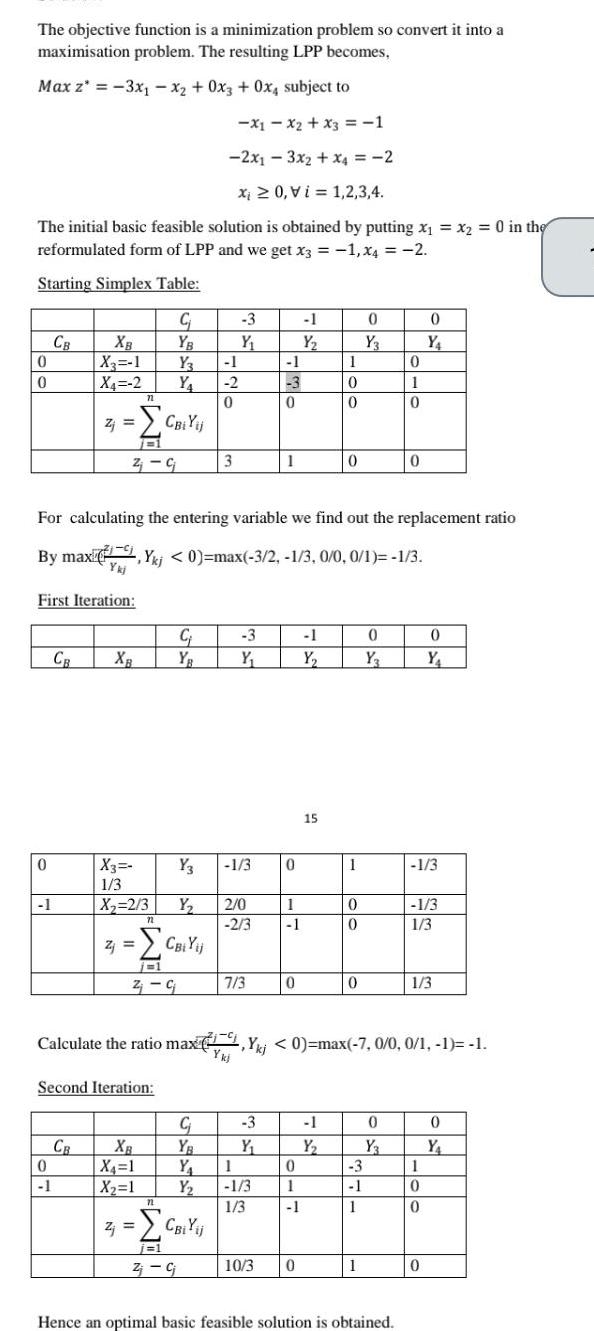
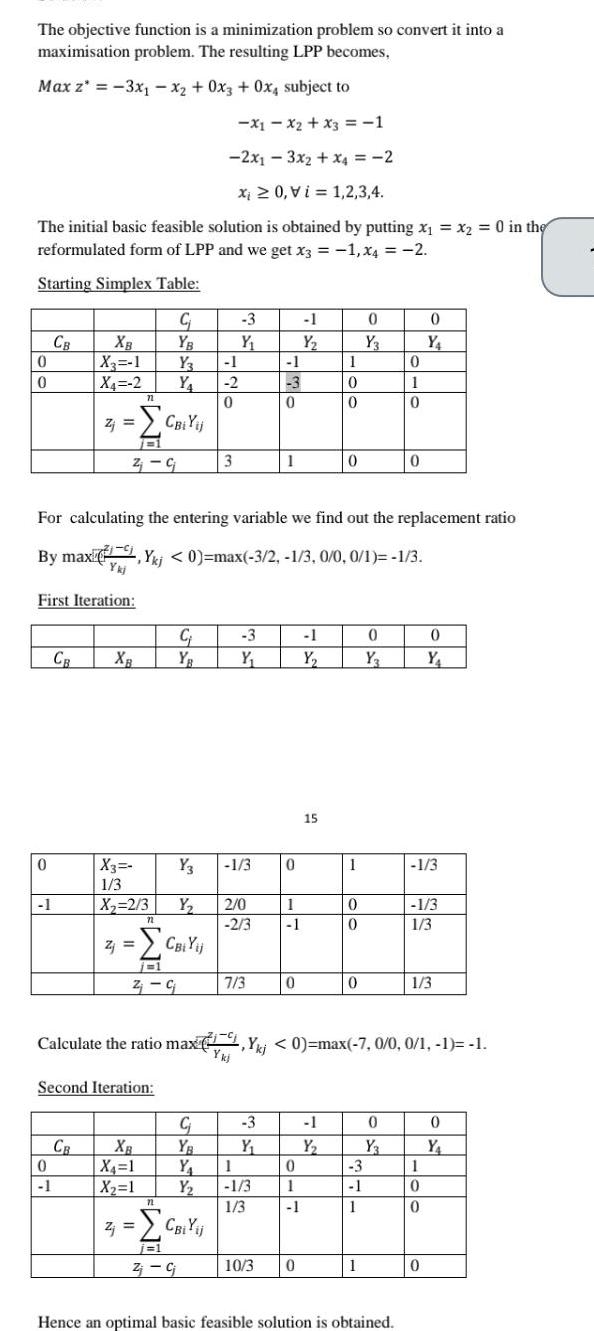
The objective function is a minimization problem so convert it into a maximisation problem The resulting LPP becomes Max z 3x x2 0x3 0x4 subject to X1X2 x3 1 2x13x2 x4 2 Xi 0 Vi 1 2 3 4 The initial basic feasible solution is obtained by putting x x2 0 in the reformulated form of LPP and we get x3 1 x4 2 Starting Simplex Table 0 0 0 CB 1 XB X 1 X4 2 First Iteration CB 0 1 Zj Z CB 71 n 7731 Z C XB X3 1 3 X 2 3 Second Iteration C YB Y Y Y3 Y Z CBi Yij j 1 2 G 72 XB X 1 X 1 CBi Yij For calculating the entering variable we find out the replacement ratio By max kj 0 max 3 2 1 3 0 0 0 1 1 3 72 C 1 2 0 3 3 Y Z CBiYij j 1 Z cj 3 Y 1 3 2 0 2 3 7 3 C YB Y 1 Y 1 3 1 3 3 Y 1 3 0 1 10 3 0 1 1 0 1 Y 0 1 1 0 1 Y 15 1 0 0 0 1 Y 1 7 9 Calculate the ratio max kj 0 max 7 0 0 0 1 1 1 Ykj 0 0 0 0 Y3 3 1 1 1 0 Y 0 1 0 0 Y3 0 Hence an optimal basic feasible solution is obtained 0 Y 1 3 0 Y 1 3 1 3 1 3 1 0 0 0 0 Y