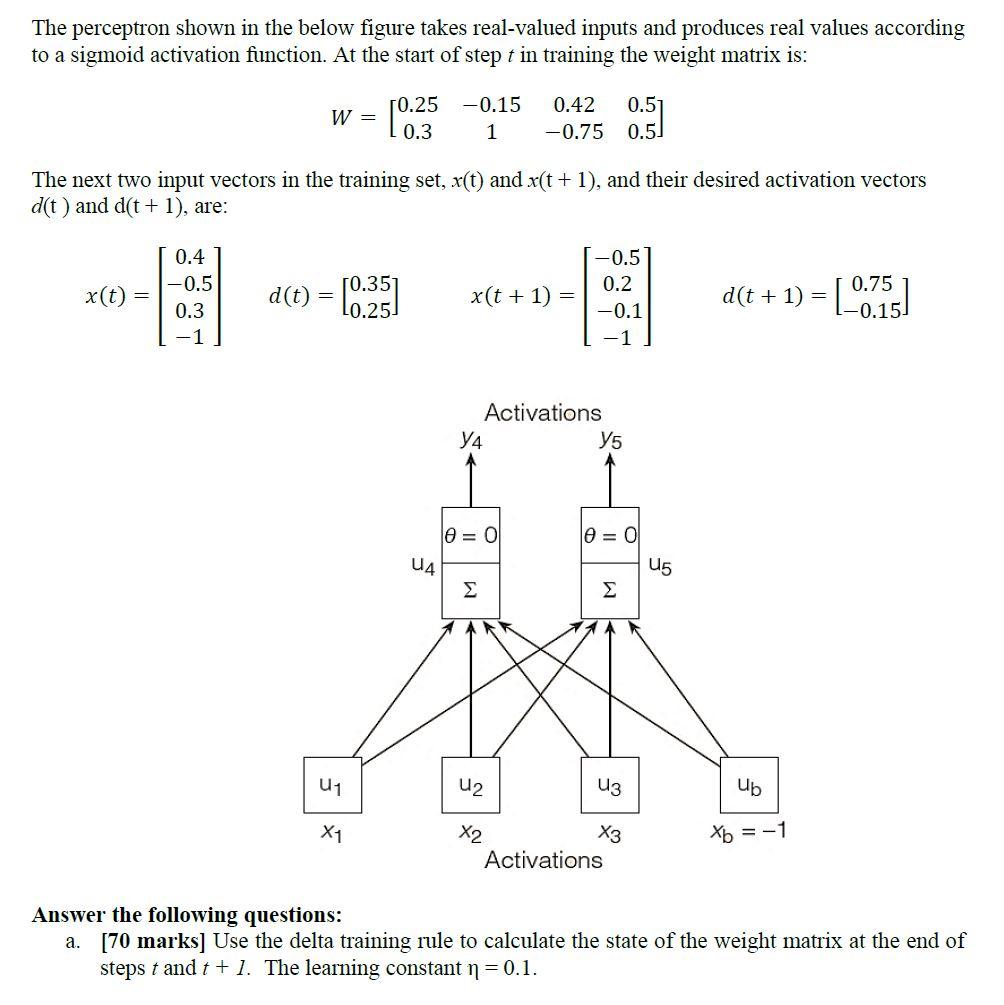
The perceptron shown in the below figure takes real-valued inputs and produces real values according to a sigmoid activation function. At the start of step t in training the weight matrix is: W= 0.5 T0.25 0.3 [0.25 -0.15 1 0.42 -0.75 0.5) The next two input vectors in the training set, x(t) and x(t + 1), and their desired activation vectors d(t) and d(t + 1), are: x(t) 0.4 -0.5 0.3 1 d(t) = 10:35] x(t + 1) = -0.5 0.2 -0.1 d(t + 1) = [-00255] Activations Y5 4 O = 0 O = 0 U4 15 U1 U2 U3 ub X1 X2 X3 Activations Xb = -1 Answer the following questions: a. [70 marks] Use the delta training rule to calculate the state of the weight matrix at the end of steps t and t + 1. The learning constant n = 0.1. b. [30 marks] Write a MATLAB function to implement the delta training rule. The function should take as inputs: the current weight matrix W, the training example input x, the training example output d, and the learning factor n. For example, to solve the problem above, the inputs should be: W= [0,25 10.25 10.3 -0.15 1 0.42 -0.75 0.5 0.5 X = 0.4 -0.5 0.3 -1 -0.5 0.2 -0.1 -1 0.75 d= 10.35 L0.25 -0.157 Use the function to verify the final answer of your analytical solution. The perceptron shown in the below figure takes real-valued inputs and produces real values according to a sigmoid activation function. At the start of step t in training the weight matrix is: W= 0.5 T0.25 0.3 [0.25 -0.15 1 0.42 -0.75 0.5) The next two input vectors in the training set, x(t) and x(t + 1), and their desired activation vectors d(t) and d(t + 1), are: x(t) 0.4 -0.5 0.3 1 d(t) = 10:35] x(t + 1) = -0.5 0.2 -0.1 d(t + 1) = [-00255] Activations Y5 4 O = 0 O = 0 U4 15 U1 U2 U3 ub X1 X2 X3 Activations Xb = -1 Answer the following questions: a. [70 marks] Use the delta training rule to calculate the state of the weight matrix at the end of steps t and t + 1. The learning constant n = 0.1. b. [30 marks] Write a MATLAB function to implement the delta training rule. The function should take as inputs: the current weight matrix W, the training example input x, the training example output d, and the learning factor n. For example, to solve the problem above, the inputs should be: W= [0,25 10.25 10.3 -0.15 1 0.42 -0.75 0.5 0.5 X = 0.4 -0.5 0.3 -1 -0.5 0.2 -0.1 -1 0.75 d= 10.35 L0.25 -0.157 Use the function to verify the final answer of your analytical solution