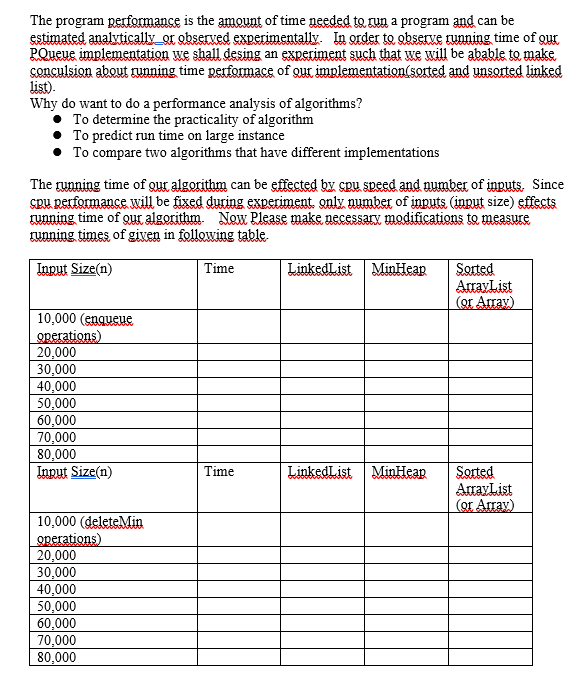
The Priority Queue ADT As an ADT, a priority queue P supports the following functions: - isPQueuempty(): returns true if pqueue is empty otherwise false - size(): Return the number of elements in P. - empty(): Return true if P is empty and false otherwise. - insert(e): Insert a new element e into P. - min( : Return a reference to an element of P with the smallest associated key yalue (but do not remoye it); an error condition occurs if the priority queue is empty. - remoyeMing: Remove from P the element referenced ba mino; an error condition occurs if the prioritx queue is empty. Example: The following table shows a series of operations and their effects on an initially emptx prioritx queue P. Each element consists of an integer, which we assume to be sorted according to the natural ordering of the integers. Note that each call to min returns a reference to an entry in the queue, not the actual value. Although the "Priority Queue" column shows the items in sorted order, the priority queue need not store elements in this order. You may use following interface to implement PriorityQueue public interface PriorityQueu public int peek(); public void insert(int item); public int deletMing; public int size); \} Implementing a Priority Queue with an array In this section, we show how to implement a priority queue by storing its elements in an Linked list. Jle may sonsider two realizations, depending on whether we sort the elements of the list. 1. Implementation with an Unsorted arxay Let us first consider the implementation of a priority queue P by an ynsorted linked list L. A simple wax to perform the operation insert(e) on P is by adding each new element at the begining of L. This implementation of insert takes O(1) time. Since the insertion does not consider key values, the resulting list L is unsorted. As a consequence, in order to perform either of the operations min or remoreMin on P, we must inspect all the entries of the list to find one with the minimum key yalue. Thus: functions min and removeMin take O(n) time each, where n is the number of elements in P at the time the function is executed. 2. Implementation with a Sorted Array An alternative implementation of a priority queue P also yses a list L, except that this time let us store the ellements sorted by their kex yalues. Specifically, wae represent the priority gueue P by using a list L of elements sorted by nondecreasing key yalues. which means that the first element of L has the smallest kex. We can implement function min in this case by accessing the element associated with the first element of the list L. Likewise, we can implement the removeMin function of P by remoying first node of list L. Assuming that L is implemented as a linked lists sperations min and removeMin in P take Q(1) time, so are quite efficient. Following table compares the running times of the functions of a priority queue realized by means of an ynsorted and sorted list respectively. There is an interesting contrast between the two functions. An ynsorted list allows for fast insertions but slow queries and deletions, while a sorted list allews for fast gueries and deletions, but slew insertions. Lab Work Task 1 Implement_Priority Queue using Linked List and perform 100,000 tandom yalue insertions while calculating running time(number of iterations) for each operation and recerd them. Lab Work_Task 2 Implement_Prioritx Queue using_MinHeap, and perform 100,000 random yalue insertions while calculating running time(number of iterations) far each oneration and recerd them. The program performance is the amount of time needed to run a program and can be estimated analytically or observed experimentally. In order te observe running time of our PQueue implementation we shall desing an experiment such that we will be abable to make conculsion about running time performace of our implementation(sorted and ynsorted linked list). Why do want to do a performance analysis of algorithms? - To determine the practicality of algorithm - To predict run time on large instance - To compare two algorithms that have different implementations The running time of our algorithm can be effected by cpu speed and number of inputs. Since cpu performance will be fixed during experiment only number of inputs (inqut size) effects running time of out algorithm. Now Please make necessarx modifications to measure running times of given in following table