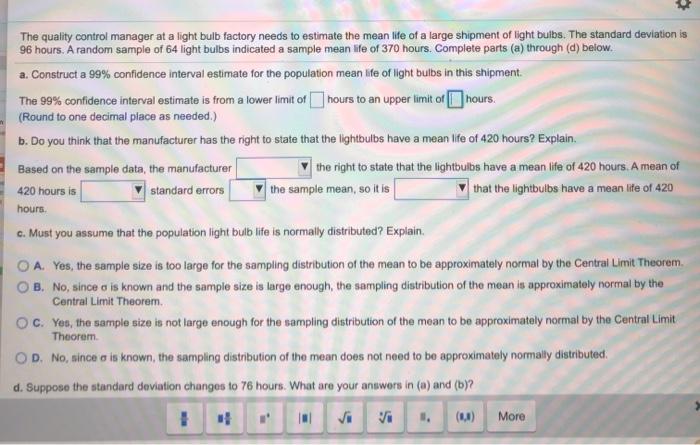
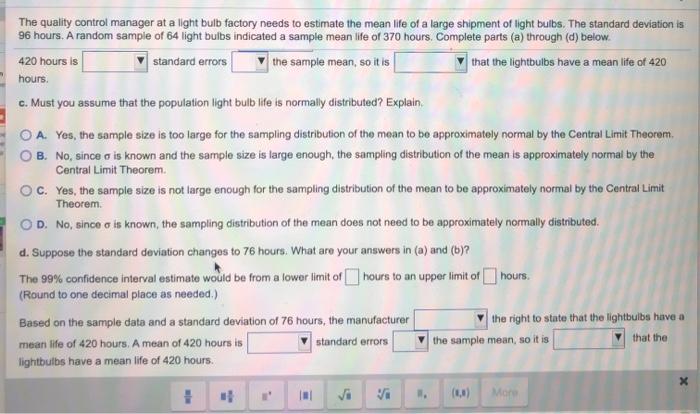
The quality control manager at a light bulb factory needs to estimate the mean life of a large shipment of light bulbs. The standard deviation is 96 hours. A random sample of 64 light bulbs indicated a sample mean life of 370 hours. Complete parts (a) through (d) below. a. Construct a 99% confidence interval estimate for the population mean life of light bulbs in this shipment. The 99% confidence interval estimate is from a lower limit of hours to an upper limit of hours. (Round to one decimal place as needed.) b. Do you think that the manufacturer has the right to state that the lightbulbs have a mean life of 420 hours? Explain. Based on the sample data, the manufacturer the right to state that the lightbulbs have a mean life of 420 hours. A mean of 420 hours is standard errors the sample mean, so it is that the lightbulbs have a mean life of 420 hours c. Must you assume that the population light bulb life is normally distributed? Explain. O A. Yes, the sample size is too large for the sampling distribution of the mean to be approximately normal by the Central Limit Theorem 8. No, since is known and the sample size is large enough the sampling distribution of the mean is approximately normal by the Central Limit Theorem OC. Yes, the sample size is not large enough for the sampling distribution of the mean to be approximately normal by the Central Limit Theorem OD. No, since is known, the sampling distribution of the mean does not need to be approximately normally distributed. d. Suppose the standard deviation changes to 76 hours. What are your answers in (a) and (b)? # More The quality control manager at a light bulb factory needs to estimate the mean life of a large shipment of light bulbs. The standard deviation is 96 hours. A random sample of 64 light bulbs indicated a sample mean life of 370 hours. Complete parts (a) through (d) below. 420 hours is standard errors the sample mean, so it is that the lightbulbs have a mean life of 420 hours. c. Must you assume that the population light bulb life is normally distributed? Explain. O A. Yes, the sample size is too large for the sampling distribution of the mean to be approximately normal by the Central Limit Theorem B. No, since o is known and the sample size is large enough, the sampling distribution of the mean is approximately normal by the Central Limit Theorem OC. Yes, the sample size is not large enough for the sampling distribution of the mean to be approximately normal by the Central Limit Theorem OD. No, since a is known, the sampling distribution of the mean does not need to be approximately normally distributed d. Suppose the standard deviation changes to 76 hours. What are your answers in (a) and (b)? The 99% confidence interval estimate would be from a lower limit of hours to an upper limit of hours (Round to one decimal place as needed.) Based on the sample data and a standard deviation of 76 hours, the manufacturer the right to state that the lightbulbs have a mean life of 420 hours, A mean of 420 hours is standard errors the sample mean, so it is lightbulbs have a mean life of 420 hours. that the X va (1.) MO The quality control manager at a light bulb factory needs to estimate the mean life of a large shipment of light bulbs. The standard deviation is 96 hours. A random sample of 64 light bulbs indicated a sample mean life of 370 hours. Complete parts (a) through (d) below. a. Construct a 99% confidence interval estimate for the population mean life of light bulbs in this shipment. The 99% confidence interval estimate is from a lower limit of hours to an upper limit of hours. (Round to one decimal place as needed.) b. Do you think that the manufacturer has the right to state that the lightbulbs have a mean life of 420 hours? Explain. Based on the sample data, the manufacturer the right to state that the lightbulbs have a mean life of 420 hours. A mean of 420 hours is standard errors the sample mean, so it is that the lightbulbs have a mean life of 420 hours c. Must you assume that the population light bulb life is normally distributed? Explain. O A. Yes, the sample size is too large for the sampling distribution of the mean to be approximately normal by the Central Limit Theorem 8. No, since is known and the sample size is large enough the sampling distribution of the mean is approximately normal by the Central Limit Theorem OC. Yes, the sample size is not large enough for the sampling distribution of the mean to be approximately normal by the Central Limit Theorem OD. No, since is known, the sampling distribution of the mean does not need to be approximately normally distributed. d. Suppose the standard deviation changes to 76 hours. What are your answers in (a) and (b)? # More The quality control manager at a light bulb factory needs to estimate the mean life of a large shipment of light bulbs. The standard deviation is 96 hours. A random sample of 64 light bulbs indicated a sample mean life of 370 hours. Complete parts (a) through (d) below. 420 hours is standard errors the sample mean, so it is that the lightbulbs have a mean life of 420 hours. c. Must you assume that the population light bulb life is normally distributed? Explain. O A. Yes, the sample size is too large for the sampling distribution of the mean to be approximately normal by the Central Limit Theorem B. No, since o is known and the sample size is large enough, the sampling distribution of the mean is approximately normal by the Central Limit Theorem OC. Yes, the sample size is not large enough for the sampling distribution of the mean to be approximately normal by the Central Limit Theorem OD. No, since a is known, the sampling distribution of the mean does not need to be approximately normally distributed d. Suppose the standard deviation changes to 76 hours. What are your answers in (a) and (b)? The 99% confidence interval estimate would be from a lower limit of hours to an upper limit of hours (Round to one decimal place as needed.) Based on the sample data and a standard deviation of 76 hours, the manufacturer the right to state that the lightbulbs have a mean life of 420 hours, A mean of 420 hours is standard errors the sample mean, so it is lightbulbs have a mean life of 420 hours. that the X va (1.) MO