Answered step by step
Verified Expert Solution
Question
1 Approved Answer
The region e enclosed by the curves y=3x and y=x^(2) is rotated about the x -axis. Find the volume of the resulting solid. Solution (1)
The region
eenclosed by the curves
y=3xand
y=x^(2)is rotated about the
x-axis. Find the volume of the resulting solid.\ Solution\ (1)\ A cross-section in the plane
P_(x)has the shape of a washer (an annular ring) with inner radius\ and an outer radius\ , so we find the cross-sectional area by subtracting the area of the inner circle from the area of the outer circle.\ \ Therefore, we have\
V=\\\\int_0^3 A(x)dx=\\\\int_0^3 \\\\pi (9x^(2)-x^(4))dx\ =\\\\pi [|]_(0)^(3)= 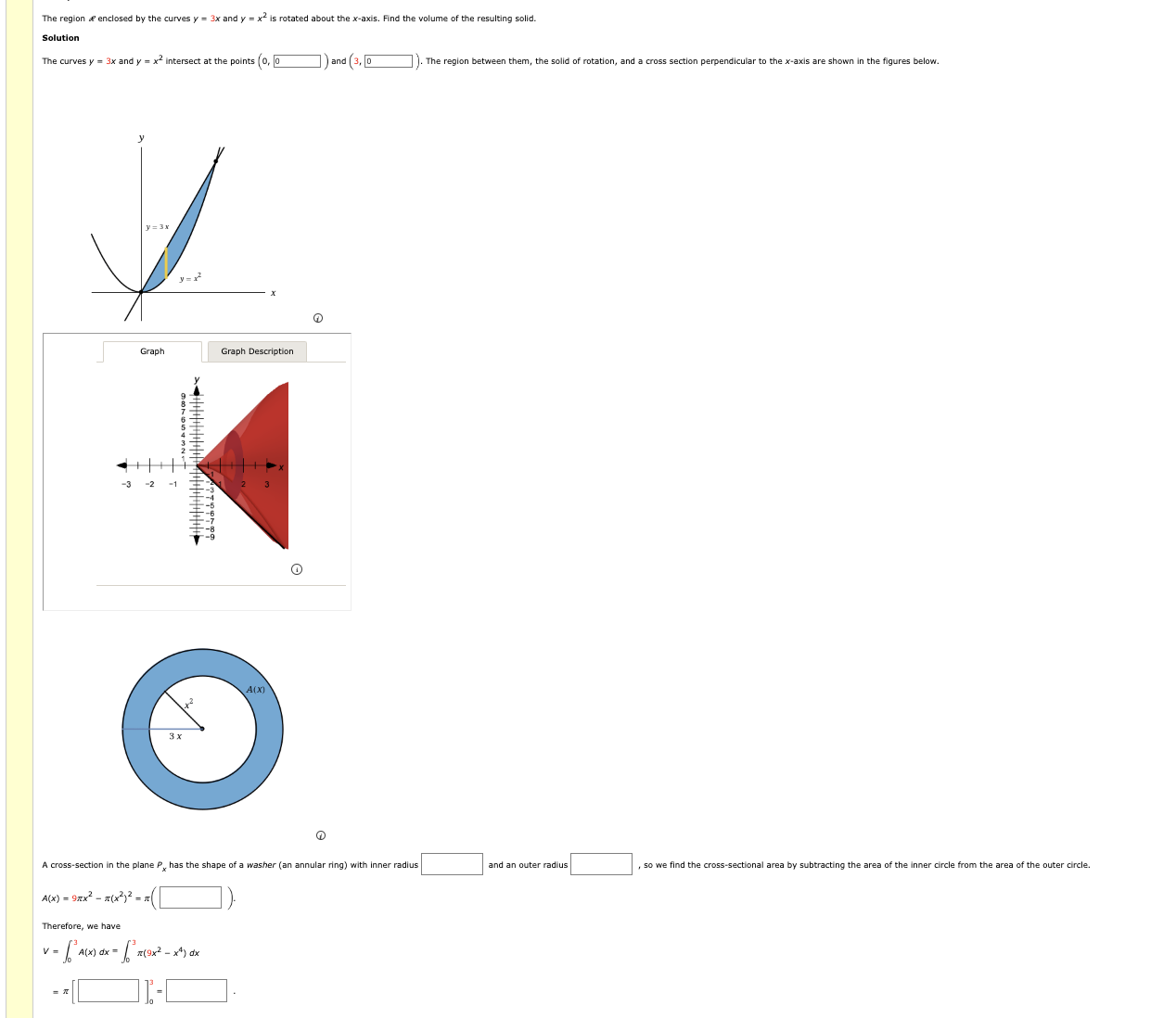
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


