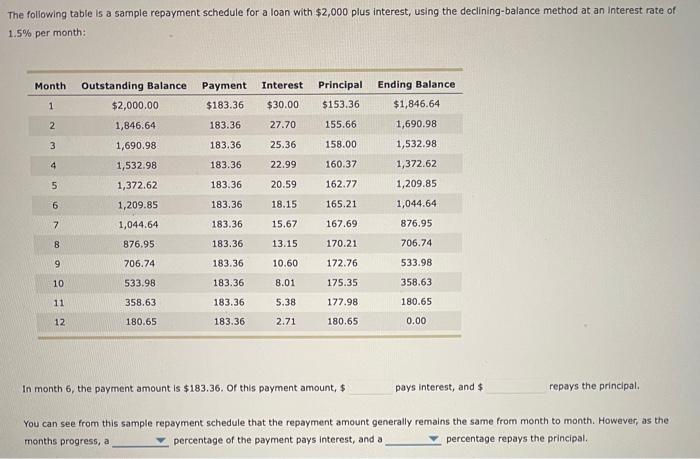
The rule of 78s method (also called the sum of the digits method) is the most widely used method for calculating a prepayment penalty. Its name derives from the fact that for a one-year loan, the numbers between 1 and 12 representing each month add up to 78 (12 + 11 + 10 + 9 + 8 + 7+ 6 + 5+4 + 3 + 2 + 1 - 78) To illustrate the use of the rule of 785 method, consider the following example: Hilary Taylor from New Orleans, Louisiana, has borrowed $1,500 for 12 months plus an additional finance charge of $240. She is scheduled to pay equal monthly installments of $145 ($1,740 / 12). Assume that Hilary wants to pay off the loan after only 3 months Step 1: Each month of Hilary's toan is assigned a value (12 for the first month, 11 for the second month, 10 for the third month, and so on). Hilary has the loan for the first 3 months. Adding up the values for each of the first 3 months gives you the following number: Step 2: According to the rule of 785 method, the lender assumes that a portion of the $240 add- on interest has already been pald. To determine how much interest that Hilary has already pald, divide your answer from step 1 (the sum of the values for each month that Hilary has the loan) by 78. Then multiply this ratio by the total amount of add-on interest ($240). (Note: Round your answer to the nearest cent.) / 78) * $240 $ Interest Paid Step 3: After 3 months, Hilary has made a total of $435 in payments. Subtract the total amount of interest paid (from step 2) from $435. This gives you the amount of the $1,500 originally borrowed that has been repaid. Perform this calculation to determine how much of the original loan (the principal) has been repaid: (Note: Round your answer to the nearest cent.) $435 (Total Payments Made) - $ (Interest Paid) = $ (Amount of Original $1,500 Borrowed That Has Been Repaid) Step 4: Determine how much of the original amount borrowed remains unpaid. Subtract the amount of the principal that has been repaid (from step 3) from the original amount borrowed: (Note: Round your answer to the nearest cent.) $1,500 (Original Amount Borrowed) - $ (Amount of Principal Repaid) = $ (Principal Left Unpaid) Step 5: Hilary pays off her loan after only 3 months, which is one-quarter (3/12 = 1/4) of the way through the loan. Hilary might (incorrectly) expect to owe only $1,125 of the original amount borrowed (the remaining three-quarters of the original amount borrowed). (Note: Round your answer to the nearest cent.) However, in reality, Hilary still owes $ of the original amount borrowed (from step 4). Now you can calculate the prepayment penalty as follows: $ (Amount of Original Loan Unpaid) - $1,125 = $ (Prepayment Penalty) $ The following table is a sample repayment schedule for a loan with $2,000 plus interest, using the declining-balance method at an interest rate of 1.5% per month: Month Interest Principal Outstanding Balance $2,000.00 Payment $183.36 1 $30.00 $153.36 2 1,846.64 183.36 27.70 155.66 3 1,690.98 183.36 25.36 158.00 Ending Balance $1,846.64 1,690.98 1,532.98 1,372.62 1,209.85 1,044.64 876.95 4 183.36 22.99 160.37 1,532.98 1,372.62 5 183.36 20.59 162.77 6 1,209.85 183.36 18.15 165.21 7 1,044.64 183.36 15.67 167.69 876.95 183.36 13.15 170.21 706.74 9 706.74 172.76 533.98 183.36 183.36 10.60 8.01 10 533.98 175.35 358.63 11 358.63 183.36 177.98 180.65 5.38 2.71 12 180.65 183.36 180.65 0.00 In month 6, the payment amount is $183.36. of this payment amount, $ pays Interest, and $ repays the principal. You can see from this sample repayment schedule that the repayment amount generally remains the same from month to month. However, as the months progress, a percentage of the payment pays Interest, and a percentage repays the principal