***The sampling code is: (THIS IS THE ONE YOU NEED TO MODIFY TO ANSWER THE ABOVE QUESTION)

% % ECE3614 Introduction to Communications % % Matlab Assignment 3: Sampling % % This example demonstrates decimation and interpolation of an % input audio signal. The signal is read from a file 'matlab3.dat' % with a sampling rate of 16 kHz and then decimated down to % just 2 kHz. The signal is then interpolated to 16 kHz and the % resulting audio signal and spectrum is plotted. %

clear all; close all;

% load audio signal vector m = load('audio.dat'); m = m(:)'; % ensure m is a column vector n1 = length(m); % number of input audio samples fs1 = 16000; % input audio sampling frequency (samples/second) fs2 = 2000; % sampling rate

% only certain values of fs2 will work well if fs2 ~=500 && fs2 ~= 1000 && fs2~=2000 && fs2 ~= 4000 && fs2 ~= 8000, error('please choose fs2 to be 500, 1000, 2000, 4000, or 8000'); end;

% compute decimation D = fs1 / fs2; % decimation rate n2 = n1 / D; % number of output audio samples

% set up time vectors t1 =[0:(n1-1)]/fs1; % input signal time vector t2 =[0:(n2-1)]/fs2; % decimated signal time vector

% DECIMATOR % input : m(t), input audio message signal % output : ms(t), output message signal with reduce sample rate

% TODO: apply low-pass filter to 'm' and store into 'mfilt' mfilt = zeros(1,n1);

% TODO: down-sample 'mfilt' and store into 'ms' (keep every D^th sample) ms = zeros(1,n2);

% INTERPOLATOR % input : ms(t), sampled audio message signal % output : y(t), interpolated audio message signal

% TODO: up-sample 'ms' (pad with zeros) and store into 'v' % v = [ms(1) 0 0 0 ... ms(2) 0 0 0 ... ms(3) 0 0 0 ...] v = zeros(1,n1);

% TODO: filter out resulting images and scale by decimation rate y = zeros(1,n1);

% % PLOT RESULTS %

% plot time-domain signals figure; subplot(4,1,1), plot(t1,m); ylabel('m(t)'); axis([0 t1(end) -1 1]); grid on; subplot(4,1,2), plot(t2,ms); ylabel('m_s(t)'); axis([0 t1(end) -1 1]); grid on; subplot(4,1,3), plot(t1,v); ylabel('v(t)'); axis([0 t1(end) -1 1]); grid on; subplot(4,1,4), plot(t1,y); ylabel('y(t)'); axis([0 t1(end) -1 1]); grid on; xlabel('Time (s)');

% spectrum plots % NOTE: this is an approximation to the Fourier transform of the signals nfft = 8192; % Discrete fourier transform size f1 = [[0:(nfft-1)]fft - 0.5]*fs1; % frequency vector (32 kHz) f2 = [[0:(nfft-1)]fft - 0.5]*fs2; % frequency vector (sub-sampled) w1 = hamming(n1)'; % spectral shaping window w2 = hamming(n2)'; % g1 = 1 / ( mean(w1) * n1 ); % scaling factors g2 = 1 / ( mean(w2) * n2 ); % % compute approximate PSD of signals m, ms, v, and y M = abs(fftshift(fft(m .*w1, nfft))) * g1; % M(f) original audio spectrum MS = abs(fftshift(fft(ms.*w2, nfft))) * g2; % Ms(f) sampled audio spectrum V = abs(fftshift(fft(v .*w1, nfft))) * g1 * D; % V(f) up-sampled spectrum Y = abs(fftshift(fft(y .*w1, nfft))) * g1; % Y(f) reconstructed audio spectrum

% plot frequency-domain signals figure; fmin = -4000; fmax = 4000; subplot(4,1,1), plot(f1, M, 'LineWidth',2); axis([fmin fmax 0 0.5]); ylabel('M(f)'); grid on; subplot(4,1,2), plot(f2, MS,'LineWidth',2); axis([fmin fmax 0 0.5]); ylabel('M_s(f)'); grid on; subplot(4,1,3), plot(f1, V, 'LineWidth',2); axis([fmin fmax 0 0.5]); ylabel('V(f)'); grid on; subplot(4,1,4), plot(f1, Y, 'LineWidth',2); axis([fmin fmax 0 0.5]); ylabel('Y(f)'); grid on; xlabel('Frequency (Hz)');

***THE AUDIO DATA CONTAINING THE AUDIO SIGNAL IS

0.00000000 0.00003255 0.00012051 0.00025021 0.00040984 0.00059041 0.00078640 0.00099620 0.00122224 0.00147085 0.00175189 0.00207814 0.00246451 0.00292715 0.00348235 0.00414548 0.00492986 0.00584564 0.00689890 0.00809081 0.00941703 0.01086732 0.01242529 0.01406836 0.01576763 0.01748779 0.01918688 0.02081579 0.02231751 0.02362625 0.02466621 0.02535047 0.02558007 0.02524370 0.02421855 0.02237301 0.01957207 0.01568592 0.01060221 0.00424136 -0.00342689 -0.01236873 -0.02247762 -0.03357533 -0.04542493 -0.05775420 -0.07028506 -0.08276229 -0.09497564 -0.10677185 -0.11805620 -0.12878604 -0.13895959 -0.14860346 -0.15776093 -0.16648247 -0.17481865 -0.18281530 -0.19051028 -0.19793155 -0.20509571 -0.21200680 -0.21865489 -0.22501410 -0.23103979 -0.23666461 -0.24179304 -0.24629416 -0.24999222 -0.25265515 -0.25398107 -0.25358413 -0.25098211 -0.24559062 -0.23673148 -0.22366564 -0.20566199 -0.18210891 -0.15266258 -0.11740408 -0.07695431 -0.03248805 0.01438722 0.06186909 0.10824172 0.15211090 0.19253088 0.22901391 0.26145517 0.29002018 0.31503283 0.33688519 0.35597500 0.37266790 0.38727808 0.40006102 0.41121322 0.42087550 0.42913766 0.43604352 0.44159570 0.44576036 0.44847201 0.44963897 0.44915004 0.44688299 0.44271533 0.43653765 0.42826928 0.41787548 0.40538483 0.39090448 0.37463106 0.35685493 0.33795600 0.31839087 0.29867231 0.27934337 0.26094923 0.24401020 0.22899815 0.21631820 0.20629604 0.19917027 0.19508893 0.19410900 0.19619790 0.20123663 0.20902422 0.21928385 0.23167090 0.24578302 0.26117234 0.27735898 0.29384529 0.31012919 0.32571574 0.34012532 0.35289805 0.36359379 0.37178819 0.37706525 0.37900764 0.37718596 0.37114892 0.36041628 0.34447728 0.32279764 0.29483884 0.26009346 0.21813976 0.16871630 0.11181245 0.04776410 -0.02266538 -0.09824449 -0.17729927 -0.25781991 -0.33764154 -0.41466733 -0.48708504 -0.55352845 -0.61315370 -0.66562772 -0.71104909 -0.74983307 -0.78259078 -0.81002371 -0.83284337 -0.85171762 -0.86723965 -0.87991379 -0.89015237 -0.89827863 -0.90453231 -0.90907519 -0.91199519 -0.91330777 -0.91295394 -0.91079432 -0.90659868 -0.90003066 -0.89062762 -0.87777631 -0.86068648 -0.83836721 -0.80961448 -0.77302425 -0.72705139 -0.67013892 -0.60093855 -0.51862399 -0.42325867 -0.31614483 -0.19992237 -0.07840960 0.04383860 0.16222533 0.27280478 0.37276017 0.46056365 0.53585205 0.59913614 0.65146811 0.69415239 0.72853559 0.75587614 0.77727710 0.79366194 0.80577582 0.81419989 0.81937091 0.82160161 0.82109999 0.81798673 0.81231135 0.80406745 0.79320844 0.77966432 0.76336052 0.74423906 0.72228182 0.69753471 0.67013094 0.64031048 0.60843263 0.57497872 0.54054304 0.50581179 0.47153162 0.43847153 0.40738254 0.37895970 0.35381043 0.33243098 0.31519177 0.30233070 0.29395269 0.29003370 0.29042777 0.29487593 0.30301700 0.31439998 0.32849862 0.34472810 0.36246376 0.38106080 0.39987395 0.41827528 0.43566856 0.45149890 0.46525667 0.47647575 0.48472639 0.48960382 0.49071396 0.48765779 0.48001635 0.46733831 0.44913271 0.42487000 0.39399506 0.35595685 0.31025891 0.25653381 0.19464051 0.12477680 0.04758879 -0.03575064 -0.12352790 -0.21356710 -0.30340759 -0.39055643 -0.47276228 -0.54824607 -0.61583762 -0.67499952 -0.72575409 -0.76855057 -0.80411356 -0.83330445 -0.85701292 -0.87608299 -0.89126972 -0.90321931 -0.91246466 -0.91942988 -0.92443880 -0.92772421 -0.92943560 -0.92964434 -0.92834524 -0.92545412 -0.92080091 -0.91411787 -0.90502282 -0.89299774 -0.87736394 -0.85725699 -0.83160770 -0.79913990 -0.75840145 -0.70785074 -0.64602127 -0.57177801 -0.48465091 -0.38518449 -0.27519125 -0.15777588 -0.03704469 0.08246765 0.19649132 0.30161472 0.39561393 0.47748041 0.54722159 0.60555556 0.65360458 0.69264784 0.72395175 0.74867034 0.76779796 0.78215609 0.79239959 0.79903256 0.80242771 0.80284617 0.80045628 0.79535146 0.78756728 0.77709890 0.76391929 0.74799907 0.72932807 0.70793812 0.68392592 0.65747395 0.62886695 0.59850096 0.56688271 0.53461801 0.50238944 0.47092525 0.44096317 0.41321309 0.38832273 0.36684918 0.34923817 0.33581099 0.32675833 0.32213972 0.32188692 0.32581041 0.33360839 0.34487808 0.35912980 0.37580376 0.39428945 0.41394704 0.43412924 0.45420212 0.47356285 0.49165274 0.50796435 0.52204219 0.53347733 0.54189667 0.54694819 0.54828357 0.54553983 0.53832157 0.52618555 0.50863008 0.48509203 0.45495561 0.41757795 0.37233744 0.31870976 0.25637372 0.18534145 0.10609617 0.01970662 -0.07212318 -0.16710881 -0.26256374 -0.35568220 -0.44386662 -0.52501862 -0.59772369 -0.66129878 -0.71571733 -0.76145644 -0.79931820 -0.83026532 -0.85529327 -0.87534406 -0.89125713 -0.90374781 -0.91340385 -0.92069216 -0.92596987 -0.92949608 -0.93144190 -0.93189752 -0.93087563 -0.92831054 -0.92405289 -0.91785944 -0.90937814 -0.89812848 -0.88347843 -0.86462080 -0.84055439 -0.81007949 -0.77182258 -0.72430980 -0.66611058 -0.59606542 -0.51358885 -0.41899860 -0.31377503 -0.20062985 -0.08329442 0.03396557 0.14698233 0.25226992 0.34739408 0.43106613 0.50300748 0.56368800 0.61403942 0.65520947 0.68838338 0.71467192 0.73505228 0.75034542 0.76121569 0.76818248 0.77163757 0.77186434 0.76905733 0.76334152 0.75479164 0.74345188 0.72935649 0.71255120 0.69311543 0.67118383 0.64696583 0.62076085 0.59296683 0.56408008 0.53468536 0.50543639 0.47702834 0.45016543 0.42552699 0.40373553 0.38532958 0.37074274 0.36028955 0.35415743 0.35240382 0.35495759 0.36162385 0.37209200 0.38594715 0.40268509 0.42173100 0.44246137 0.46422816 0.48638343 0.50830233 0.52940230 0.54915646 0.56710031 0.58283119 0.59600115 0.60630426 0.61345980 0.61719278 0.61721319 0.61319510 0.60475701 0.59144477 0.57271908 0.54795100 0.51642970 0.47738923 0.43006182 0.37376555 0.30803056 0.23275932 0.14840114 0.05610145 -0.04222888 -0.14397833 -0.24605906 -0.34526326 -0.43866862 -0.52398477 -0.59975393 -0.66537624 -0.72098975 -0.76726908 -0.80520838 -0.83593420 -0.86056866 -0.88014401 -0.89555906 -0.90756490 -0.91676823 -0.92364359 -0.92854855 -0.93173828 -0.93337738 -0.93354805 -0.93225408 -0.92942031 -0.92488744 -0.91840223 -0.90960294 -0.89800089 -0.88295934 -0.86367326 -0.83915566 -0.80824043 -0.76961598 -0.72190764 -0.66382622 -0.59439055 -0.51320821 -0.42076213 -0.31861338 -0.20941872 -0.09669979 0.01561144 0.12373026 0.22451447 0.31576687 0.39630344 0.46583119 0.52472217 0.57376670 0.61395990 0.64634408 0.67190739 0.69152808 0.70595125 0.71578623 0.72151601 0.72351300 0.72205797 0.71736032 0.70957909 0.69884462 0.68528054 0.66902591 0.65025667 0.62920514 0.60617592 0.58155621 0.55581882 0.52951664 0.50326842 0.47773688 0.45360121 0.43152683 0.41213553 0.39597839 0.38351346 0.37508876 0.37093089 0.37113834 0.37567917 0.38439258 0.39699427 0.41308604 0.43217013 0.45366831 0.47694571 0.50133792 0.52617955 0.55083158 0.57470476 0.59727676 0.61810154 0.63681048 0.65310592 0.66674833 0.67753894 0.68529936 0.68984974 0.69098642 0.68845981 0.68195294 0.67106133 0.65527531 0.63396701 0.60638589 0.57166900 0.52887493 0.47705249 0.41535527 0.34320807 0.26051755 0.16789626 0.06684082 -0.04021432 -0.15003571 -0.25893790 -0.36327248 -0.45992575 -0.54668212 -0.62236820 -0.68678068 -0.74046892 -0.78446454 -0.82003132 -0.84847438 -0.87101680 -0.88873407 -0.90252974 -0.91313650 -0.92113051 -0.92695053 -0.93091699 -0.93324831 -0.93407312 -0.93343802 -0.93131054 -0.92757751 -0.92203886 -0.91439702 -0.90424253 -0.89103710 -0.87409670 -0.85257894 -0.82548253 -0.79166926 -0.74992259 -0.69905715 -0.63808783 -0.56645216 -0.48425386 -0.39246589 -0.29301373 -0.18867365 -0.08277472 0.02123257 0.12022266 0.21173630 0.29414672 0.36665011 0.42913119 0.48197135 0.52585575 0.56161261 0.59009671 0.61211520 0.62838734 0.63952876 0.64605179 0.64837597 0.64684437 0.64174344 0.63332460 0.62182662 0.60749782 0.59061685 0.57151075 0.55056873 0.52824998 0.50508425 0.48166461 0.45863257 0.43665697 0.41640849 0.39853257 0.38362289 0.37219762 0.36467948 0.36138013 0.36248866 0.36806405 0.37803112 0.39218044 0.41017266 0.43154838 0.45574419 0.48211559 0.50996577 0.53857872 0.56725359 0.59533668 0.62224769 0.64749735 0.67069521 0.69154751 0.70984668 0.72545452 0.73828132 0.74826332 0.75533969 0.75943010 0.76041312 0.75810521 0.75223999 0.74244757 0.72823433 0.70896451 0.68384688 0.65193257 0.61213349 0.56327524 0.50420077 0.43393971 0.35194693 0.25838855 0.15441502 0.04232242 -0.07450576 -0.19193577 -0.30565337 -0.41180880 -0.50753608 -0.59120408 -0.66237681 -0.72156590 -0.76989855 -0.80880367 -0.83977178 -0.86420116 -0.88331757 -0.89814576 -0.90951235 -0.91806432 -0.92429297 -0.92855748 -0.93110500 -0.93208602 -0.93156466 -0.92952398 -0.92586651 -0.92041049 -0.91288216 -0.90290498 -0.88998741 -0.87351155 -0.85272715 -0.82675728 -0.79462444 -0.75530743 -0.70783854 -0.65144473 -0.58572443 -0.51083258 -0.42762784 -0.33772636 -0.24341960 -0.14745099 -0.05269564 0.03817669 0.12297205 0.20012313 0.26871248 0.32839660 0.37927559 0.42174962 0.45639040 0.48384137 0.50474896 0.51972169 0.52931092 0.53400750 0.53424909 0.53043440 0.52294133 0.51214669 0.49844553 0.48226816 0.46409321 0.44445504 0.42394448 0.40320244 0.38290672 0.36375331 0.34643396 0.33161226 0.31990013 0.31183640 0.30786808 0.30833462 0.31345489 0.32331643 0.33786711 0.35690988 0.38010177 0.40695925 0.43687182 0.46912511 0.50293352 0.53748048 0.57196258 0.60563247 0.63783531 0.66803430 0.69582300 0.72092430 0.74317794 0.76251985 0.77895688 0.79254012 0.80333914 0.81141842 0.81681636 0.81952633 0.81947905 0.81652510 0.81041654 0.80078689 0.78712930 0.76877401 0.74486809 0.71436369 0.67602553 0.62847403 0.57028564 0.50017308 0.41725763 0.32141705 0.21364196 0.09627783 -0.02699441 -0.15153184 -0.27241191 -0.38522386 -0.48670601 -0.57504355 -0.64980450 -0.71162764 -0.76182157 -0.80199958 -0.83381117 -0.85877823 -0.87821561 -0.89320856 -0.90462231 -0.91312664 -0.91922449 -0.92327880 -0.92553487 -0.92613719 -0.92514084 -0.92251773 -0.91815845 -0.91187015 -0.90337173 -0.89228746 -0.87814121 -0.86035433 -0.83825166 -0.81108133 -0.77805508 -0.73841490 -0.69152873 -0.63701093 -0.57485224 -0.50553315 -0.43008659 -0.35007998 -0.26750361 -0.18457967 -0.10353205 -0.02636892 0.04527732 0.11023022 0.16777192 0.21758846 0.25968443 0.29429078 0.32178219 0.34261219 0.35726848 0.36624662 0.37003876 0.36913359 0.36402362 0.35521641 0.34324669 0.32868685 0.31215362 0.29430948 0.27585802 0.25753350 0.24008536 0.22425960 0.21077849 0.20032077 0.19350323 0.19086437 0.19284975 0.19979833 0.21192890 0.22932585 0.25192483 0.27949946 0.31165203 0.34781190 0.38724572 0.42908266 0.47235545 0.51605518 0.55919370 0.60086550 0.64030003 0.67689715 0.71024210 0.74010025 0.76639557 0.78917845 0.80858911 0.82482155 0.83809130 0.84860859 0.85655705 0.86207697 0.86525176 0.86609597 0.86454313 0.86043203 0.85349010 0.84331303 0.82934057 0.81082967 0.78682849 0.75615862 0.71741865 0.66902948 0.60934887 0.53688402 0.45061776 0.35042465 0.23748760 0.11455520 -0.01413870 -0.14338362 -0.26783272 -0.38290016 -0.48540568 -0.57379353 -0.64795694 -0.70883410 -0.75795843 -0.79708354 -0.82792793 -0.85203210 -0.87069880 -0.88498491 -0.89572032 -0.90353749 -0.90890222 -0.91214109 -0.91346335 -0.91297732 -0.91070136 -0.90657043 -0.90043913 -0.89208252 -0.88119634 -0.86739857 -0.85023520 -0.82919356 -0.80372685 -0.77329365 -0.73741425 -0.69574294 -0.64815008 -0.59480183 -0.53622055 -0.47330728 -0.40731280 -0.33975457 -0.27229153 -0.20658001 -0.14413885 -0.08624699 -0.03388569 0.01227477 0.05185345 0.08471604 0.11092428 0.13068793 0.14432513 0.15223377 0.15487356 0.15275686 0.14644554 0.13655082 0.12373330 0.10870089 0.09220317 0.07502159 0.05795593 0.04180827 0.02736607 0.01538619 0.00658106 0.00160754 0.00105821 0.00545363 0.01523381 0.03074671 0.05223176 0.07979743 0.11339340 0.15277999 0.19750007 0.24686107 0.29993566 0.35558886 0.41253495 0.46942122 0.52492801 0.57786885 0.62727336 0.67243932 0.71294816 0.74864638 0.77960197 0.80604768 0.82832204 0.84681619 0.86193079 0.87404414 0.88349045 0.89054600 0.89542064 0.89825210 0.89910093 0.89794435 0.89466729 0.88904957 0.88074818 0.86927410 0.85396418 0.83395020 0.80813032 0.77515341 0.73343400 0.68122432 0.61677641 0.53862334 0.44598164 0.33921875 0.22024752 0.09265117 -0.03862399 -0.16800954 -0.29027344 -0.40135639 -0.49881797 -0.58183021 -0.65084596 -0.70713961 -0.75237953 -0.78831077 -0.81656007 -0.83853956 -0.85541653 -0.86812075 -0.87736924 -0.88369624 -0.88748191 -0.88897676 -0.88832109 -0.88555974 -0.88065304 -0.87348540 -0.86387285 -0.85157161 -0.83628963 -0.81770323 -0.79548110 -0.76931695 -0.73897093 -0.70431792 -0.66539760 -0.62245898 -0.57598983 -0.52672223 -0.47560851 -0.42376791 -0.37241074 -0.32275215 -0.27592954 -0.23293553 -0.19457365 -0.16143781 -0.13391214 -0.11218494 -0.09627000 -0.08602963 -0.08119586 -0.08138797 -0.08612659 -0.09484543 -0.10690241 -0.12159180 -0.13815840 -0.15581418 -0.17375643 -0.19118633 -0.20732572 -0.22143055 -0.23279947 -0.24077727 -0.24475346 -0.24415770 -0.23845419 -0.22713812 -0.20973746 -0.18582370 -0.15503482 -0.11711291 -0.07195675 -0.01968638 0.03928844 0.10420974 0.17394113 0.24698503 0.32155980 0.39573549 0.46760910 0.53548529 0.59802452 0.65432971 0.70396094 0.74688750 0.78339926 0.81400262 0.83932179 0.86001789 0.87673027 0.89003915 0.90044507 0.90836043 0.91410815 0.91792377 0.91995827 0.92027932 0.91886977 0.91562209 0.91032794 0.90266222 0.89216117 0.87819496 0.85993678 0.83633318 0.80608518 0.76765665 0.71933464 0.65937280 0.58624651 0.49902525 0.39781589 0.28415600 0.16117833 0.03338762 -0.09397405 -0.21580077 -0.32793493 -0.42765672 -0.51376203 -0.58631695 -0.64625925 -0.69499878 -0.73410237 -0.76508627 -0.78930236 -0.80789104 -0.82177501 -0.83167437 -0.83813048 -0.84153150 -0.84213617 -0.84009472 -0.83546707 -0.82823934 -0.81833996 -0.80565683 -0.79005698 -0.77140977 -0.74961407 -0.72462878 -0.69650494 -0.66541585 -0.63168089 -0.59577812 -0.55834149 -0.52014076 -0.48204512 -0.44497461 -0.40984598 -0.37752003 -0.34875672 -0.32418185 -0.30426655 -0.28931824 -0.27948072 -0.27474012 -0.27493460 -0.27976603 -0.28881338 -0.30154790 -0.31735092 -0.33553453 -0.35536496 -0.37608773 -0.39695252 -0.41723570 -0.43625801 -0.45339557 -0.46808329 -0.47981057 -0.48811033 -0.49254273 -0.49267596 -0.48806605 -0.47823850 -0.46267452 -0.44080552 -0.41202030 -0.37569041 -0.33121983 -0.27812394 -0.21613940 -0.14535822 -0.06636706 0.01964212 0.11083378 0.20480322 0.29877892 0.38992633 0.47568511 0.55405386 0.62375446 0.68425247 0.73565706 0.77855146 0.81380740 0.84242220 0.86539712 0.88365921 0.89801952 0.90915744 0.91762122 0.92383685 0.92811984 0.93068650 0.93166268 0.93108864 0.92891947 0.92502055 0.91915766 0.91098158 0.90000747 0.88559006 0.86689773 0.84289124 0.81231775 0.77373651 0.72559838 0.66640354 0.59495249 0.51067926 0.41400813 0.30662254 0.19151018 0.07269287 -0.04533357 -0.15829015 -0.26271539 -0.35630768 -0.43796662 -0.50760492 -0.56585081 -0.61374570 -0.65249841 -0.68331496 -0.70729764 -0.72539609 -0.73839282 -0.74690883 -0.75141979 -0.75227696 -0.74972988 -0.74394958 -0.73505221 -0.72312334 -0.70824303 -0.69051173 -0.67007598 -0.64715245 -0.62204804 -0.59517320 -0.56704612 -0.53828575 -0.50959351 -0.48172500 -0.45545467 -0.43153747 -0.41067173 -0.39346659 -0.38041603 -0.37188047 -0.36807519 -0.36906490 -0.37476329 -0.38493708 -0.39921469 -0.41709998 -0.43799165 -0.46120845 -0.48601933 -0.51167672 -0.53744989 -0.56265512 -0.58667935 -0.60899489 -0.62916422 -0.64683508 -0.66172737 -0.67361381 -0.68229662 -0.68758215 -0.68925468 -0.68705064 -0.68063355 -0.66957062 -0.65331237 -0.63117773 -0.60234944 -0.56588730 -0.52077011 -0.46597982 -0.40064064 -0.32421859 -0.23676791 -0.13918057 -0.03336087 0.07776962 0.19050502 0.30081604 0.40492809 0.49984387 0.58365925 0.65561349 0.71591850 0.76547048 0.80554705 0.83755685 0.86286676 0.88270276 0.89810660 0.90992855 0.91883996 0.92535402 0.92984799 0.93258276 0.93371813 0.93332298 0.93138014 0.92778611 0.92234572 0.91476221 0.90462331 0.89138494 0.87435537 0.85268479 0.82536837 0.79127426 0.74921045 0.69804409 0.63687933 0.56528260 0.48351726 0.39272214 0.29495701 0.19306101 0.09032933 -0.00991584 -0.10474116 -0.19189736 -0.26994153 -0.33819941 -0.39662197 -0.44559998 -0.48578548 -0.51794755 -0.54287026 -0.56128993 -0.57386331 -0.58115822 -0.58365907 -0.58178197 -0.57589558 -0.56634496 -0.55347645 -0.53766152 -0.51931781 -0.49892512 -0.47703461 -0.45426960 -0.43131741 -0.40891263 -0.38781351 -0.36877390 -0.35251362 -0.33968999 -0.33087224 -0.32652000 -0.32696589 -0.33240165 -0.34286768 -0.35824578 -0.37825613 -0.40246026 -0.43027193 -0.46097810 -0.49377052 -0.52778701 -0.56215893 -0.59605973 -0.62874843 -0.65960250 -0.68813670 -0.71400651 -0.73699809 -0.75700767 -0.77401469 -0.78805251 -0.79917940 -0.80745175 -0.81289999 -0.81550680 -0.81518684 -0.81176670 -0.80496387 -0.79436411 -0.77939708 -0.75931196 -0.73315715 -0.69977233 -0.65780670 -0.60578377 -0.54223831 -0.46594830 -0.37626669 -0.27351475 -0.15933553 -0.03685082 0.08952883 0.21468387 0.33361785 0.44226514 0.53800506 0.61976599 0.68778604 0.74319951 0.78761271 0.82276751 0.85032199 0.87173461 0.88822168 0.90075878 0.91010392 0.91682805 0.92134515 0.92393776 0.92477675 0.92393496 0.92139524 0.91705349 0.91071761 0.90210347 0.89082952 0.87641243 0.85826717 0.83571638 0.80801513 0.77439756 0.73415086 0.68671744 0.63181844 0.56958004 0.50063387 0.42615786 0.34783163 0.26770133 0.18797650 0.11080370 0.03806739 -0.02874397 -0.08859268 -0.14087597 -0.18536265 -0.22210786 -0.25136732 -0.27352421 -0.28903500 -0.29839465 -0.30211892 -0.30073977 -0.29480983 -0.28491154 -0.27166747 -0.25574846 -0.23787710 -0.21882512 -0.19940404 -0.18044997 -0.16280404 -0.14729075 -0.13469656 -0.12575027 -0.12110605 -0.12132888 -0.12688105 -0.13810805 -0.15522229 -0.17828378 -0.20717845 -0.24159685 -0.28101806 -0.32470525 -0.37171960 -0.42095735 -0.47121069 -0.52124736 -0.56989836 -0.61613956 -0.65915421 -0.69836694 -0.73344716 -0.76428580 -0.79095384 -0.81365230 -0.83266211 -0.84829973 -0.86088118 -0.87069515 -0.87798364 -0.88292839 -0.88564054 -0.88615148 -0.88440276 -0.88023337 -0.87336300 -0.86337022 -0.84966550 -0.83146009 -0.80773479 -0.77721686 -0.73838028 -0.68949377 -0.62874937 -0.55450663 -0.46566966 -0.36216515 -0.24540696 -0.11855113 0.01366286 0.14556057 0.27151282 0.38690181 0.48873467 0.57576340 0.64820135 0.70724578 0.75460007 0.79210386 0.82149831 0.84430597 0.86178922 0.87495434 0.88457729 0.89123637 0.89534379 0.89717266 0.89687816 0.89451325 0.89003983 0.88333672 0.87420602 0.86237991 0.84753031 0.82928391 0.80724540 0.78103139 0.75031579 0.71488554 0.67470177 0.62995765 0.58112114 0.52895050 0.47447353 0.41892893 0.36367712 0.31009569 0.25947776 0.21294947 0.17141623 0.13553956 0.10573954 0.08221469 0.06497016 0.05384704 0.04854820 0.04865858 0.05366040 0.06294472 0.07582201 0.09153364 0.10926616 0.12816864 0.14737262 0.16601278 0.18324632 0.19826851 0.21032303 0.21870631 0.22276648 0.22189882 0.21554032 0.20316716 0.18429878 0.15851279 0.12547410 0.08498041 0.03702314 -0.01814147 -0.07992268 -0.14734444 -0.21903491 -0.29327473 -0.36811154 -0.44152970 -0.51164527 -0.57688472 -0.63610933 -0.68866421 -0.73435283 -0.77335675 -0.80612788 -0.83327882 -0.85548858 -0.87343152 -0.88773027 -0.89892863 -0.90747919 -0.91374010 -0.91797667 -0.92036432 -0.92099041 -0.91985330 -0.91685730 -0.91180247 -0.90436858 -0.89409271 -0.88034085 -0.86227557 -0.83882450 -0.80865987 -0.77020618 -0.72170258 -0.66135315 -0.58759563 -0.49949386 -0.39720254 -0.28237250 -0.15830462 -0.02968865 0.09808518 0.21984364 0.33145488 0.43029588 0.51529020 0.58662511 0.64533042 0.69287211 0.73084093 0.76075299 0.78394427 0.80153019 0.81440383 0.82325384 0.82858983 0.83076894 0.83002045 0.82646792 0.82014918 0.81103555 0.79905166 0.78409737 0.76607295 0.74490789 0.72059274 0.69321205 0.66297480 0.63023778 0.59551698 0.55948301 0.52293868 0.48678033 0.45194736 0.41936679 0.38990006 0.36429820 0.34316883 0.32695577 0.31593005 0.31018937 0.30966373 0.31412479 0.32319834 0.33637972 0.35305273 0.37248788 0.39388859 0.41644846 0.43936065 0.46184775 0.48318636 0.50272375 0.51988510 0.53417100 0.54514628 0.55242182 0.55563190 0.55440918 0.54835992 0.53704175 0.51994678 0.49649378 0.46603437 0.42787992 0.38135713 0.32590002 0.26118174 0.18727984 0.10485144 0.01527362 -0.07931078 -0.17609659 -0.27188716 -0.36348917 -0.44813137 -0.52378993 -0.58933990 -0.64452081 -0.68976588 -0.72597059 -0.75426758 -0.77584792 -0.79184106 -0.80324796 -0.81091373 -0.81552561 -0.81762451 -0.81762203 -0.81581795 -0.81241527 -0.80753152 -0.80120567 -0.79340058 -0.78400082 -0.77280618 -0.75952120 -0.74374178 -0.72494076 -0.70245642 -0.67549031 -0.64312460 -0.60437232 -0.55827551 -0.50406169 -0.44135418 -0.37040455 -0.29228246 -0.20893746 -0.12306461 -0.03776978 0.04388311 0.11930467 0.18666695 0.24499002 0.29405451 0.33421310 0.36617718 0.39083036 0.40909138 0.42182759 0.42980943 0.43369379 0.43402538 0.43124846 0.42572368 0.41774708 0.40756973 0.39541694 0.38150660 0.36606574 0.34934458 0.33162691 0.31323553 0.29453199 0.27591008 0.25778343 0.24056869 0.22466606 0.21043961 0.19819948 0.18818774 0.18056849 0.17542239 0.17274513 0.17244906 0.17436764 0.17826226 0.18383178 0.19072493 0.19855582 0.20692215 0.21542529 0.22369041 0.23138456 0.23823070 0.24401596 0.24859375 0.25187975 0.25384341 0.25449641 0.25387986 0.25205187 0.24907617 0.24501258 0.23990914 0.23379591 0.22668001 0.21854169 0.20933136 0.19896779 0.18733824 0.17430194 0.15969916 0.14336899 0.12517912 0.10507001 0.08311183 0.05956525 0.03492731 0.00993632 -0.01448674 -0.03736218 -0.05781116 -0.07519836 -0.08920969 -0.09984736 -0.10736068 -0.11214909 -0.11467085 -0.11537606 -0.11466736 -0.11288331 -0.11029675 -0.10712104 -0.10351953 -0.09961537 -0.09550034 -0.09124204 -0.08688970 -0.08247850 -0.07803284 -0.07356880 -0.06909595 -0.06461879 -0.06013803 -0.05565184 -0.05115734 -0.04665239 -0.04213800 -0.03762114 -0.03311802 -0.02865727 -0.02428214 -0.02005088 -0.01603410 -0.01230868 -0.00894888 -0.00601627 -0.00355097 -0.00156654 -0.00004953 0.00103669 0.00174532 0.00213868 0.00228156 0.00223608 0.00205847 0.00179728 0.00149290 0.00117769 0.00087655 0.00060761 0.00038302 0.00020960 0.00008958 0.00002130 0.00000000

***THE CODE FOR THE LOW PASS FILTERS:

% % [b a] = iirdes3614(n, w, f, fs) % % Design an nth-order infinite impulse response (IIR) Butterworth filter % with a given bandwidth 'w', center frequency 'f', and sampling % frequency 'fs'. % % For a low pass filter, set 'f' to 0 and 'w' to the desired bandwidth. % For a bandpass filter, set 'f' to the center frequency and 'w' to the % desired bandwidth. % % To use the filter, use the Matlab/Octave filter function % y = filter(b,a,x), where b and a are the filter coefficients computed % by this function, x is the signal to be filtered, and y is the output. % % For example, the following designs a 3rd-order butterworth bandpass % filter with a bandwidth of 20 Hz centered at 100 Hz assuming a sample % rate of 800 Hz, and then plots the frequency response. % % order = 3; % bandwidth = 20; % fc = 100; % fs = 800; % [b a] = iirdes3614(order, bandwidth, fc, fs); % freqz(b,a,1024,fs); %

function [b a] = iirdes3614(n, w, f, fs)

if nargin

if n fs/2, error('bandwidth cannot exceed fs/2'); elseif f > fs/2, error('center frequency cannot exceed fs/2'); end;

% filter type if f==0, type = 'lowpass'; fc = w / fs; % cut-off frequency f0 = 0.0; % center frequency else type = 'bandpass'; fc = (f-0.5*w)/fs; % cut-off frequency f0 = f / fs; % center frequency end;

% filter order parameters r = mod(n,2); % odd filter? L = (n-r)/2; % filter semi-length

% compute analog zeros/poles/gain za = []; % analog zeros pa = []; % analog poles ka = 1; % analog gain for i=0:L-1, theta = ( 2*(i+1) + n - 1 ) * pi / (2*n); pa(end+1) = exp( j*theta); pa(end+1) = exp(-j*theta); end; if r, pa(end+1) = -1; end;

% frequency pre-warp if strcmp(type,'lowpass'), m = tan(pi*fc); elseif strcmp(type,'bandpass'), m = (cos(2*pi*fc) - cos(2*pi*f0) ) / sin(2*pi*fc); else, error(['invalid type: ' type]); end; m = abs(m);

% bilinear z-transform zd = []; % digital zeros pd = []; % digital poles kd = ka; % digital gain for i=1:length(pa), % compute digital zeros (pad with -1s) if i

% compute digital poles pd(i) = (1 + pa(i)*m) / (1 - pa(i)*m);

% update digital gain kd = kd * (1 - pd(i)) / (1 - zd(i)); end;

% transform to band-pass if necessary if strcmp(type,'bandpass'), zdt = zeros(1,2*n); % transformed digital zeros pdt = zeros(1,2*n); % transformed digital poles c0 = cos(2*pi*f0); for i=0:(n-1), t0 = 1 + zd(i+1); zdt(2*i+1) = 0.5*( c0*t0 + sqrt(c0^2*t0^2 - 4*zd(i+1)) ); zdt(2*i+2) = 0.5*( c0*t0 - sqrt(c0^2*t0^2 - 4*zd(i+1)) );

t0 = 1 + pd(i+1); pdt(2*i+1) = 0.5*( c0*t0 + sqrt(c0^2*t0^2 - 4*pd(i+1)) ); pdt(2*i+2) = 0.5*( c0*t0 - sqrt(c0^2*t0^2 - 4*pd(i+1)) ); end;

% overwrite old digital poles and zeros zd = zdt; pd = pdt;

% update order to reflect change n = 2*n; end;

% expand numerator and denominator b = 1; a = 1; for i=1:n, b = conv(b, [1, -zd(i)]); a = conv(a, [1, -pd(i)]); end; b = real( b * kd ); a = real( a );

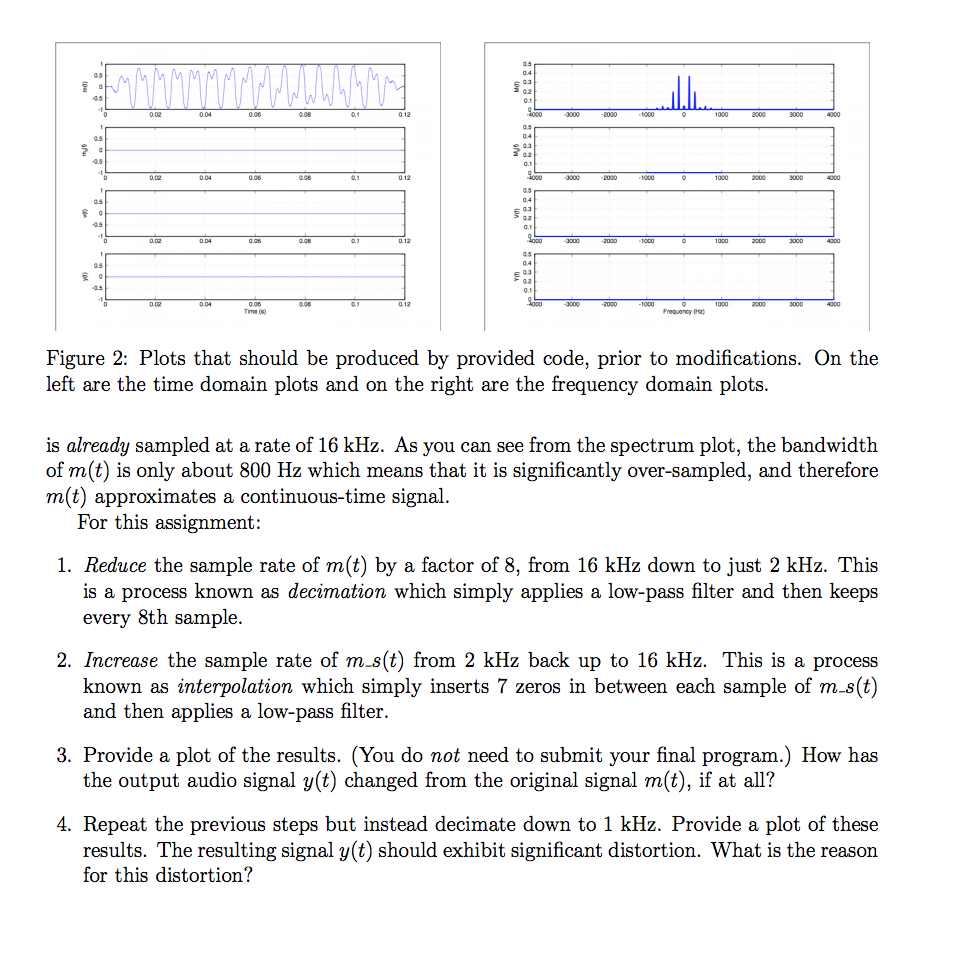
For this assignment you will need to obtain a copy of MATLAB or GNU Octave and sam ple and reconstruct an audio signa. which can be downloaded from the Files section of the course website on Canvas, in the Miniprojects folder. The program is named sampling.m and simulates the system shown in Figure 1. or your convenience, a basic program is provided, decimator m(t) input fs = 16 kHz LPF sampled y(t), output, v(t) LPF 16 kHz nterpolator Figure 1: Block diagram of simulated system For this assignment, you will need the following three files, which are all in the Miniprojects folder of the Files section of the course website on Canvas: sampling.m: The main MATLAB script that you need to modify for this assignment audio, dat: A plain text data file representing the audio signal to be processed iirde s3614. m: A useful function for designing low-pass filters. Run help irdes36 14 on the Matlab or GNU Octave command line for help. A good value for the filter order Running the sampling.m program without any modification should produce two plots The purpose of this assignment is to help you understand the process of sampling an is similar to these. analog signal. However, because we are working on a computer, the input audio signal m(t) For this assignment you will need to obtain a copy of MATLAB or GNU Octave and sam ple and reconstruct an audio signa. which can be downloaded from the Files section of the course website on Canvas, in the Miniprojects folder. The program is named sampling.m and simulates the system shown in Figure 1. or your convenience, a basic program is provided, decimator m(t) input fs = 16 kHz LPF sampled y(t), output, v(t) LPF 16 kHz nterpolator Figure 1: Block diagram of simulated system For this assignment, you will need the following three files, which are all in the Miniprojects folder of the Files section of the course website on Canvas: sampling.m: The main MATLAB script that you need to modify for this assignment audio, dat: A plain text data file representing the audio signal to be processed iirde s3614. m: A useful function for designing low-pass filters. Run help irdes36 14 on the Matlab or GNU Octave command line for help. A good value for the filter order Running the sampling.m program without any modification should produce two plots The purpose of this assignment is to help you understand the process of sampling an is similar to these. analog signal. However, because we are working on a computer, the input audio signal m(t)