Answered step by step
Verified Expert Solution
Question
1 Approved Answer
The sequence {a_(n)} is defined by a_(1)=2 , and a_(n+1)=(1)/(2)(a_(n)+(2)/(a_(n))) for n>=1 . Assuming that {a_(n)} converges, find its limit. lim_(n->infty )a_(n)= Hint:
The sequence
{a_(n)}is defined by
a_(1)=2, and\
a_(n+1)=(1)/(2)(a_(n)+(2)/(a_(n)))\ for
n>=1. Assuming that
{a_(n)}converges, find its limit.\
\\\\lim_(n->\\\\infty )a_(n)=\ Hint: Let
a=\\\\lim_(n->\\\\infty )a_(n). Then, since
a_(n+1)=(1)/(2)(a_(n)+(2)/(a_(n))), we have
a=(1)/(2)(a+(2)/(a)). Now solve for
a.
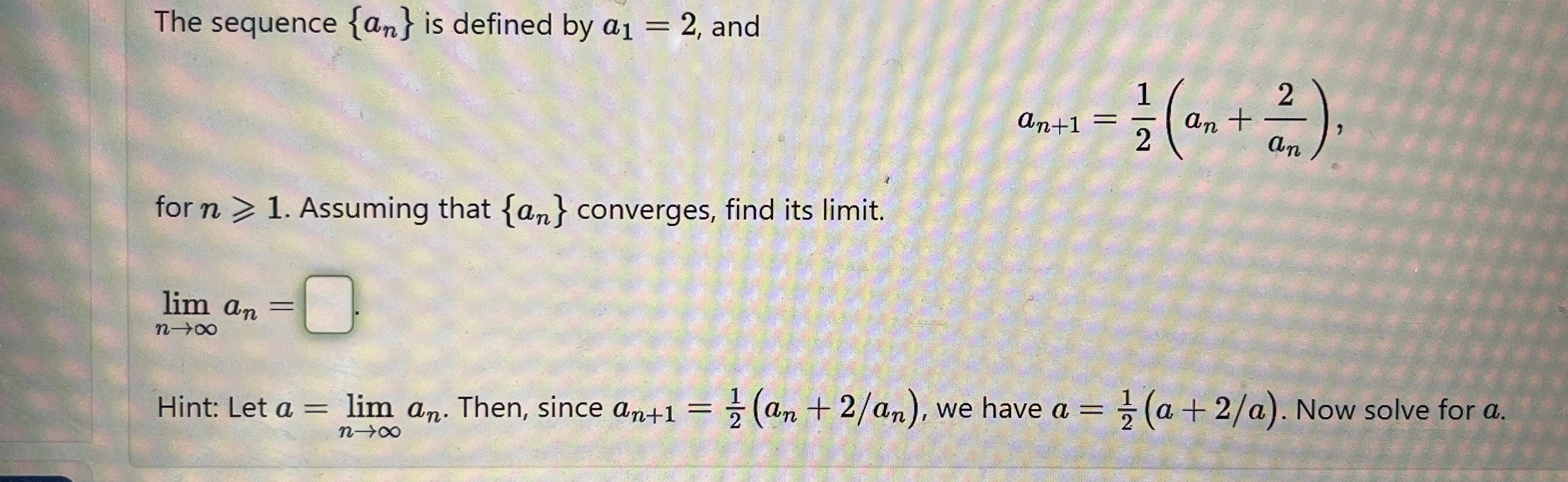
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


