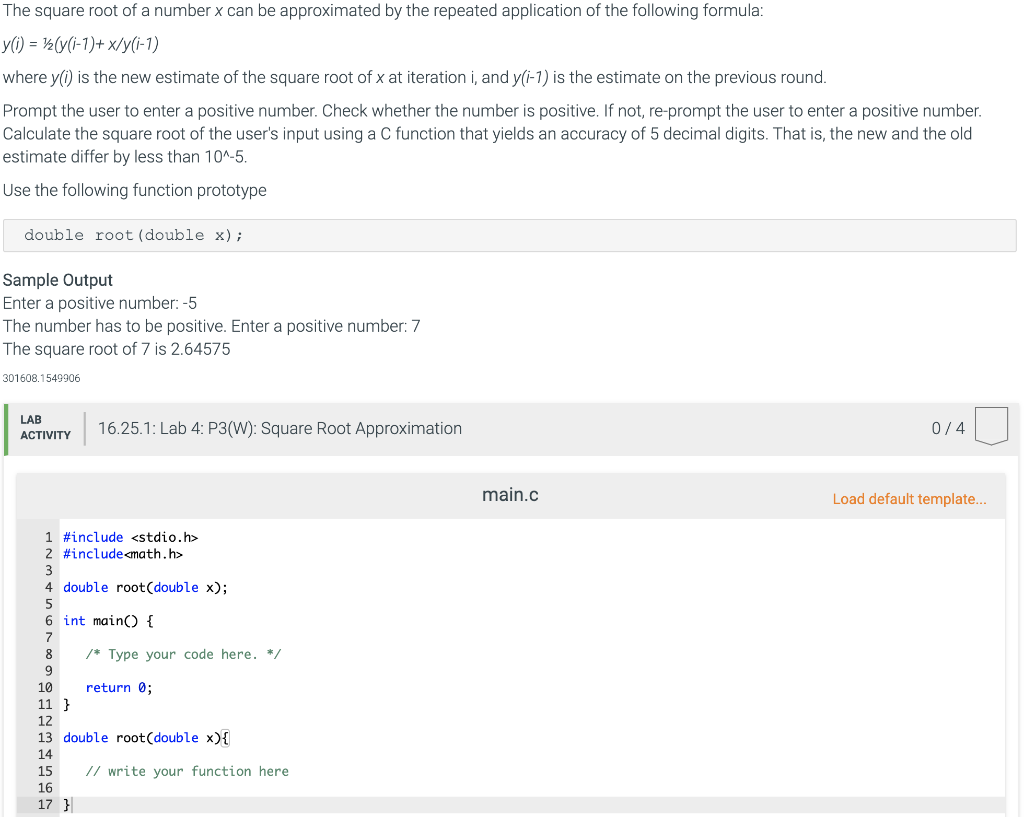
Question
The square root of a number x can be approximated by the repeated application of the following formula: y(i) = (y(i-1)+ x/y(i-1) where y(i) is
The square root of a number x can be approximated by the repeated application of the following formula:
y(i) = (y(i-1)+ x/y(i-1)
where y(i) is the new estimate of the square root of x at iteration i, and y(i-1) is the estimate on the previous round.
Prompt the user to enter a positive number. Check whether the number is positive. If not, re-prompt the user to enter a positive number. Calculate the square root of the user's input using a C function that yields an accuracy of 5 decimal digits. That is, the new and the old estimate differ by less than 10^-5.
Use the following function prototype
double root(double x);
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


