Answered step by step
Verified Expert Solution
Question
1 Approved Answer
The STD of the portfolio is: 0.0297 0.021 0.0241 0.0384 none of the above begin{tabular}{|c|c|c|c|c|c|c|c|} hline & L & M & N & 0 &
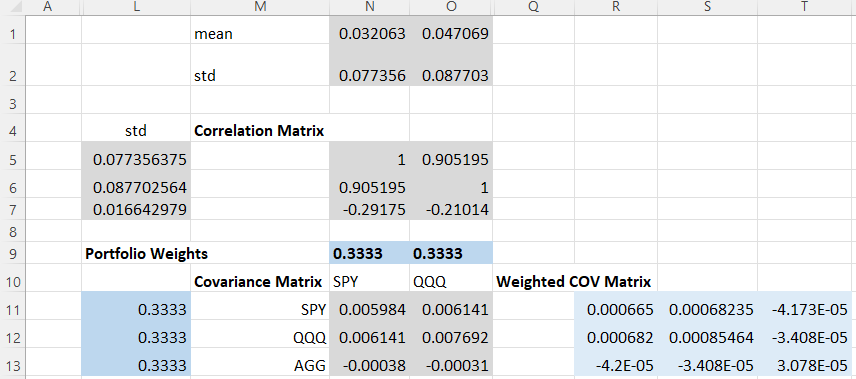

The STD of the portfolio is:
- 0.0297
- 0.021
- 0.0241
- 0.0384
- none of the above
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


