Question
The top 5 stocks in the S&P 500 index, when ranked by market capitalization, make up 22% of the total market capitalization of the S&P
The top 5 stocks in the S&P 500 index, when ranked by market capitalization, make up 22% of the total market capitalization of the S&P 500 index.
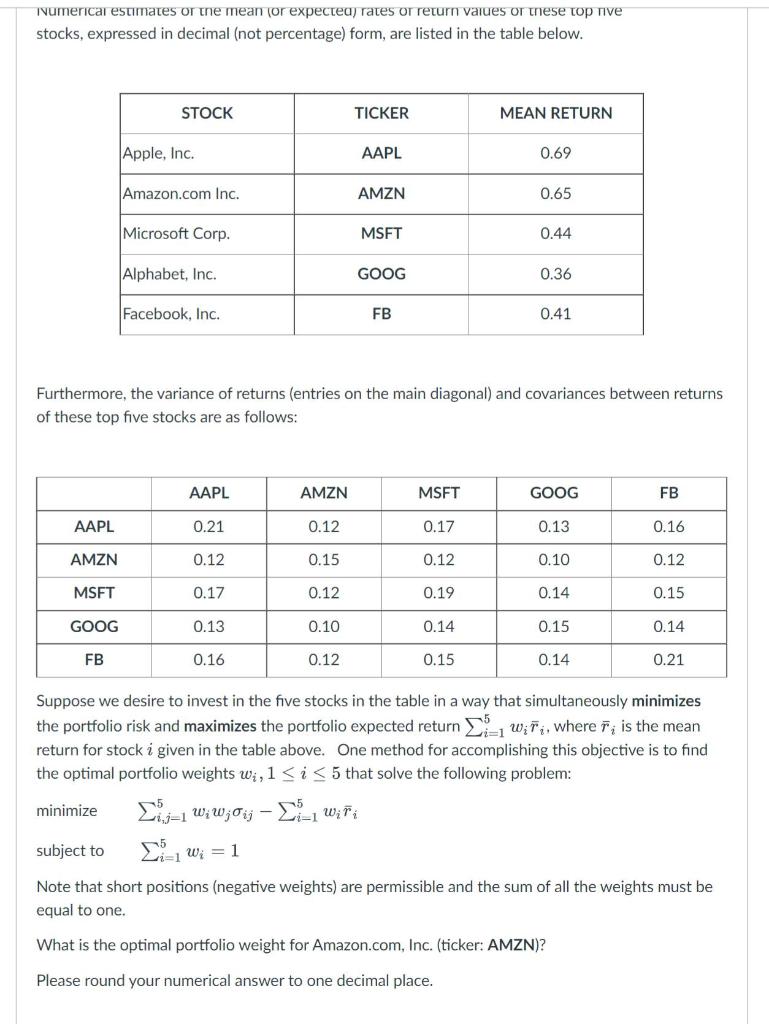
Numerical estimates of the mean (or expected) rates of return values of these top five stocks, expressed in decimal (not percentage) form, are listed in the table below.
| STOCK | TICKER | MEAN RETURN |
| Apple, Inc. | AAPL | 0.69 |
| Amazon.com Inc. | AMZN | 0.65 |
| Microsoft Corp. | MSFT | 0.44 |
| Alphabet, Inc. | GOOG | 0.36 |
| Facebook, Inc. | FB | 0.41 |
Furthermore, the variance of returns (entries on the main diagonal) and covariances between returns of these top five stocks are as follows:
|
| AAPL | AMZN | MSFT | GOOG | FB |
| AAPL | 0.21 | 0.12 | 0.17 | 0.13 | 0.16 |
| AMZN | 0.12 | 0.15 | 0.12 | 0.10 | 0.12 |
| MSFT | 0.17 | 0.12 | 0.19 | 0.14 | 0.15 |
| GOOG | 0.13 | 0.10 | 0.14 | 0.15 | 0.14 |
| FB | 0.16 | 0.12 | 0.15 | 0.14 | 0.21 |
Suppose we desire to invest in the five stocks in the table in a way that simultaneously minimizes the portfolio risk and maximizes the portfolio expected return where r_bar, is the mean return for stock i given in the table above. One method for accomplishing this objective is to find the optimal portfolio weights wi, 1
Minimize
Subject to
Note that short positions (negative weights) are permissible and the sum of all the weights must be equal to one.
What is the optimal portfolio weight for Amazon.com, Inc.
Round to 2 decimal place
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


