The very last picture is the Excel spreadsheet, all I want to know are the formulas that I need to use.

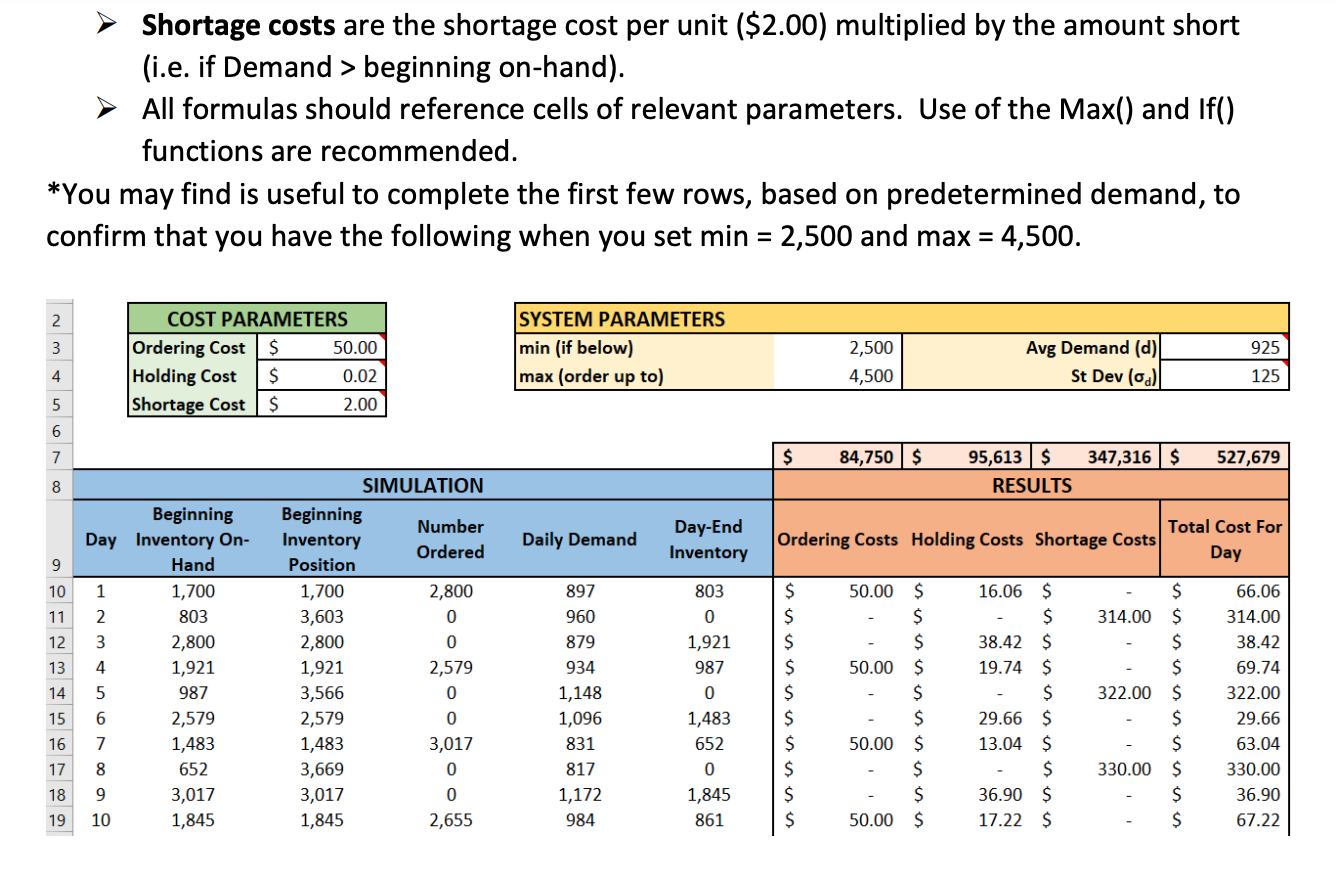
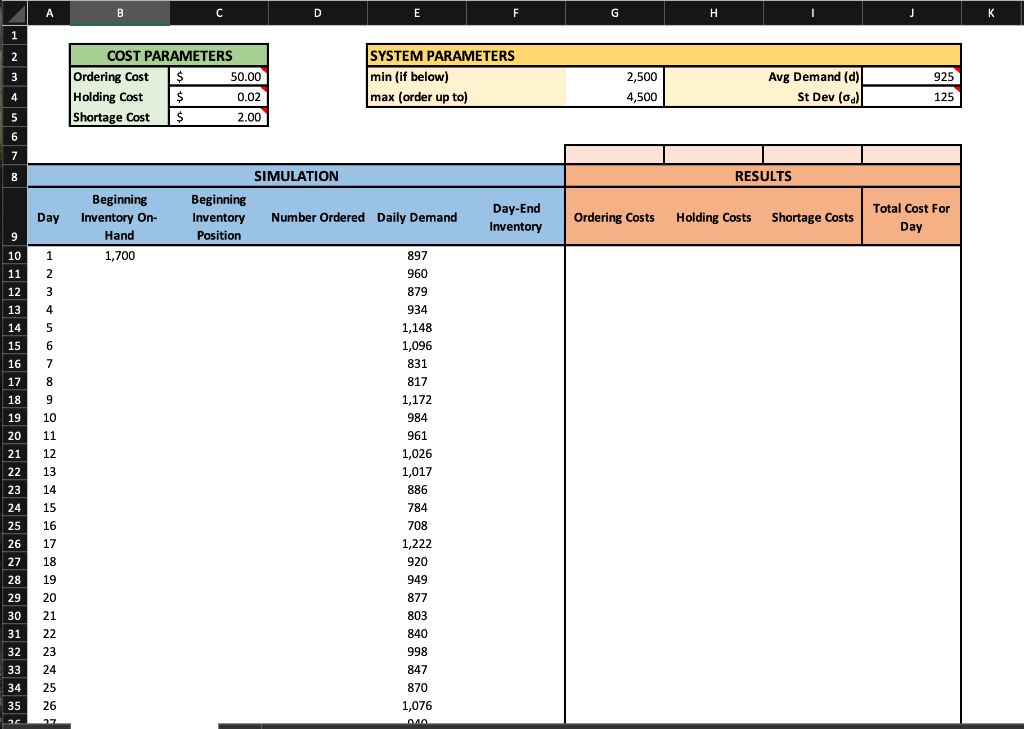
Inventory Simulation: An optional replenishment inventory system (also called a min/max system) is one in which inventory position is reviewed periodically and an order is in placed in a predetermined amount (min). The amount ordered will be the quantity needed to bring inventory position up to a predetermined amount (max). Inventory position equals inventory on hand plus inventory on order, less any backorders if applicable (we don't use backorders in this exercise). We will simulate the model described above for 5,000 days with a given average and standard deviation of daily demand. Additional information is as follows: assume that inventory position is reviewed at the start of each day, the order lead time is two days (i.e. orders arrive at the start of the day two days after being placed), and any demand not met is considered a lost sale (i.e. there are no backorders). Complete the model provided in the Excel workbook to implement the inventory system described above. This will require that you develop formulas in the cells of the model to reflect the inventory policy described and calculate total costs. Use the following as a guide: Beginning inventory on-hand equals the previous days Day-end inventory plus any arriving order (i.e. ordered two days previous). Beginning inventory position is equal to beginning inventory on-hand plus any outstanding orders that have yet to arrive. Number ordered will contain an If() statement - if beginning inventory position is less than min, order enough to bring it up to max (i.e. order max minus beginning inventory position). Day-end inventory is beginning inventory on-hand minus daily demand. (Note: can not be less than zero). Ordering costs are the cost per order ($50) if an order is placed on that day (i.e. if the "Number ordered" cell is greater than zero). Holding costs are calculated each day based on a per-piece per-day cost ($0.02) multiplied by the ending inventory for that day. Shortage costs are the shortage cost per unit (\$2.00) multiplied by the amount short (i.e. if Demand > beginning on-hand). All formulas should reference cells of relevant parameters. Use of the Max() and If() functions are recommended. You may find is useful to complete the first few rows, based on predetermined demand, to onfirm that you have the following when you set min=2,500 and max=4,500. What do you think will happen to total ordering, holding and shortage costs as min and max are changed? For each of the following, make a hypothesis before using the simulation to test. 1. If min remains at 2,500 while max is increased, a. Total ordering costs will (increase/decrease) b. Total holding costs will (increase/decrease) c. Total shortage costs will (increase/decrease) d. Test your hypothesis by leaving min=2,500 and changing max to 5,000. Were your correct? Try, in your own words, to explain the reasons. 2. Set max to 4,500 again. What do you think will happen if max remains at 4,500 while min is increased? a. Total ordering costs will (increase/decrease) b. Total holding costs will (increase/decrease) c. Total shortage costs will (increase/decrease) d. Test your hypothesis by leaving max=4,500 and changing min to 3,000. Were your correct? 3. Experiment with different values of min and max and see how low you can get total costs. (Hint - Try to get total costs down to about \$230,000). 4. [Time permitting]. Make a copy of your model worksheet. Modify the model to reflect a three (rather than two) day lead time. \begin{tabular}{|lr|r|r|} \hline SYSTEM PARAMETERS \\ \hline min (if below) & 2,500 & \multicolumn{5}{l|}{} \\ max (order up to) & 4,500 & Avg Demand (d) & 925 \\ \cline { 1 - 4 } & & St Dev ( d) & 125 \\ \hline \end{tabular} Inventory Simulation: An optional replenishment inventory system (also called a min/max system) is one in which inventory position is reviewed periodically and an order is in placed in a predetermined amount (min). The amount ordered will be the quantity needed to bring inventory position up to a predetermined amount (max). Inventory position equals inventory on hand plus inventory on order, less any backorders if applicable (we don't use backorders in this exercise). We will simulate the model described above for 5,000 days with a given average and standard deviation of daily demand. Additional information is as follows: assume that inventory position is reviewed at the start of each day, the order lead time is two days (i.e. orders arrive at the start of the day two days after being placed), and any demand not met is considered a lost sale (i.e. there are no backorders). Complete the model provided in the Excel workbook to implement the inventory system described above. This will require that you develop formulas in the cells of the model to reflect the inventory policy described and calculate total costs. Use the following as a guide: Beginning inventory on-hand equals the previous days Day-end inventory plus any arriving order (i.e. ordered two days previous). Beginning inventory position is equal to beginning inventory on-hand plus any outstanding orders that have yet to arrive. Number ordered will contain an If() statement - if beginning inventory position is less than min, order enough to bring it up to max (i.e. order max minus beginning inventory position). Day-end inventory is beginning inventory on-hand minus daily demand. (Note: can not be less than zero). Ordering costs are the cost per order ($50) if an order is placed on that day (i.e. if the "Number ordered" cell is greater than zero). Holding costs are calculated each day based on a per-piece per-day cost ($0.02) multiplied by the ending inventory for that day. Shortage costs are the shortage cost per unit (\$2.00) multiplied by the amount short (i.e. if Demand > beginning on-hand). All formulas should reference cells of relevant parameters. Use of the Max() and If() functions are recommended. You may find is useful to complete the first few rows, based on predetermined demand, to onfirm that you have the following when you set min=2,500 and max=4,500. What do you think will happen to total ordering, holding and shortage costs as min and max are changed? For each of the following, make a hypothesis before using the simulation to test. 1. If min remains at 2,500 while max is increased, a. Total ordering costs will (increase/decrease) b. Total holding costs will (increase/decrease) c. Total shortage costs will (increase/decrease) d. Test your hypothesis by leaving min=2,500 and changing max to 5,000. Were your correct? Try, in your own words, to explain the reasons. 2. Set max to 4,500 again. What do you think will happen if max remains at 4,500 while min is increased? a. Total ordering costs will (increase/decrease) b. Total holding costs will (increase/decrease) c. Total shortage costs will (increase/decrease) d. Test your hypothesis by leaving max=4,500 and changing min to 3,000. Were your correct? 3. Experiment with different values of min and max and see how low you can get total costs. (Hint - Try to get total costs down to about \$230,000). 4. [Time permitting]. Make a copy of your model worksheet. Modify the model to reflect a three (rather than two) day lead time. \begin{tabular}{|lr|r|r|} \hline SYSTEM PARAMETERS \\ \hline min (if below) & 2,500 & \multicolumn{5}{l|}{} \\ max (order up to) & 4,500 & Avg Demand (d) & 925 \\ \cline { 1 - 4 } & & St Dev ( d) & 125 \\ \hline \end{tabular}