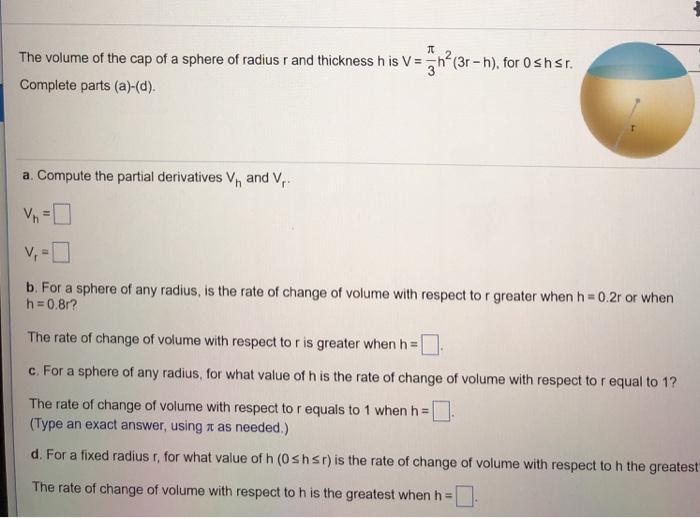
The volume of the cap of a sphere of radius r and thickness h is V = h (3r - h), for 0 shsr. Complete parts (a)-(d). a. Compute the partial derivatives Vn and V,. V = %3D V, -O b. For a sphere of any radius, is the rate of change of volume with respect to r greater whenh 0.2r or when h=0.8r? The rate of change of volume with respect to r is greater when h = c. For a sphere of any radius, for what value of h is the rate of change of volume with respect to r equal to 1? The rate of change of volume with respect to r equals to 1 when h = (Type an exact answer, using x as needed.) d. For a fixed radius r, for what value of h (0shsr) is the rate of change of volume with respect to h the greatest The rate of change of volume with respect to h is the greatest when h =